
Question Number 69623 by aliesam last updated on 25/Sep/19
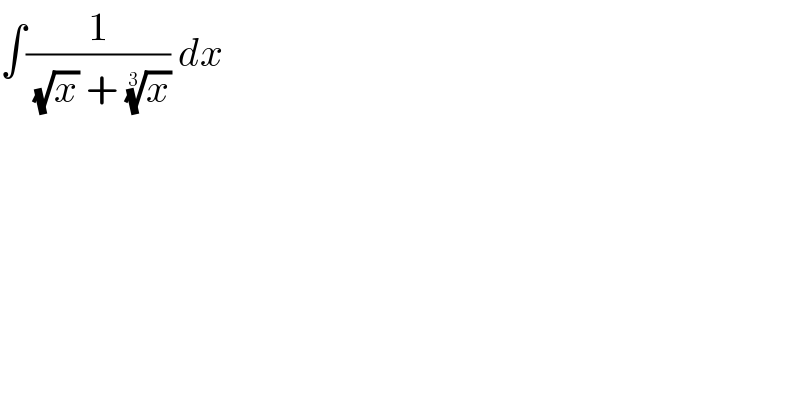
$$\int\frac{\mathrm{1}}{\sqrt{{x}}\:+\:\sqrt[{\mathrm{3}}]{{x}}}\:{dx} \\ $$
Answered by MJS last updated on 25/Sep/19
![we had this before... ∫(dx/(x^(1/2) +x^(1/3) ))= [t=x^(1/6) → dx=6x^(5/6) dt] =6∫(t^3 /(t+1))dt=6∫(t^2 −t+1−(1/(t+1)))dt= =2t^3 −3t^2 +6t−6ln (t+1) = =2x^(1/2) −3x^(1/3) +6x^(1/6) −6ln (x^(1/6) +1) +C](Q69629.png)
$$\mathrm{we}\:\mathrm{had}\:\mathrm{this}\:\mathrm{before}... \\ $$$$\int\frac{{dx}}{{x}^{\mathrm{1}/\mathrm{2}} +{x}^{\mathrm{1}/\mathrm{3}} }= \\ $$$$\:\:\:\:\:\left[{t}={x}^{\mathrm{1}/\mathrm{6}} \:\rightarrow\:{dx}=\mathrm{6}{x}^{\mathrm{5}/\mathrm{6}} {dt}\right] \\ $$$$=\mathrm{6}\int\frac{{t}^{\mathrm{3}} }{{t}+\mathrm{1}}{dt}=\mathrm{6}\int\left({t}^{\mathrm{2}} −{t}+\mathrm{1}−\frac{\mathrm{1}}{{t}+\mathrm{1}}\right){dt}= \\ $$$$=\mathrm{2}{t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} +\mathrm{6}{t}−\mathrm{6ln}\:\left({t}+\mathrm{1}\right)\:= \\ $$$$=\mathrm{2}{x}^{\mathrm{1}/\mathrm{2}} −\mathrm{3}{x}^{\mathrm{1}/\mathrm{3}} +\mathrm{6}{x}^{\mathrm{1}/\mathrm{6}} −\mathrm{6ln}\:\left({x}^{\mathrm{1}/\mathrm{6}} +\mathrm{1}\right)\:+{C} \\ $$
