
Question Number 92949 by Ar Brandon last updated on 09/May/20
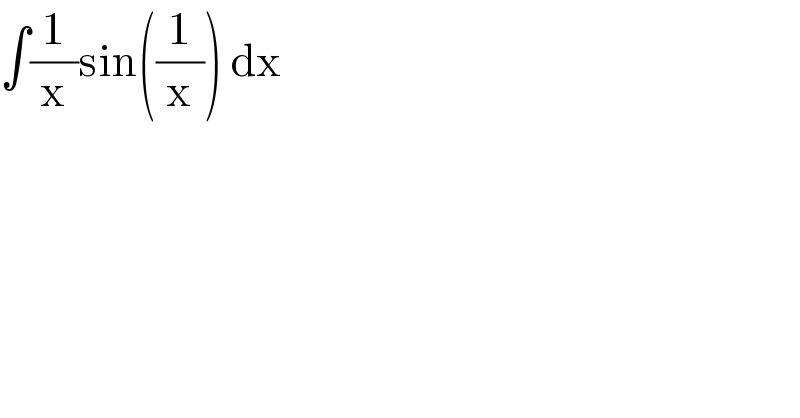
$$\int\frac{\mathrm{1}}{\mathrm{x}}\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:\mathrm{dx} \\ $$
Commented by mathmax by abdo last updated on 10/May/20
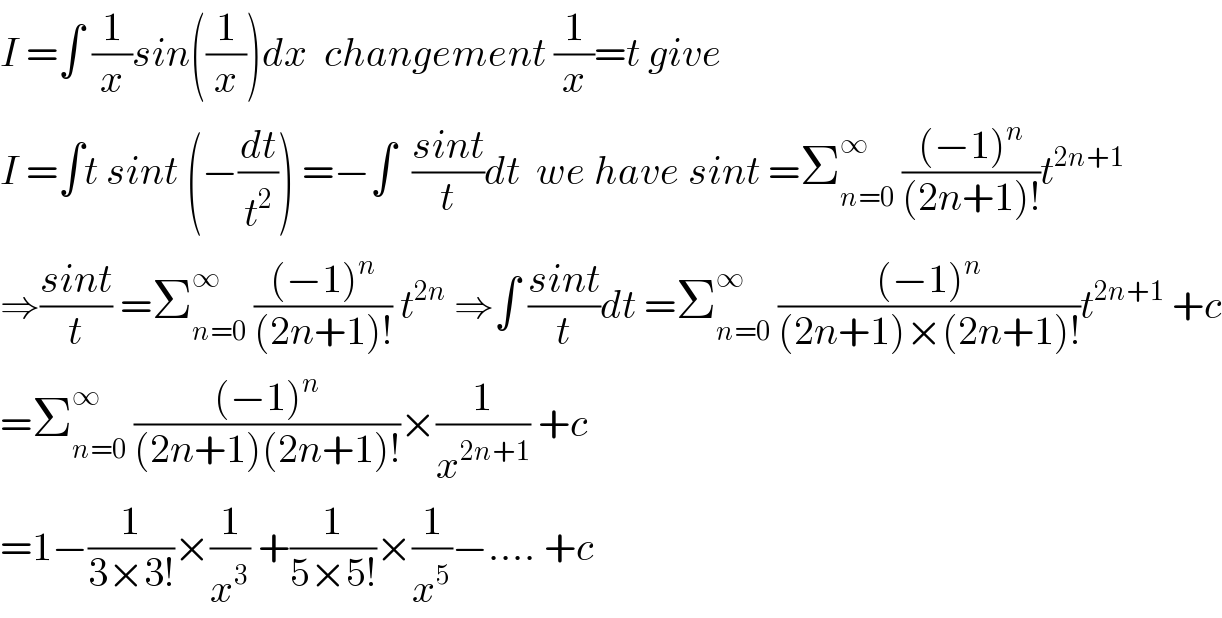
$${I}\:=\int\:\frac{\mathrm{1}}{{x}}{sin}\left(\frac{\mathrm{1}}{{x}}\right){dx}\:\:{changement}\:\frac{\mathrm{1}}{{x}}={t}\:{give} \\ $$$${I}\:=\int{t}\:{sint}\:\left(−\frac{{dt}}{{t}^{\mathrm{2}} }\right)\:=−\int\:\:\frac{{sint}}{{t}}{dt}\:\:{we}\:{have}\:{sint}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}{t}^{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\Rightarrow\frac{{sint}}{{t}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:{t}^{\mathrm{2}{n}} \:\Rightarrow\int\:\frac{{sint}}{{t}}{dt}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)×\left(\mathrm{2}{n}+\mathrm{1}\right)!}{t}^{\mathrm{2}{n}+\mathrm{1}} \:+{c} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)!}×\frac{\mathrm{1}}{{x}^{\mathrm{2}{n}+\mathrm{1}} }\:+{c} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}×\mathrm{3}!}×\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\:+\frac{\mathrm{1}}{\mathrm{5}×\mathrm{5}!}×\frac{\mathrm{1}}{{x}^{\mathrm{5}} }−....\:+{c} \\ $$
Commented by mathmax by abdo last updated on 10/May/20
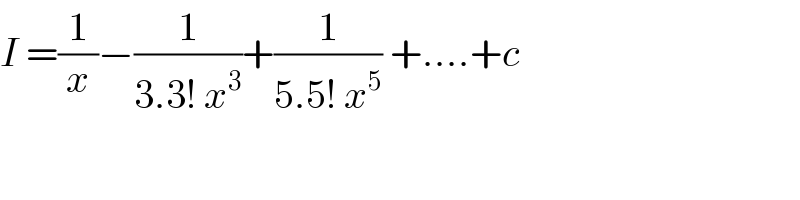
$${I}\:=\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\mathrm{3}.\mathrm{3}!\:{x}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{5}.\mathrm{5}!\:{x}^{\mathrm{5}} }\:+....+{c} \\ $$
Answered by peter frank last updated on 10/May/20
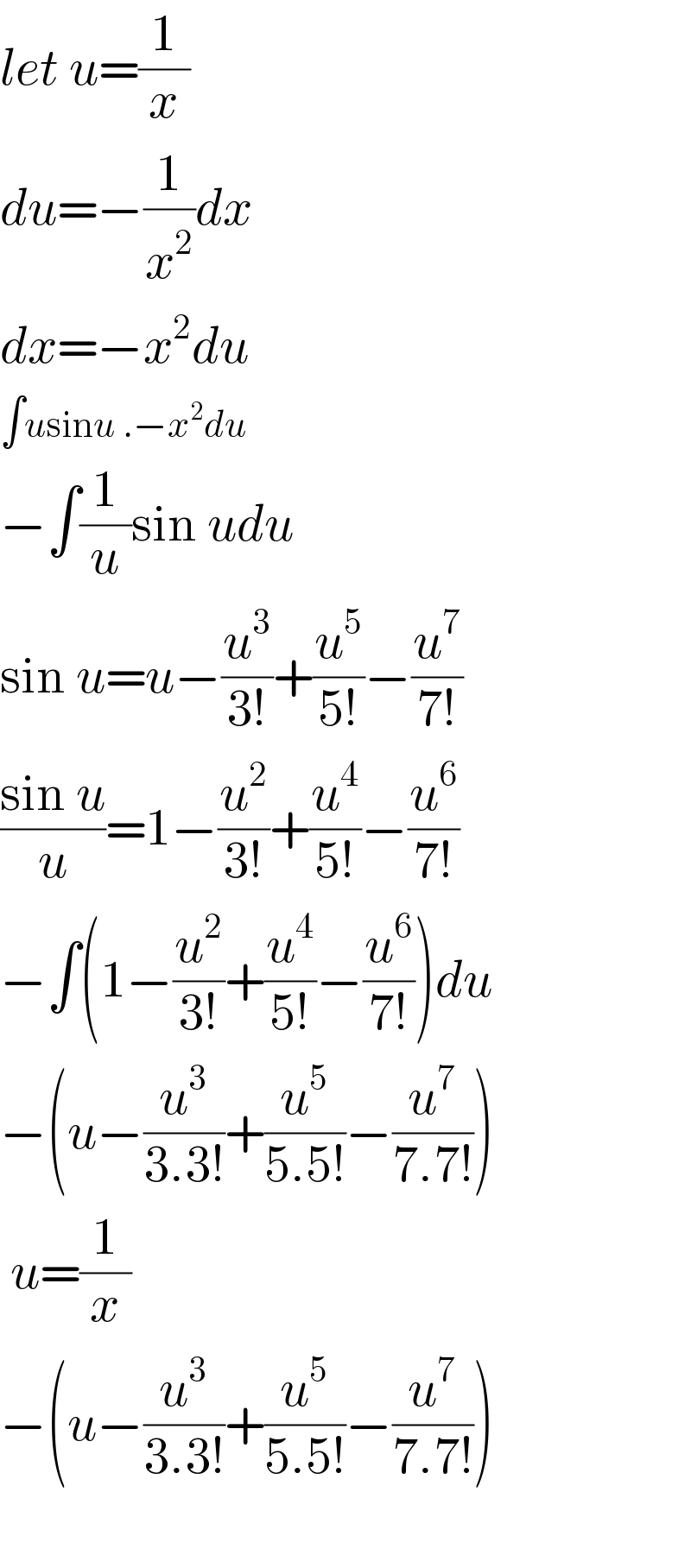
$${let}\:{u}=\frac{\mathrm{1}}{{x}} \\ $$$${du}=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx} \\ $$$${dx}=−{x}^{\mathrm{2}} {du} \\ $$$$\int{u}\mathrm{sin}{u}\:.−{x}^{\mathrm{2}} {du} \\ $$$$−\int\frac{\mathrm{1}}{{u}}\mathrm{sin}\:{udu} \\ $$$$\mathrm{sin}\:{u}={u}−\frac{{u}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{u}^{\mathrm{5}} }{\mathrm{5}!}−\frac{{u}^{\mathrm{7}} }{\mathrm{7}!} \\ $$$$\frac{\mathrm{sin}\:{u}}{{u}}=\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{3}!}+\frac{{u}^{\mathrm{4}} }{\mathrm{5}!}−\frac{{u}^{\mathrm{6}} }{\mathrm{7}!} \\ $$$$−\int\left(\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{3}!}+\frac{{u}^{\mathrm{4}} }{\mathrm{5}!}−\frac{{u}^{\mathrm{6}} }{\mathrm{7}!}\right){du} \\ $$$$−\left({u}−\frac{{u}^{\mathrm{3}} }{\mathrm{3}.\mathrm{3}!}+\frac{{u}^{\mathrm{5}} }{\mathrm{5}.\mathrm{5}!}−\frac{{u}^{\mathrm{7}} }{\mathrm{7}.\mathrm{7}!}\right) \\ $$$$\:{u}=\frac{\mathrm{1}}{{x}} \\ $$$$−\left({u}−\frac{{u}^{\mathrm{3}} }{\mathrm{3}.\mathrm{3}!}+\frac{{u}^{\mathrm{5}} }{\mathrm{5}.\mathrm{5}!}−\frac{{u}^{\mathrm{7}} }{\mathrm{7}.\mathrm{7}!}\right) \\ $$$$ \\ $$
