
Question Number 87881 by Rio Michael last updated on 06/Apr/20
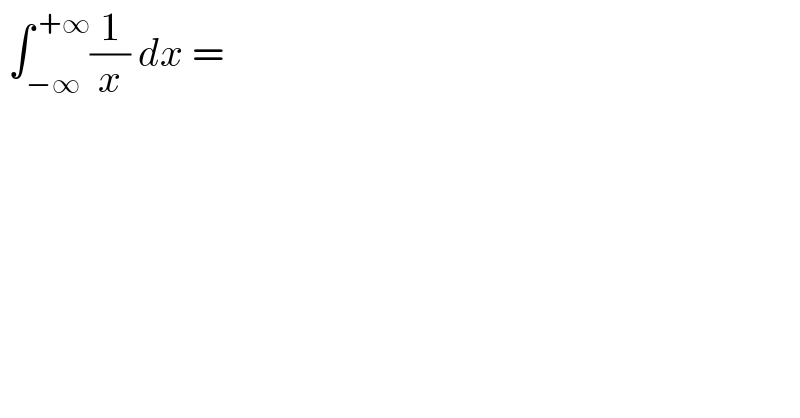
$$\:\int_{−\infty} ^{\:+\infty} \frac{\mathrm{1}}{{x}}\:{dx}\:=\: \\ $$
Commented by mathmax by abdo last updated on 06/Apr/20
![the function x→(1/x) is odd ⇒∫_(−∞) ^(+∞) (dx/x)=0 also we can write ∫_(−∞) ^(+∞) (dx/x) =lim_(ξ→+∞) ∫_(−ξ) ^ξ (dx/x) =lim_(ξ→+∞) [ln∣x∣]_(−ξ) ^ξ =0](Q87889.png)
$${the}\:{function}\:{x}\rightarrow\frac{\mathrm{1}}{{x}}\:{is}\:{odd}\:\Rightarrow\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}}=\mathrm{0}\: \\ $$$${also}\:{we}\:{can}\:{write}\:\:\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}}\:={lim}_{\xi\rightarrow+\infty} \:\:\int_{−\xi} ^{\xi} \:\frac{{dx}}{{x}} \\ $$$$={lim}_{\xi\rightarrow+\infty} \:\:\:\left[{ln}\mid{x}\mid\right]_{−\xi} ^{\xi} \:=\mathrm{0} \\ $$
Answered by mind is power last updated on 07/Apr/20

$${PV}\left(\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{{x}}{dx}\right)=\mathrm{0} \\ $$$${cauchy}\:\:{principal}\:{value} \\ $$$${but}\:\int_{−\infty} ^{\infty} \frac{{dx}}{{x}}\:{not}\:{exist}\:{Riemann} \\ $$
