Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 201110 by emilagazade last updated on 29/Nov/23

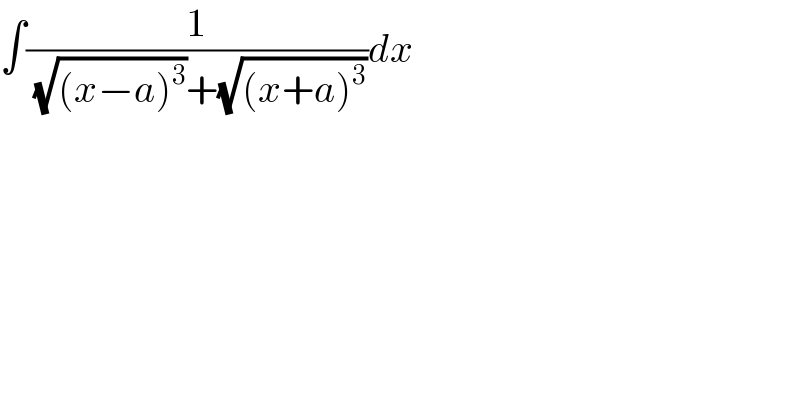
∫(1/( (√((x−a)^3 ))+(√((x+a)^3 ))))dx

$$\int\frac{\mathrm{1}}{\:\sqrt{\left({x}−{a}\right)^{\mathrm{3}} }+\sqrt{\left({x}+{a}\right)^{\mathrm{3}} }}{dx} \\ $$

Answered by Frix last updated on 29/Nov/23

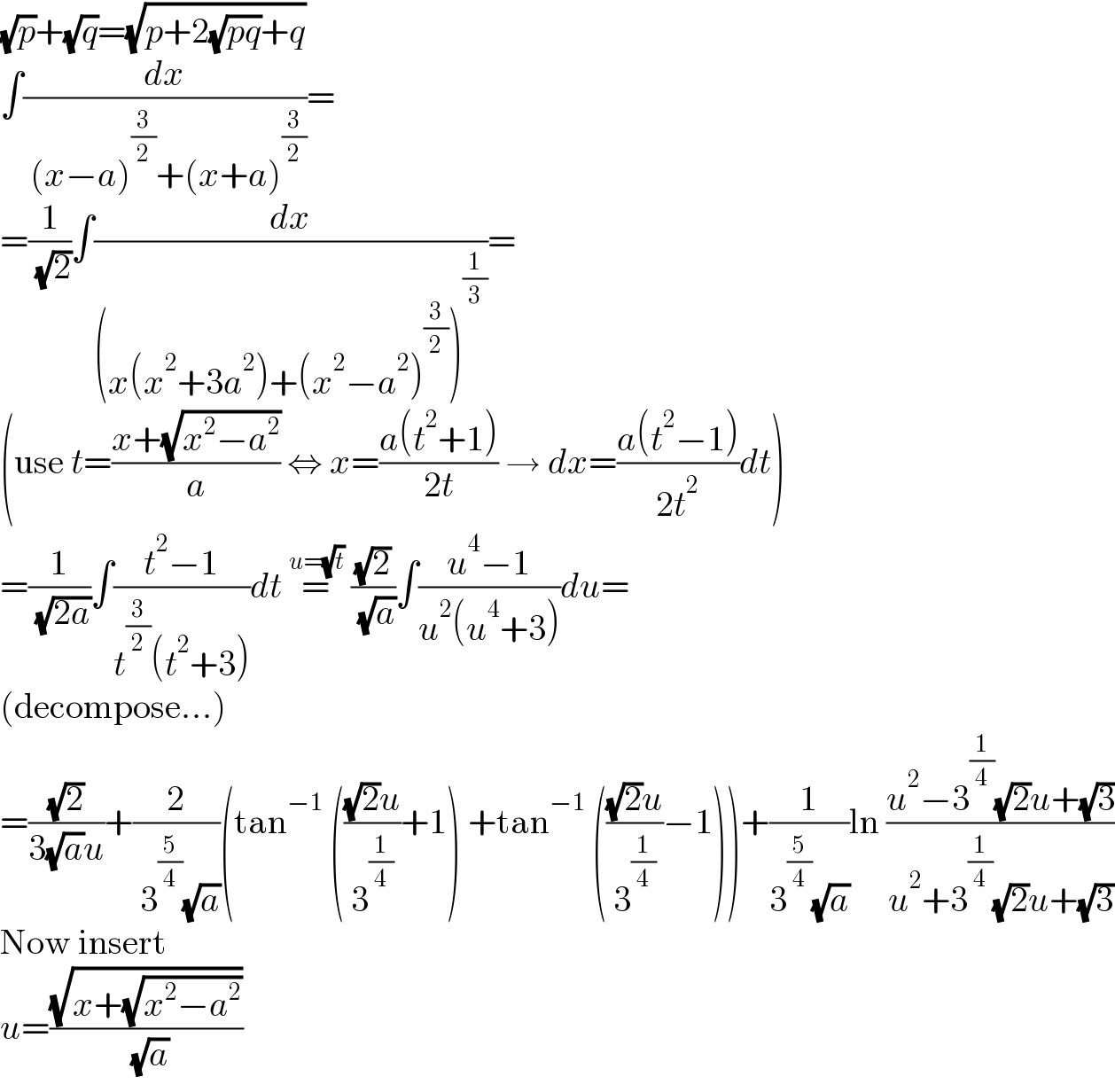
(√p)+(√q)=(√(p+2(√(pq))+q)) ∫(dx/( (x−a)^(3/2) +(x+a)^(3/2) ))= =(1/( (√2)))∫(dx/((x(x^2 +3a^2 )+(x^2 −a^2 )^(3/2) )^(1/3) ))= (use t=((x+(√(x^2 −a^2 )))/a) ⇔ x=((a(t^2 +1))/(2t)) → dx=((a(t^2 −1))/(2t^2 ))dt) =(1/( (√(2a))))∫((t^2 −1)/(t^(3/2) (t^2 +3)))dt =^(u=(√t)) ((√2)/( (√a)))∫((u^4 −1)/(u^2 (u^4 +3)))du= (decompose...) =((√2)/(3(√a)u))+(2/( 3^(5/4) (√a)))(tan^(−1) ((((√2)u)/3^(1/4) )+1) +tan^(−1) ((((√2)u)/3^(1/4) )−1))+(1/(3^(5/4) (√a)))ln ((u^2 −3^(1/4) (√2)u+(√3))/(u^2 +3^(1/4) (√2)u+(√3))) Now insert u=((√(x+(√(x^2 −a^2 ))))/( (√a)))

$$\sqrt{{p}}+\sqrt{{q}}=\sqrt{{p}+\mathrm{2}\sqrt{{pq}}+{q}} \\ $$$$\int\frac{{dx}}{\:\left({x}−{a}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\left({x}+{a}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }= \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{{dx}}{\left({x}\left({x}^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} \right)+\left({x}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} }= \\ $$$$\left(\mathrm{use}\:{t}=\frac{{x}+\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{{a}}\:\Leftrightarrow\:{x}=\frac{{a}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{2}{t}}\:\rightarrow\:{dx}=\frac{{a}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{2}{t}^{\mathrm{2}} }{dt}\right) \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{a}}}\int\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\frac{\mathrm{3}}{\mathrm{2}}} \left({t}^{\mathrm{2}} +\mathrm{3}\right)}{dt}\:\overset{{u}=\sqrt{{t}}} {=}\:\frac{\sqrt{\mathrm{2}}}{\:\sqrt{{a}}}\int\frac{{u}^{\mathrm{4}} −\mathrm{1}}{{u}^{\mathrm{2}} \left({u}^{\mathrm{4}} +\mathrm{3}\right)}{du}= \\ $$$$\left(\mathrm{decompose}...\right) \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{3}\sqrt{{a}}{u}}+\frac{\mathrm{2}}{\:\mathrm{3}^{\frac{\mathrm{5}}{\mathrm{4}}} \sqrt{{a}}}\left(\mathrm{tan}^{−\mathrm{1}} \:\left(\frac{\sqrt{\mathrm{2}}{u}}{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{4}}} }+\mathrm{1}\right)\:+\mathrm{tan}^{−\mathrm{1}} \:\left(\frac{\sqrt{\mathrm{2}}{u}}{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{4}}} }−\mathrm{1}\right)\right)+\frac{\mathrm{1}}{\mathrm{3}^{\frac{\mathrm{5}}{\mathrm{4}}} \sqrt{{a}}}\mathrm{ln}\:\frac{{u}^{\mathrm{2}} −\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{4}}} \sqrt{\mathrm{2}}{u}+\sqrt{\mathrm{3}}}{{u}^{\mathrm{2}} +\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{4}}} \sqrt{\mathrm{2}}{u}+\sqrt{\mathrm{3}}} \\ $$$$\mathrm{Now}\:\mathrm{insert} \\ $$$${u}=\frac{\sqrt{{x}+\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }}}{\:\sqrt{{a}}} \\ $$

Commented by emilagazade last updated on 29/Nov/23

thank you a lot Sir

$${thank}\:{you}\:{a}\:{lot}\:{Sir} \\ $$

Commented by Frix last updated on 29/Nov/23

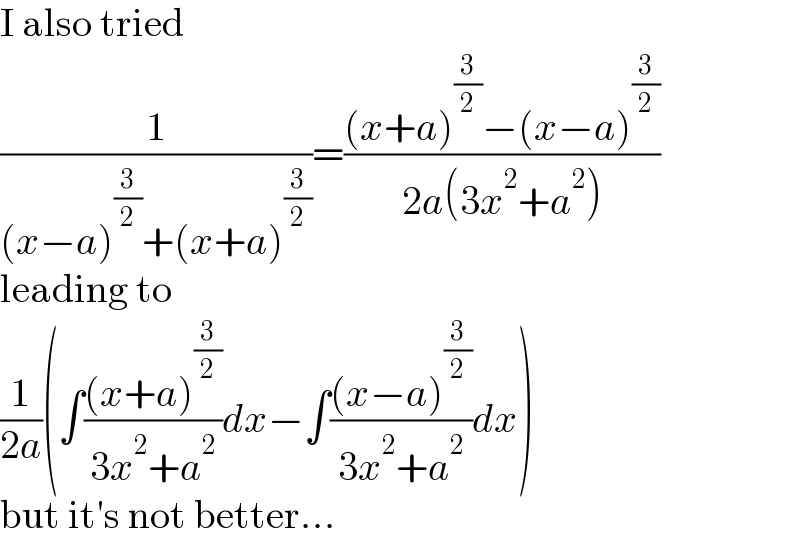
I also tried (1/((x−a)^(3/2) +(x+a)^(3/2) ))=(((x+a)^(3/2) −(x−a)^(3/2) )/(2a(3x^2 +a^2 ))) leading to (1/(2a))(∫(((x+a)^(3/2) )/(3x^2 +a^2 ))dx−∫(((x−a)^(3/2) )/(3x^2 +a^2 ))dx) but it′s not better...

$$\mathrm{I}\:\mathrm{also}\:\mathrm{tried} \\ $$$$\frac{\mathrm{1}}{\left({x}−{a}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\left({x}+{a}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }=\frac{\left({x}+{a}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\left({x}−{a}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{2}{a}\left(\mathrm{3}{x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)} \\ $$$$\mathrm{leading}\:\mathrm{to} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{a}}\left(\int\frac{\left({x}+{a}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3}{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }{dx}−\int\frac{\left({x}−{a}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3}{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }{dx}\right) \\ $$$$\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{better}... \\ $$

Commented by emilagazade last updated on 29/Nov/23

this one I tried too. but the book suggests to do substitution which leads to partial fractions.

$${this}\:{one}\:{I}\:{tried}\:{too}.\:{but}\:{the}\:{book}\:{suggests}\:{to}\:{do}\:{substitution}\:{which}\:{leads}\:{to}\:{partial}\:{fractions}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com