Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 127929 by mnjuly1970 last updated on 03/Jan/21

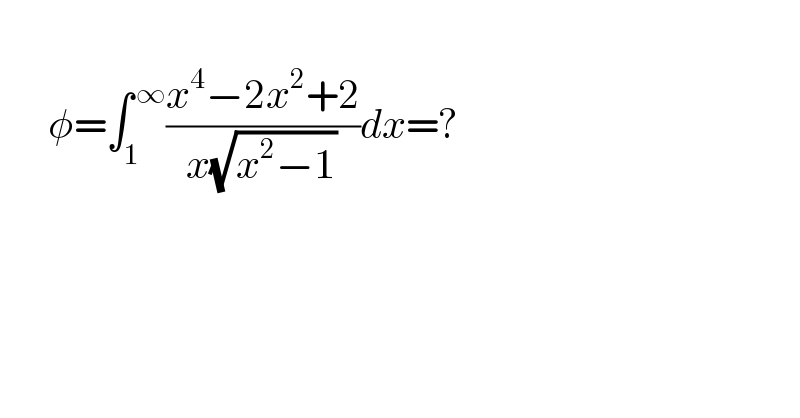
φ=∫_1 ^( ∞) ((x^4 −2x^2 +2)/(x(√(x^2 −1))))dx=?

$$ \\ $$$$\:\:\:\:\:\:\phi=\int_{\mathrm{1}} ^{\:\infty} \frac{{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}}{{x}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{dx}=? \\ $$

Answered by Ar Brandon last updated on 03/Jan/21

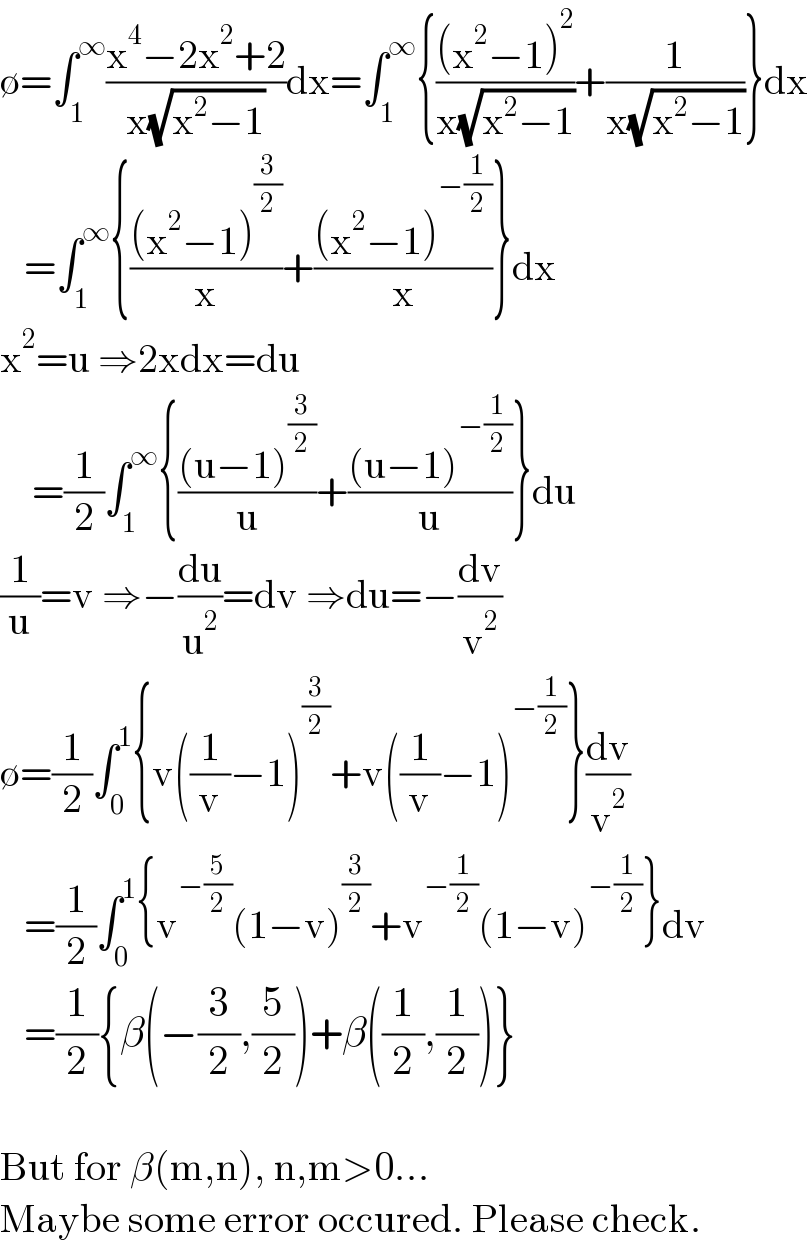
∅=∫_1 ^∞ ((x^4 −2x^2 +2)/(x(√(x^2 −1))))dx=∫_1 ^∞ {(((x^2 −1)^2 )/(x(√(x^2 −1))))+(1/(x(√(x^2 −1))))}dx =∫_1 ^∞ {(((x^2 −1)^(3/2) )/x)+(((x^2 −1)^(−(1/2)) )/x)}dx x^2 =u ⇒2xdx=du =(1/2)∫_1 ^∞ {(((u−1)^(3/2) )/u)+(((u−1)^(−(1/2)) )/u)}du (1/u)=v ⇒−(du/u^2 )=dv ⇒du=−(dv/v^2 ) ∅=(1/2)∫_0 ^1 {v((1/v)−1)^(3/2) +v((1/v)−1)^(−(1/2)) }(dv/v^2 ) =(1/2)∫_0 ^1 {v^(−(5/2)) (1−v)^(3/2) +v^(−(1/2)) (1−v)^(−(1/2)) }dv =(1/2){β(−(3/2),(5/2))+β((1/2),(1/2))} But for β(m,n), n,m>0... Maybe some error occured. Please check.

$$\emptyset=\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{x}^{\mathrm{4}} −\mathrm{2x}^{\mathrm{2}} +\mathrm{2}}{\mathrm{x}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}\mathrm{dx}=\int_{\mathrm{1}} ^{\infty} \left\{\frac{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{x}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}+\frac{\mathrm{1}}{\mathrm{x}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}\right\}\mathrm{dx} \\ $$$$\:\:\:=\int_{\mathrm{1}} ^{\infty} \left\{\frac{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{x}}+\frac{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{x}}\right\}\mathrm{dx} \\ $$$$\mathrm{x}^{\mathrm{2}} =\mathrm{u}\:\Rightarrow\mathrm{2xdx}=\mathrm{du}\: \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\infty} \left\{\frac{\left(\mathrm{u}−\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{u}}+\frac{\left(\mathrm{u}−\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{u}}\right\}\mathrm{du} \\ $$$$\frac{\mathrm{1}}{\mathrm{u}}=\mathrm{v}\:\Rightarrow−\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} }=\mathrm{dv}\:\Rightarrow\mathrm{du}=−\frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} } \\ $$$$\emptyset=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\mathrm{v}\left(\frac{\mathrm{1}}{\mathrm{v}}−\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\mathrm{v}\left(\frac{\mathrm{1}}{\mathrm{v}}−\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right\}\frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} } \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\mathrm{v}^{−\frac{\mathrm{5}}{\mathrm{2}}} \left(\mathrm{1}−\mathrm{v}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\mathrm{v}^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−\mathrm{v}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right\}\mathrm{dv} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\beta\left(−\frac{\mathrm{3}}{\mathrm{2}},\frac{\mathrm{5}}{\mathrm{2}}\right)+\beta\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)\right\} \\ $$$$ \\ $$$$\mathrm{But}\:\mathrm{for}\:\beta\left(\mathrm{m},\mathrm{n}\right),\:\mathrm{n},\mathrm{m}>\mathrm{0}... \\ $$$$\mathrm{Maybe}\:\mathrm{some}\:\mathrm{error}\:\mathrm{occured}.\:\mathrm{Please}\:\mathrm{check}. \\ $$

Commented by Ar Brandon last updated on 03/Jan/21

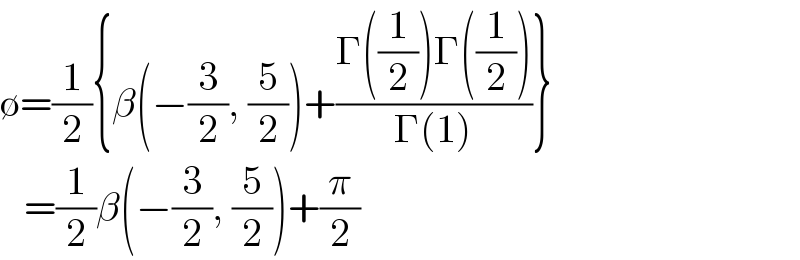
∅=(1/2){β(−(3/2), (5/2))+((Γ((1/2))Γ((1/2)))/(Γ(1)))} =(1/2)β(−(3/2), (5/2))+(π/2)

$$\emptyset=\frac{\mathrm{1}}{\mathrm{2}}\left\{\beta\left(−\frac{\mathrm{3}}{\mathrm{2}},\:\frac{\mathrm{5}}{\mathrm{2}}\right)+\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{1}\right)}\right\} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\beta\left(−\frac{\mathrm{3}}{\mathrm{2}},\:\frac{\mathrm{5}}{\mathrm{2}}\right)+\frac{\pi}{\mathrm{2}} \\ $$

Commented by mnjuly1970 last updated on 03/Jan/21

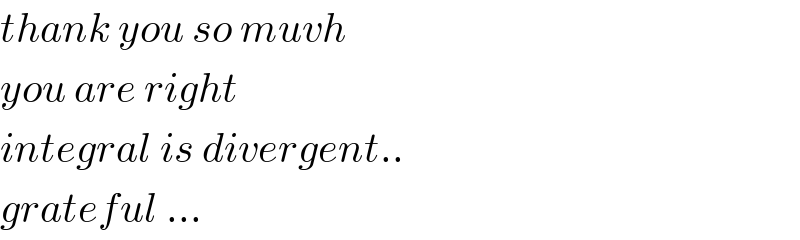
thank you so muvh you are right integral is divergent.. grateful ...

$${thank}\:{you}\:{so}\:{muvh}\: \\ $$$${you}\:{are}\:{right} \\ $$$${integral}\:{is}\:{divergent}.. \\ $$$${grateful}\:... \\ $$

Commented by Ar Brandon last updated on 03/Jan/21

My pleasure, Sir

$$\mathrm{My}\:\mathrm{pleasure},\:\mathrm{Sir} \\ $$

Answered by Dwaipayan Shikari last updated on 03/Jan/21

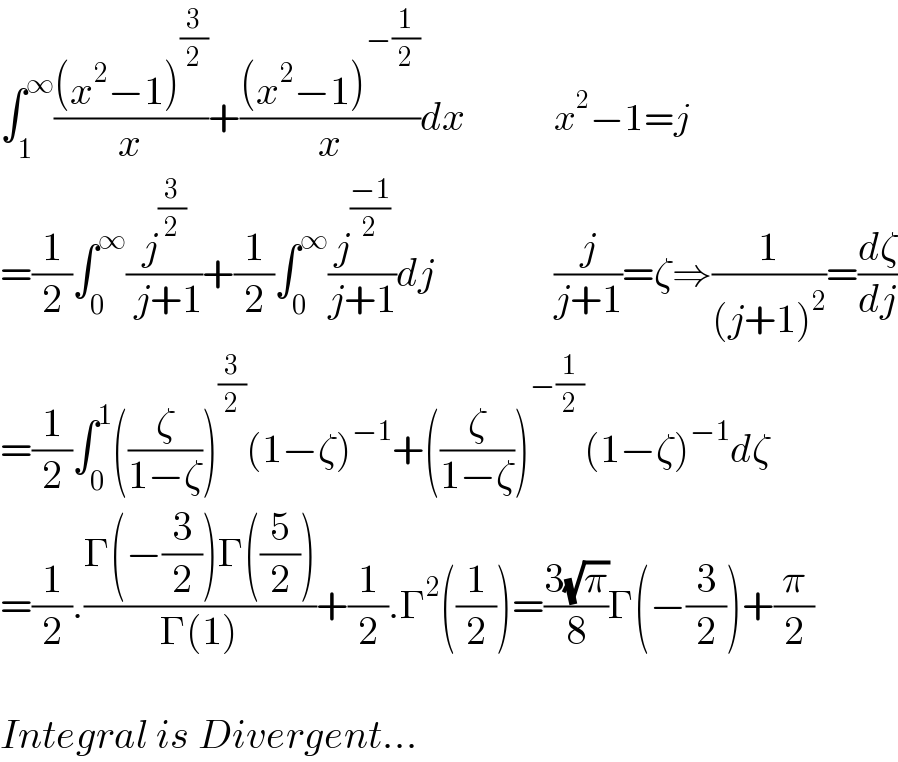
∫_1 ^∞ (((x^2 −1)^(3/2) )/x)+(((x^2 −1)^(−(1/2)) )/x)dx x^2 −1=j =(1/2)∫_0 ^∞ (j^(3/2) /( j+1))+(1/2)∫_0 ^∞ (j^((−1)/2) /(j+1))dj (j/(j+1))=ζ⇒(1/((j+1)^2 ))=(dζ/dj) =(1/2)∫_0 ^1 ((ζ/(1−ζ)))^(3/2) (1−ζ)^(−1) +((ζ/(1−ζ)))^(−(1/2)) (1−ζ)^(−1) dζ =(1/2).((Γ(−(3/2))Γ((5/2)))/(Γ(1)))+(1/2).Γ^2 ((1/2))=((3(√π))/8)Γ(−(3/2))+(π/2) Integral is Divergent...

$$\int_{\mathrm{1}} ^{\infty} \frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{{x}}+\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} }{{x}}{dx}\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} −\mathrm{1}={j} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{j}^{\frac{\mathrm{3}}{\mathrm{2}}} }{\:{j}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{j}^{\frac{−\mathrm{1}}{\mathrm{2}}} }{{j}+\mathrm{1}}{dj}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{j}}{{j}+\mathrm{1}}=\zeta\Rightarrow\frac{\mathrm{1}}{\left({j}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{{d}\zeta}{{dj}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\zeta}{\mathrm{1}−\zeta}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{1}−\zeta\right)^{−\mathrm{1}} +\left(\frac{\zeta}{\mathrm{1}−\zeta}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−\zeta\right)^{−\mathrm{1}} {d}\zeta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\Gamma\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}}.\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{3}\sqrt{\pi}}{\mathrm{8}}\Gamma\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)+\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$$${Integral}\:{is}\:{Divergent}... \\ $$

Commented by Ar Brandon last updated on 03/Jan/21

cool bro 😃

$$\mathrm{cool}\:\mathrm{bro} \\ $$😃

Commented by Dwaipayan Shikari last updated on 03/Jan/21

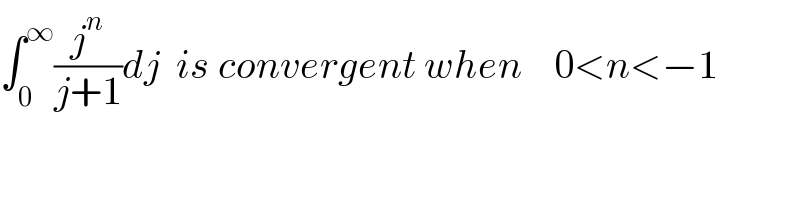
∫_0 ^∞ (j^n /(j+1))dj is convergent when 0<n<−1

$$\int_{\mathrm{0}} ^{\infty} \frac{{j}^{{n}} }{{j}+\mathrm{1}}{dj}\:\:{is}\:{convergent}\:{when}\:\:\:\:\mathrm{0}<{n}<−\mathrm{1} \\ $$

Commented by Dwaipayan Shikari last updated on 03/Jan/21

🍎

$$ \\ $$🍎

Terms of Service

Privacy Policy

Contact: info@tinkutara.com