
Question Number 197191 by tri26112004 last updated on 10/Sep/23
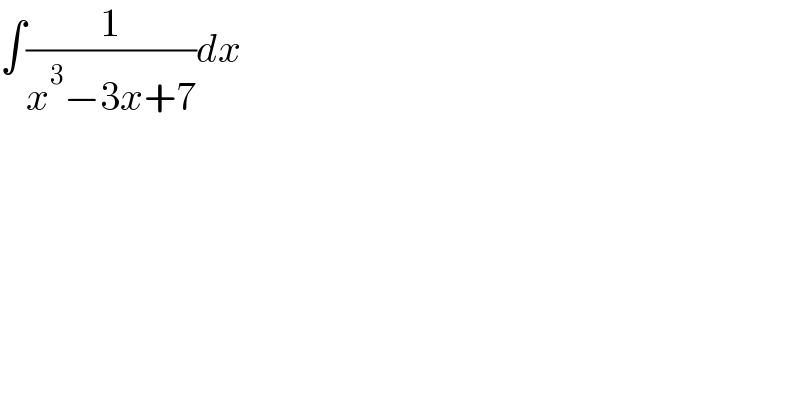
$$\int\frac{\mathrm{1}}{{x}^{\mathrm{3}} −\mathrm{3}{x}+\mathrm{7}}{dx} \\ $$
Answered by Frix last updated on 10/Sep/23
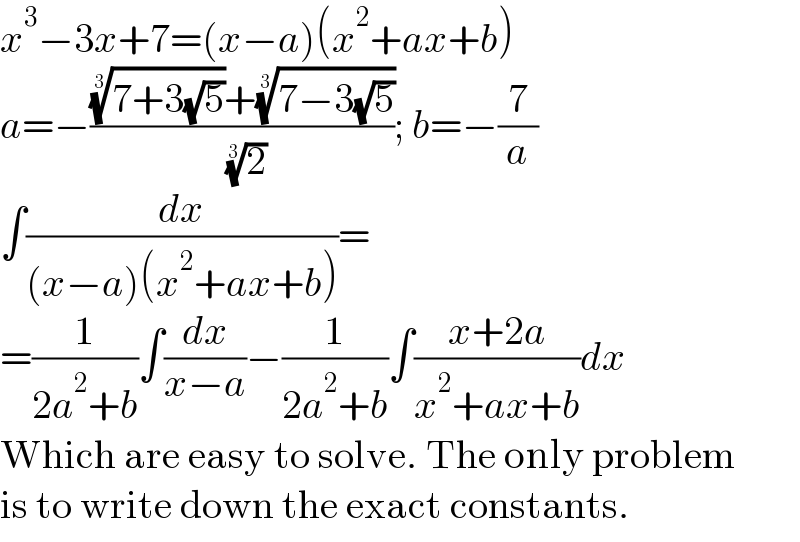
$${x}^{\mathrm{3}} −\mathrm{3}{x}+\mathrm{7}=\left({x}−{a}\right)\left({x}^{\mathrm{2}} +{ax}+{b}\right) \\ $$$${a}=−\frac{\sqrt[{\mathrm{3}}]{\mathrm{7}+\mathrm{3}\sqrt{\mathrm{5}}}+\sqrt[{\mathrm{3}}]{\mathrm{7}−\mathrm{3}\sqrt{\mathrm{5}}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}};\:{b}=−\frac{\mathrm{7}}{{a}} \\ $$$$\int\frac{{dx}}{\left({x}−{a}\right)\left({x}^{\mathrm{2}} +{ax}+{b}\right)}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} +{b}}\int\frac{{dx}}{{x}−{a}}−\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} +{b}}\int\frac{{x}+\mathrm{2}{a}}{{x}^{\mathrm{2}} +{ax}+{b}}{dx} \\ $$$$\mathrm{Which}\:\mathrm{are}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve}.\:\mathrm{The}\:\mathrm{only}\:\mathrm{problem} \\ $$$$\mathrm{is}\:\mathrm{to}\:\mathrm{write}\:\mathrm{down}\:\mathrm{the}\:\mathrm{exact}\:\mathrm{constants}. \\ $$
