
Question Number 136313 by aurpeyz last updated on 20/Mar/21
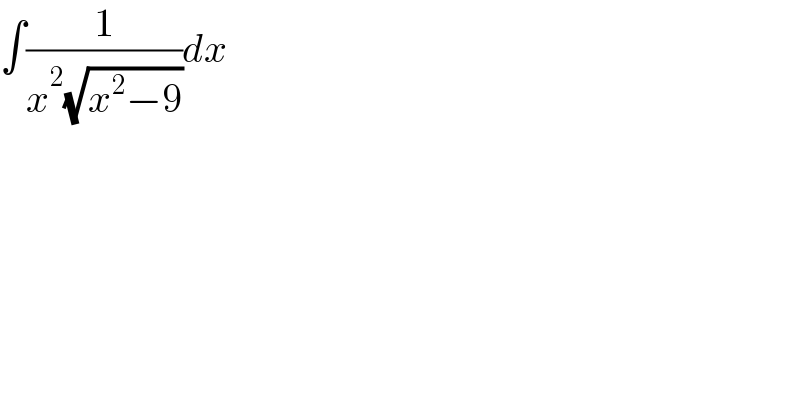
$$\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} −\mathrm{9}}}{dx} \\ $$
Answered by liberty last updated on 20/Mar/21
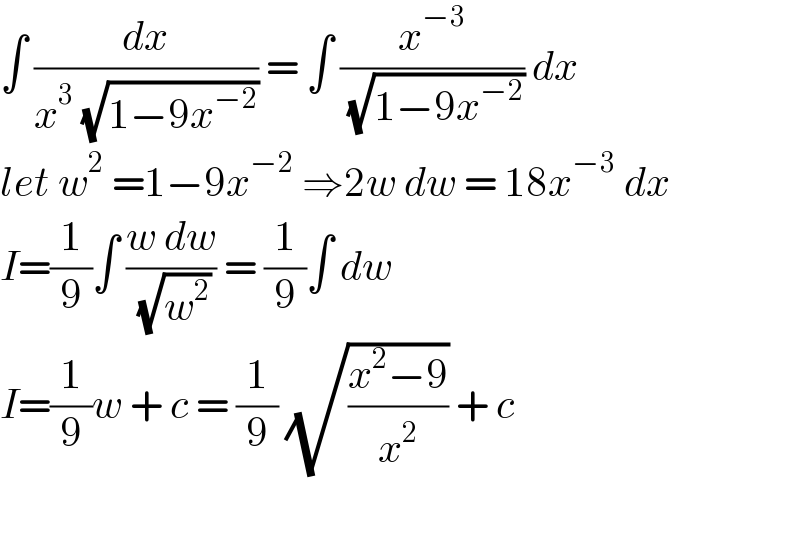
$$\int\:\frac{{dx}}{{x}^{\mathrm{3}} \:\sqrt{\mathrm{1}−\mathrm{9}{x}^{−\mathrm{2}} }}\:=\:\int\:\frac{{x}^{−\mathrm{3}} }{\:\sqrt{\mathrm{1}−\mathrm{9}{x}^{−\mathrm{2}} }}\:{dx}\: \\ $$$${let}\:{w}^{\mathrm{2}} \:=\mathrm{1}−\mathrm{9}{x}^{−\mathrm{2}} \:\Rightarrow\mathrm{2}{w}\:{dw}\:=\:\mathrm{18}{x}^{−\mathrm{3}} \:{dx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{9}}\int\:\frac{{w}\:{dw}}{\:\sqrt{{w}^{\mathrm{2}} }}\:=\:\frac{\mathrm{1}}{\mathrm{9}}\int\:{dw}\: \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{9}}{w}\:+\:{c}\:=\:\frac{\mathrm{1}}{\mathrm{9}}\:\sqrt{\frac{{x}^{\mathrm{2}} −\mathrm{9}}{{x}^{\mathrm{2}} }}\:+\:{c} \\ $$$$ \\ $$
Answered by Olaf last updated on 20/Mar/21

$$\mathrm{F}\left({x}\right)\:=\:\int\frac{{dx}}{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} −\mathrm{9}}} \\ $$$$\mathrm{Let}\:{x}\:=\:\mathrm{3ch}{u} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\int\frac{\mathrm{3sh}{u}}{\mathrm{9ch}^{\mathrm{2}} {u}\sqrt{\mathrm{9ch}^{\mathrm{2}} {u}−\mathrm{9}}}\:{du} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{sh}{u}}{\mathrm{ch}^{\mathrm{2}} {u}×\mathrm{3sh}{u}}\:{du} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{9}}\int\frac{{du}}{\mathrm{ch}^{\mathrm{2}} {u}}\: \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{9}}\int\left(\mathrm{1}−\mathrm{th}^{\mathrm{2}} {u}\right){du} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{9}}\mathrm{th}{u}+\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{9}}\mathrm{th}\left(\mathrm{argch}\frac{{x}}{\mathrm{3}}\right)+\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{9}}.\frac{{e}^{\mathrm{argch}\frac{{x}}{\mathrm{3}}} −{e}^{−\mathrm{argch}\frac{{x}}{\mathrm{3}}} }{{e}^{\mathrm{argch}\frac{{x}}{\mathrm{3}}} +{e}^{−\mathrm{argch}\frac{{x}}{\mathrm{3}}} }+\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{9}}.\frac{{e}^{\mathrm{ln}\left(\frac{{x}}{\mathrm{3}}+\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{9}}−\mathrm{1}}\right)} −{e}^{−\mathrm{ln}\left(\frac{{x}}{\mathrm{3}}+\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{9}}−\mathrm{1}}\right)} }{{e}^{\mathrm{ln}\left(\frac{{x}}{\mathrm{3}}+\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{9}}−\mathrm{1}}\right)} +{e}^{−\mathrm{ln}\left(\frac{{x}}{\mathrm{3}}+\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{9}}−\mathrm{1}}\right)} }+\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{9}}.\frac{\frac{{x}}{\mathrm{3}}+\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{9}}−\mathrm{1}}−\frac{\mathrm{1}}{\frac{{x}}{\mathrm{3}}+\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{9}}−\mathrm{1}}}}{\frac{{x}}{\mathrm{3}}+\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{9}}−\mathrm{1}}+\frac{\mathrm{1}}{\frac{{x}}{\mathrm{3}}+\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{9}}−\mathrm{1}}}}+\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{9}}.\frac{\frac{{x}}{\mathrm{3}}+\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{9}}−\mathrm{1}}−\left(\frac{{x}}{\mathrm{3}}−\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{9}}−\mathrm{1}}\right)}{\frac{{x}}{\mathrm{3}}+\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{9}}−\mathrm{1}}+\left(\frac{{x}}{\mathrm{3}}−\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{9}}−\mathrm{1}}\right)}+\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{9}}.\frac{\mathrm{2}\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{9}}−\mathrm{1}}}{\frac{\mathrm{2}{x}}{\mathrm{3}}}+\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}}.\frac{\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{9}}−\mathrm{1}}}{{x}}+\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{9}{x}}\sqrt{{x}^{\mathrm{2}} −\mathrm{9}}+\mathrm{C} \\ $$
Answered by mathmax by abdo last updated on 20/Mar/21
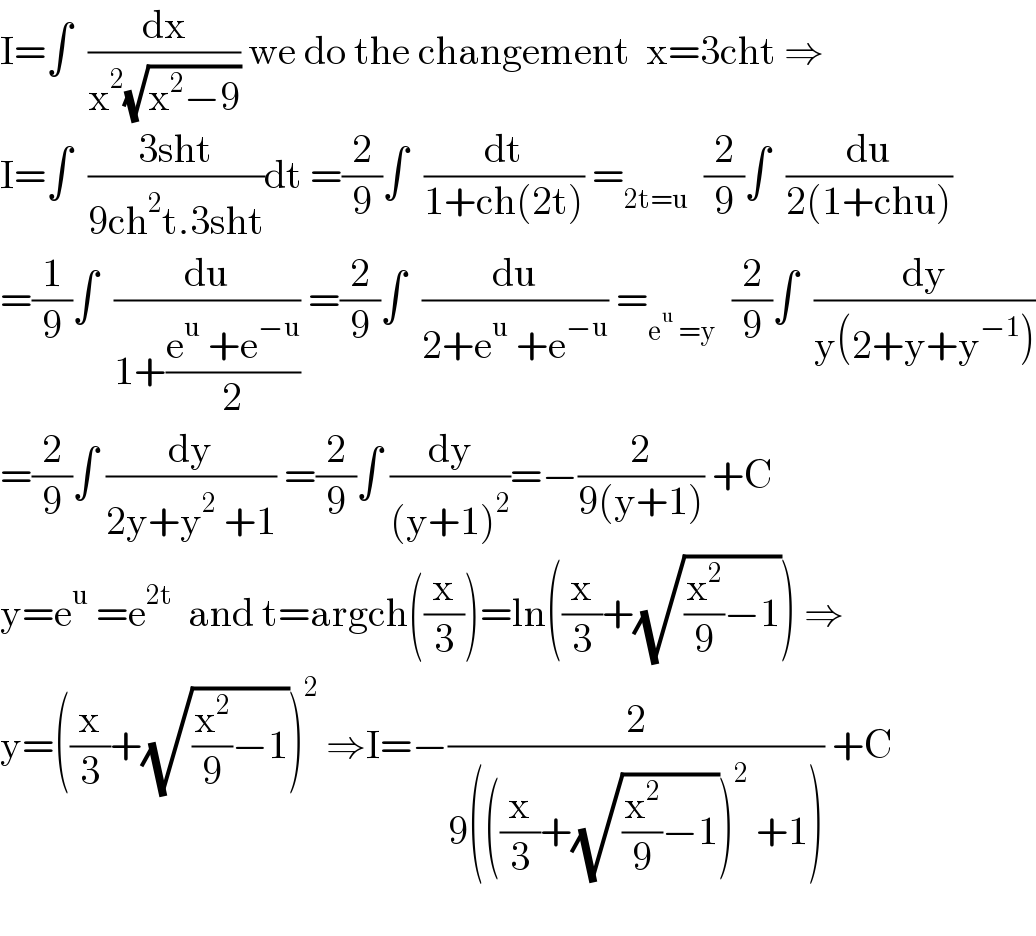
$$\mathrm{I}=\int\:\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{9}}}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\:\mathrm{x}=\mathrm{3cht}\:\Rightarrow \\ $$$$\mathrm{I}=\int\:\:\frac{\mathrm{3sht}}{\mathrm{9ch}^{\mathrm{2}} \mathrm{t}.\mathrm{3sht}}\mathrm{dt}\:=\frac{\mathrm{2}}{\mathrm{9}}\int\:\:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{ch}\left(\mathrm{2t}\right)}\:=_{\mathrm{2t}=\mathrm{u}} \:\:\frac{\mathrm{2}}{\mathrm{9}}\int\:\:\frac{\mathrm{du}}{\mathrm{2}\left(\mathrm{1}+\mathrm{chu}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\int\:\:\frac{\mathrm{du}}{\mathrm{1}+\frac{\mathrm{e}^{\mathrm{u}} \:+\mathrm{e}^{−\mathrm{u}} }{\mathrm{2}}}\:=\frac{\mathrm{2}}{\mathrm{9}}\int\:\:\frac{\mathrm{du}}{\mathrm{2}+\mathrm{e}^{\mathrm{u}} \:+\mathrm{e}^{−\mathrm{u}} }\:=_{\mathrm{e}^{\mathrm{u}} \:=\mathrm{y}} \:\:\frac{\mathrm{2}}{\mathrm{9}}\int\:\:\frac{\mathrm{dy}}{\mathrm{y}\left(\mathrm{2}+\mathrm{y}+\mathrm{y}^{−\mathrm{1}} \right)} \\ $$$$=\frac{\mathrm{2}}{\mathrm{9}}\int\:\frac{\mathrm{dy}}{\mathrm{2y}+\mathrm{y}^{\mathrm{2}} \:+\mathrm{1}}\:=\frac{\mathrm{2}}{\mathrm{9}}\int\:\frac{\mathrm{dy}}{\left(\mathrm{y}+\mathrm{1}\right)^{\mathrm{2}} }=−\frac{\mathrm{2}}{\mathrm{9}\left(\mathrm{y}+\mathrm{1}\right)}\:+\mathrm{C} \\ $$$$\mathrm{y}=\mathrm{e}^{\mathrm{u}} \:=\mathrm{e}^{\mathrm{2t}} \:\:\mathrm{and}\:\mathrm{t}=\mathrm{argch}\left(\frac{\mathrm{x}}{\mathrm{3}}\right)=\mathrm{ln}\left(\frac{\mathrm{x}}{\mathrm{3}}+\sqrt{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{9}}−\mathrm{1}}\right)\:\Rightarrow \\ $$$$\mathrm{y}=\left(\frac{\mathrm{x}}{\mathrm{3}}+\sqrt{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{9}}−\mathrm{1}}\right)^{\mathrm{2}} \:\Rightarrow\mathrm{I}=−\frac{\mathrm{2}}{\mathrm{9}\left(\left(\frac{\mathrm{x}}{\mathrm{3}}+\sqrt{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{9}}−\mathrm{1}}\right)^{\mathrm{2}} \:+\mathrm{1}\right)}\:+\mathrm{C} \\ $$$$ \\ $$
