
Question Number 144760 by mathdanisur last updated on 28/Jun/21
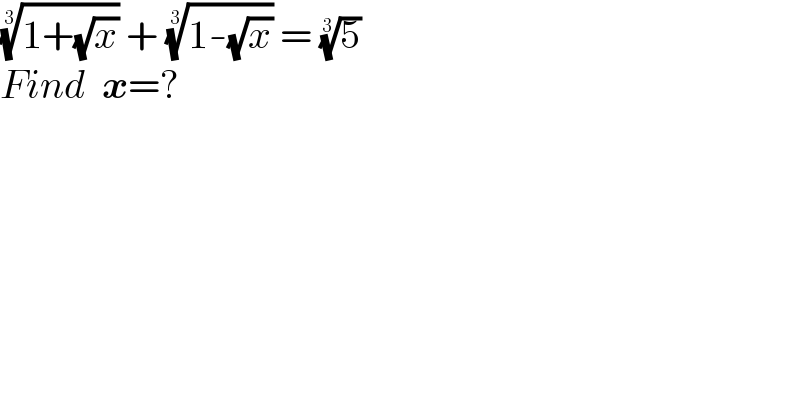
$$\sqrt[{\mathrm{3}}]{\mathrm{1}+\sqrt{{x}}}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{1}-\sqrt{{x}}}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{5}} \\ $$$${Find}\:\:\boldsymbol{{x}}=? \\ $$
Answered by Olaf_Thorendsen last updated on 28/Jun/21
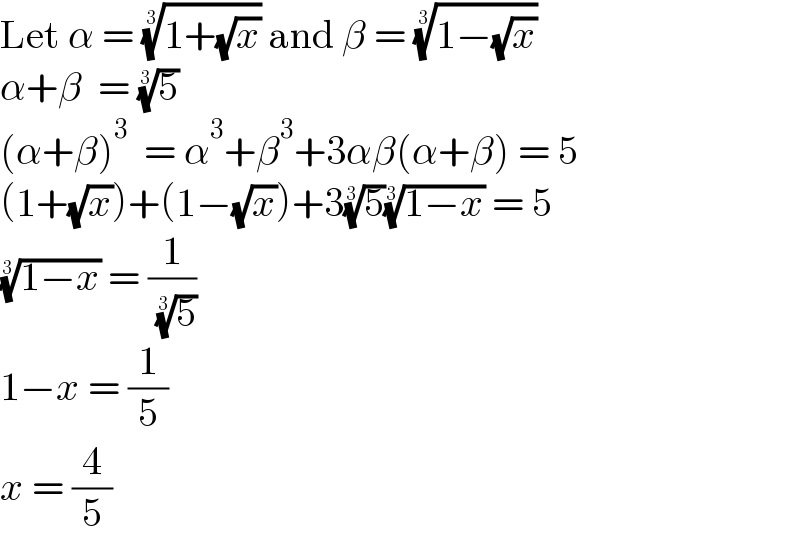
$$\mathrm{Let}\:\alpha\:=\:\sqrt[{\mathrm{3}}]{\mathrm{1}+\sqrt{{x}}}\:\mathrm{and}\:\beta\:=\:\sqrt[{\mathrm{3}}]{\mathrm{1}−\sqrt{{x}}} \\ $$$$\alpha+\beta\:\:=\:\sqrt[{\mathrm{3}}]{\mathrm{5}} \\ $$$$\left(\alpha+\beta\right)^{\mathrm{3}} \:\:=\:\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} +\mathrm{3}\alpha\beta\left(\alpha+\beta\right)\:=\:\mathrm{5} \\ $$$$\left(\mathrm{1}+\sqrt{{x}}\right)+\left(\mathrm{1}−\sqrt{{x}}\right)+\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{5}}\sqrt[{\mathrm{3}}]{\mathrm{1}−{x}}\:=\:\mathrm{5} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{1}−{x}}\:=\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{5}}} \\ $$$$\mathrm{1}−{x}\:=\:\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${x}\:=\:\frac{\mathrm{4}}{\mathrm{5}} \\ $$
Commented by mathdanisur last updated on 29/Jun/21
$${cool}\:{Sir}\:{thankyou} \\ $$
