
Question Number 4943 by madscientist last updated on 25/Mar/16
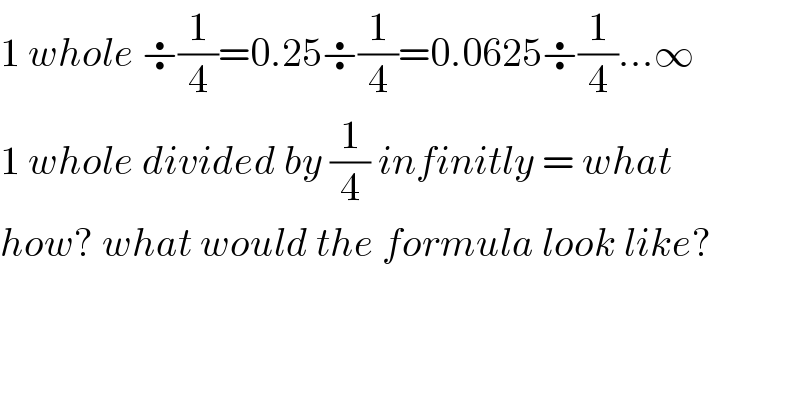
$$\mathrm{1}\:{whole}\:\boldsymbol{\div}\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0}.\mathrm{25}\boldsymbol{\div}\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0}.\mathrm{0625}\boldsymbol{\div}\frac{\mathrm{1}}{\mathrm{4}}...\infty \\ $$$$\mathrm{1}\:{whole}\:{divided}\:{by}\:\frac{\mathrm{1}}{\mathrm{4}}\:{infinitly}\:=\:{what} \\ $$$${how}?\:{what}\:{would}\:{the}\:{formula}\:{look}\:{like}? \\ $$
Commented by FilupSmith last updated on 25/Mar/16
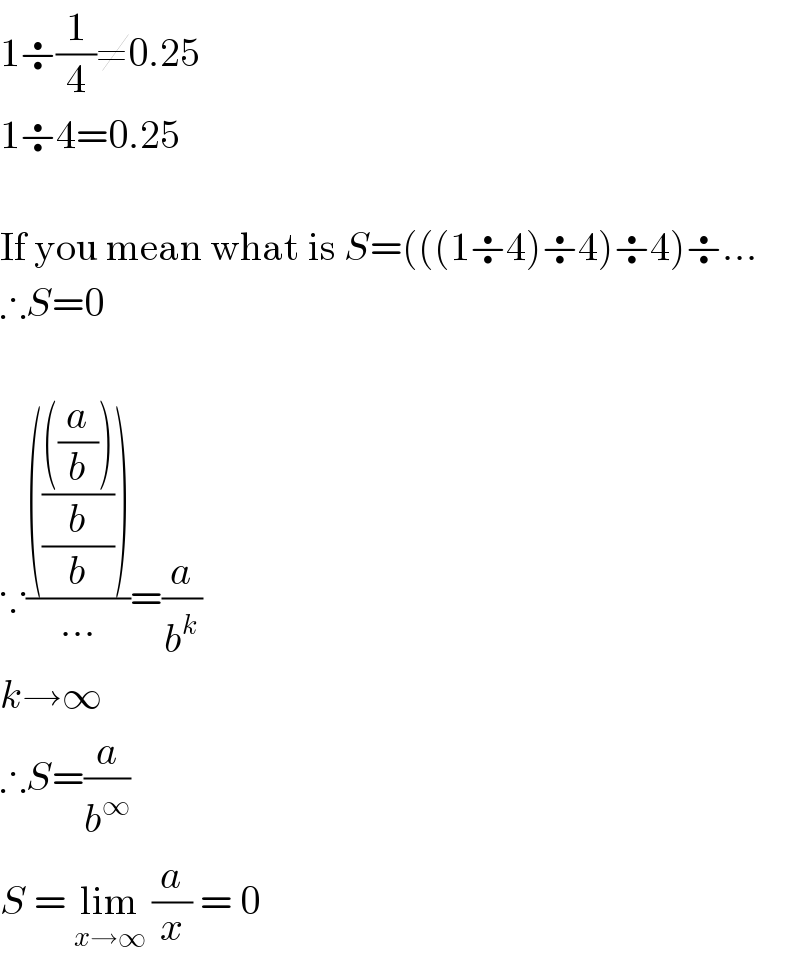
$$\mathrm{1}\boldsymbol{\div}\frac{\mathrm{1}}{\mathrm{4}}\neq\mathrm{0}.\mathrm{25} \\ $$$$\mathrm{1}\boldsymbol{\div}\mathrm{4}=\mathrm{0}.\mathrm{25} \\ $$$$ \\ $$$$\mathrm{If}\:\mathrm{you}\:\mathrm{mean}\:\mathrm{what}\:\mathrm{is}\:{S}=\left(\left(\left(\mathrm{1}\boldsymbol{\div}\mathrm{4}\right)\boldsymbol{\div}\mathrm{4}\right)\boldsymbol{\div}\mathrm{4}\right)\boldsymbol{\div}... \\ $$$$\therefore{S}=\mathrm{0} \\ $$$$ \\ $$$$\because\frac{\left(\frac{\frac{\left(\frac{{a}}{{b}}\right)}{{b}}}{{b}}\right)}{...}=\frac{{a}}{{b}^{{k}} } \\ $$$${k}\rightarrow\infty \\ $$$$\therefore{S}=\frac{{a}}{{b}^{\infty} } \\ $$$${S}\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{a}}{{x}}\:=\:\mathrm{0} \\ $$
Answered by FilupSmith last updated on 25/Mar/16

$$\frac{{a}}{\left(\frac{{b}}{{c}}\right)}=\frac{{ac}}{{b}} \\ $$$$\:\mathrm{1}\boldsymbol{\div}\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{4} \\ $$$$\mathrm{4}\boldsymbol{\div}\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{16} \\ $$$$\mathrm{16}\boldsymbol{\div}\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{64} \\ $$$$... \\ $$$$ \\ $$$$\therefore\:\mathrm{it}\:\mathrm{diverges}\:\mathrm{towards}\:\infty \\ $$
