
Question Number 163082 by HongKing last updated on 03/Jan/22
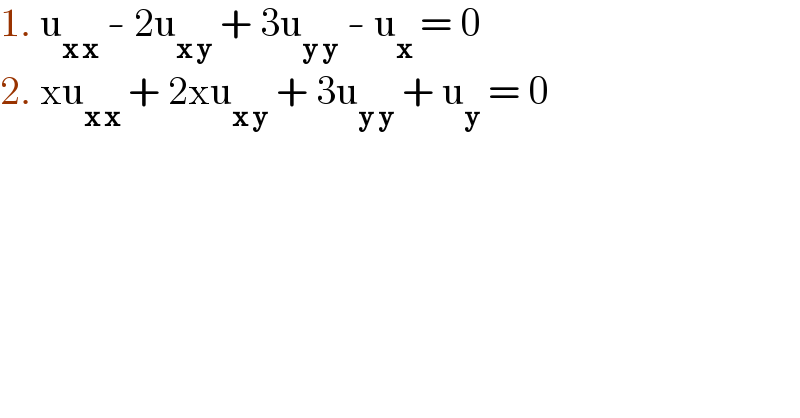
$$\mathrm{1}.\:\mathrm{u}_{\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{x}}} \:-\:\mathrm{2u}_{\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{y}}} \:+\:\mathrm{3u}_{\boldsymbol{\mathrm{y}}\:\boldsymbol{\mathrm{y}}} \:-\:\mathrm{u}_{\boldsymbol{\mathrm{x}}} \:=\:\mathrm{0} \\ $$$$\mathrm{2}.\:\mathrm{xu}_{\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{x}}} \:+\:\mathrm{2xu}_{\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{y}}} \:+\:\mathrm{3u}_{\boldsymbol{\mathrm{y}}\:\boldsymbol{\mathrm{y}}} \:+\:\mathrm{u}_{\boldsymbol{\mathrm{y}}} \:=\:\mathrm{0} \\ $$
Commented by mahdipoor last updated on 03/Jan/22
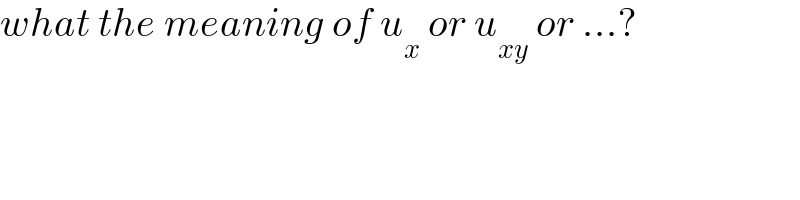
$${what}\:{the}\:{meaning}\:{of}\:{u}_{{x}} \:{or}\:{u}_{{xy}} \:{or}\:...? \\ $$
Commented by mr W last updated on 03/Jan/22

$${u}_{{x}} =\frac{\partial{u}}{\partial{x}} \\ $$$${u}_{{y}} =\frac{\partial{u}}{\partial{y}} \\ $$$${u}_{{xx}} =\frac{\partial^{\mathrm{2}} {u}}{\partial{x}^{\mathrm{2}} } \\ $$$${u}_{{xy}} =\frac{\partial^{\mathrm{2}} {u}}{\partial{x}\partial{y}} \\ $$$$... \\ $$
Commented by mahdipoor last updated on 03/Jan/22

$${thank}\:{ser}\:{W}\: \\ $$
