
Question Number 153574 by otchereabdullai@gmail.com last updated on 08/Sep/21

$$\left.\:\mathrm{1}\right)\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{a}\:\mathrm{spherical}\:\mathrm{ballon}\:\mathrm{is}\: \\ $$$$\mathrm{increasing}\:\mathrm{at}\:\mathrm{the}\:\mathrm{rate}\:\mathrm{of}\:\mathrm{3cms}^{−\mathrm{1}} \:.\:\mathrm{find} \\ $$$$\mathrm{the}\:\mathrm{rate}\:\mathrm{in}\:\mathrm{the}\:\mathrm{surface}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{ballon} \\ $$$$\mathrm{when}\:\mathrm{its}\:\mathrm{radius}\:\mathrm{is}\:\mathrm{10cm} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:\mathrm{evaluate}\:\int\frac{\mathrm{5}}{\left(\mathrm{3x}−\mathrm{2}\right)^{\mathrm{4}} }\mathrm{dx} \\ $$
Answered by TheSupreme last updated on 08/Sep/21
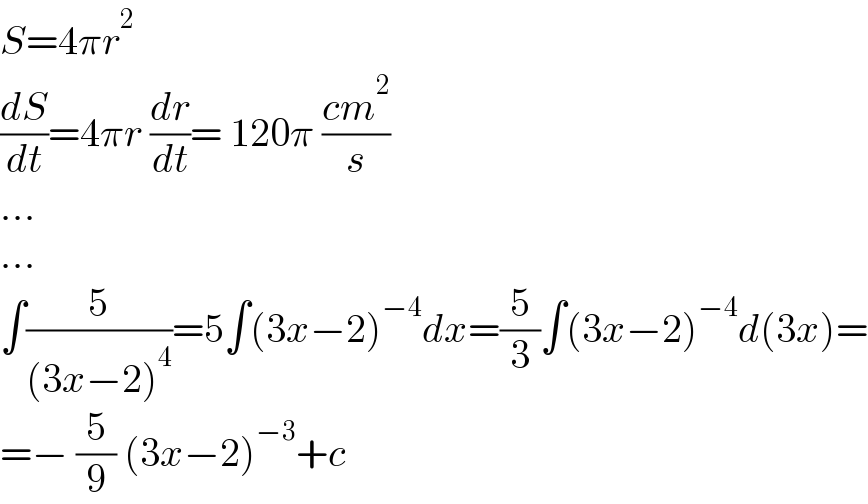
$${S}=\mathrm{4}\pi{r}^{\mathrm{2}} \\ $$$$\frac{{dS}}{{dt}}=\mathrm{4}\pi{r}\:\frac{{dr}}{{dt}}=\:\mathrm{120}\pi\:\frac{{cm}^{\mathrm{2}} }{{s}} \\ $$$$... \\ $$$$... \\ $$$$\int\frac{\mathrm{5}}{\left(\mathrm{3}{x}−\mathrm{2}\right)^{\mathrm{4}} }=\mathrm{5}\int\left(\mathrm{3}{x}−\mathrm{2}\right)^{−\mathrm{4}} {dx}=\frac{\mathrm{5}}{\mathrm{3}}\int\left(\mathrm{3}{x}−\mathrm{2}\right)^{−\mathrm{4}} {d}\left(\mathrm{3}{x}\right)= \\ $$$$=−\:\frac{\mathrm{5}}{\mathrm{9}}\:\left(\mathrm{3}{x}−\mathrm{2}\right)^{−\mathrm{3}} +{c} \\ $$
