
Question Number 122976 by bemath last updated on 21/Nov/20
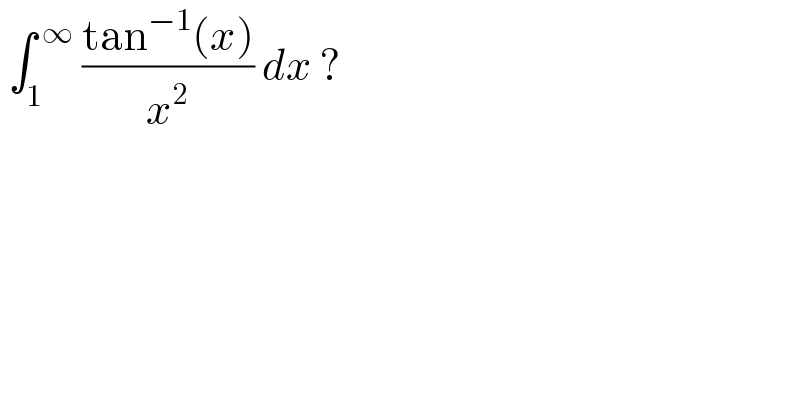
$$\:\int_{\mathrm{1}} ^{\:\infty} \:\frac{\mathrm{tan}^{−\mathrm{1}} \left({x}\right)}{{x}^{\mathrm{2}} }\:{dx}\:? \\ $$
Answered by mnjuly1970 last updated on 21/Nov/20
![solution:: (1/x)=t⇒((−dx)/x^2 )=dt ∫_0 ^( 1) tan^(−1) ((1/t))dt=(π/2)−∫_0 ^( 1) tan^(−1) (t)dt (π/2)−[t(tan^(−1) (t))]_0 ^1 +∫_0 ^( 1) (t/(1+t^2 ))dt =(π/2)−(π/4)+(1/2)ln(2)=(π/4)+(1/2)ln(2)✓](Q123016.png)
$${solution}:: \\ $$$$\:\:\frac{\mathrm{1}}{{x}}={t}\Rightarrow\frac{−{dx}}{{x}^{\mathrm{2}} }={dt} \\ $$$$\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{t}}\right){dt}=\frac{\pi}{\mathrm{2}}−\int_{\mathrm{0}} ^{\:\mathrm{1}} {tan}^{−\mathrm{1}} \left({t}\right){dt} \\ $$$$\:\:\:\:\:\frac{\pi}{\mathrm{2}}−\left[{t}\left({tan}^{−\mathrm{1}} \left({t}\right)\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right)=\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\checkmark \\ $$
Answered by TANMAY PANACEA last updated on 21/Nov/20
![x=tana→dx=sec^2 ada ∫_(π/4) ^(π/2) ((a×sec^2 a)/(tan^2 a)) a∫((d(tana))/(tan^2 a))−∫[(da/da)∫((d(tana))/(tan^2 a))]da a×((−1)/(tana))+∫(da/(tana)) ((−a)/(tana))+ln(sina)+C ■∣((−a)/(tana))+lnsina∣^(π/2) _(π/4) −((π/2)/(tan(π/2)))+((π/4)/(tan(π/4)))+lnsin(π/2)−lnsin(π/4) =((−(π/2))/∞)+((π/4)/1)+ln1−ln((1/( (√2)))) (π/4)−ln((1/( (√2))))=(π/4)−(ln1−ln(√2) )=(π/4)+ln(√2)](Q122978.png)
$${x}={tana}\rightarrow{dx}={sec}^{\mathrm{2}} {ada} \\ $$$$\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} \frac{{a}×{sec}^{\mathrm{2}} {a}}{{tan}^{\mathrm{2}} {a}} \\ $$$${a}\int\frac{{d}\left({tana}\right)}{{tan}^{\mathrm{2}} {a}}−\int\left[\frac{{da}}{{da}}\int\frac{{d}\left({tana}\right)}{{tan}^{\mathrm{2}} {a}}\right]{da} \\ $$$${a}×\frac{−\mathrm{1}}{{tana}}+\int\frac{{da}}{{tana}} \\ $$$$\frac{−{a}}{{tana}}+{ln}\left({sina}\right)+{C} \\ $$$$\blacksquare\mid\frac{−{a}}{{tana}}+{lnsina}\underset{\frac{\pi}{\mathrm{4}}} {\mid}^{\frac{\pi}{\mathrm{2}}} \\ $$$$−\frac{\frac{\pi}{\mathrm{2}}}{{tan}\frac{\pi}{\mathrm{2}}}+\frac{\frac{\pi}{\mathrm{4}}}{{tan}\frac{\pi}{\mathrm{4}}}+{lnsin}\frac{\pi}{\mathrm{2}}−{lnsin}\frac{\pi}{\mathrm{4}} \\ $$$$=\frac{−\frac{\pi}{\mathrm{2}}}{\infty}+\frac{\frac{\pi}{\mathrm{4}}}{\mathrm{1}}+{ln}\mathrm{1}−{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$$\frac{\pi}{\mathrm{4}}−{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)=\frac{\pi}{\mathrm{4}}−\left({ln}\mathrm{1}−{ln}\sqrt{\mathrm{2}}\:\right)=\frac{\pi}{\mathrm{4}}+{ln}\sqrt{\mathrm{2}} \\ $$
Answered by benjo_mathlover last updated on 21/Nov/20
![∫_1 ^∞ ((tan^(−1) (x))/x^2 ) dx ? by parts { ((u=tan^(−1) (x)⇒du=(dx/(1+x^2 )))),((dv=x^(−2) dx ⇒v=−x^(−1) )) :} ν = [ −x tan^(−1) (x) ]_1 ^∞ +∫_1 ^∞ (dx/(x(1+x^2 ))) ν= 0−(−(π/4))+∫_0 ^∞ ((1/x)−(x/((1+x^2 ))))dx ν = (π/4)+[ ln (x)−(1/2)ln (1+x^2 )]_0 ^∞ ν = (π/4) +(1/2)[ln ((x^2 /(1+x^2 )))]_1 ^∞ ν = (π/4)+(1/2)(0−ln ((1/2))) ν = (π/4) + ln (√2) .](Q122990.png)
$$\:\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{tan}^{−\mathrm{1}} \left({x}\right)}{{x}^{\mathrm{2}} }\:{dx}\:? \\ $$$${by}\:{parts}\:\begin{cases}{{u}=\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\Rightarrow{du}=\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }}\\{{dv}={x}^{−\mathrm{2}} {dx}\:\Rightarrow{v}=−{x}^{−\mathrm{1}} }\end{cases} \\ $$$$\nu\:=\:\left[\:−{x}\:\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\:\right]_{\mathrm{1}} ^{\infty} +\underset{\mathrm{1}} {\overset{\infty} {\int}}\:\frac{{dx}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$$$\nu=\:\mathrm{0}−\left(−\frac{\pi}{\mathrm{4}}\right)+\underset{\mathrm{0}} {\overset{\infty} {\int}}\left(\frac{\mathrm{1}}{{x}}−\frac{{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\right){dx} \\ $$$$\nu\:=\:\frac{\pi}{\mathrm{4}}+\left[\:\mathrm{ln}\:\left({x}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\infty} \: \\ $$$$\nu\:=\:\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{ln}\:\left(\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\right)\right]_{\mathrm{1}} ^{\infty} \\ $$$$\nu\:=\:\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{0}−\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$\nu\:=\:\frac{\pi}{\mathrm{4}}\:+\:\mathrm{ln}\:\sqrt{\mathrm{2}}\:.\: \\ $$
Answered by mathmax by abdo last updated on 21/Nov/20
![A =∫_1 ^∞ ((arctanx)/x^2 )dx by parts we get A =[−((arctanx)/x)]_1 ^∞ +∫_1 ^∞ (1/x)(dx/(1+x^2 )) =(π/4)+∫_1 ^∞ ((1/x)−(x/(1+x^2 )))dx =(π/4)+[ln∣x∣−ln((√(1+x^2 )))]_1 ^∞ =(π/4)+[ln∣(x/( (√(1+x^2 ))))∣]_1 ^∞ =(π/4)−ln((1/( (√2)))) =(π/4)+ln((√2)) =(π/4)+((ln(2))/2)](Q122992.png)
$$\mathrm{A}\:=\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{arctanx}}{\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\mathrm{by}\:\mathrm{parts}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{A}\:=\left[−\frac{\mathrm{arctanx}}{\mathrm{x}}\right]_{\mathrm{1}} ^{\infty} +\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{\mathrm{x}}\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:=\frac{\pi}{\mathrm{4}}+\int_{\mathrm{1}} ^{\infty} \:\left(\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx} \\ $$$$=\frac{\pi}{\mathrm{4}}+\left[\mathrm{ln}\mid\mathrm{x}\mid−\mathrm{ln}\left(\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\right]_{\mathrm{1}} ^{\infty} \:=\frac{\pi}{\mathrm{4}}+\left[\mathrm{ln}\mid\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\mid\right]_{\mathrm{1}} ^{\infty} \:=\frac{\pi}{\mathrm{4}}−\mathrm{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$$=\frac{\pi}{\mathrm{4}}+\mathrm{ln}\left(\sqrt{\mathrm{2}}\right)\:=\frac{\pi}{\mathrm{4}}+\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$
