
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 118489 by bramlexs22 last updated on 18/Oct/20

$$\left(\mathrm{1}\right)\:{solve}\:{the}\:{equation}\:\frac{{x}−\mathrm{49}}{\mathrm{50}}\:+\:\frac{{x}−\mathrm{50}}{\mathrm{49}}\:=\:\frac{\mathrm{49}}{{x}−\mathrm{50}}\:+\:\frac{\mathrm{50}}{{x}−\mathrm{49}} \\ $$$$\left(\mathrm{2}\right)\:{How}\:{many}\:{numbers}\:{from}\:\mathrm{12}\:{to}\:\mathrm{12345}\: \\ $$$${inclusive}\:{have}\:{digits}\:{which}\:{are}\: \\ $$$${consecutive}\:{an}\:{in}\:{increasing}\:{order}, \\ $$$${reading}\:{from}\:{left}\:{to}\:{right}\:?\: \\ $$
Answered by benjo_mathlover last updated on 18/Oct/20

$$\:{Solve}\:{the}\:{equation}\:\frac{{x}−\mathrm{49}}{\mathrm{50}}\:+\:\frac{{x}−\mathrm{50}}{\mathrm{49}}\:=\:\frac{\mathrm{49}}{{x}−\mathrm{50}}\:+\:\frac{\mathrm{50}}{{x}−\mathrm{49}} \\ $$$${solution}\::\: \\ $$$$\left(\bullet\right)\:\frac{{x}−\mathrm{49}}{\mathrm{50}}\:+\:\frac{{x}−\mathrm{50}}{\mathrm{49}}\:=\:\frac{\mathrm{49}}{{x}−\mathrm{50}}\:+\:\frac{\mathrm{50}}{{x}−\mathrm{49}} \\ $$$${let}\:\frac{{x}−\mathrm{49}}{\mathrm{50}}\:=\:{t}\:\rightarrow{x}=\mathrm{50}{t}+\mathrm{49} \\ $$$$\Rightarrow\:{t}\:+\:\frac{\mathrm{50}{t}−\mathrm{1}}{\mathrm{49}}\:=\:\frac{\mathrm{1}}{{t}}\:+\:\frac{\mathrm{50}}{\mathrm{50}{t}}\: \\ $$$$\Rightarrow\:{t}\:+\:\frac{\mathrm{50}{t}}{\mathrm{49}}\:−\frac{\mathrm{1}}{\mathrm{49}}\:=\:\frac{\mathrm{2}}{{t}} \\ $$$$\Rightarrow\frac{\mathrm{99}{t}}{\mathrm{49}}\:−\:\frac{\mathrm{2}}{{t}}\:=\:\frac{\mathrm{1}}{\mathrm{49}}\:;\:\mathrm{99}{t}^{\mathrm{2}} \:−\mathrm{98}\:=\:{t}\:\: \\ $$$$\Rightarrow\:\mathrm{99}{t}^{\mathrm{2}} −{t}−\mathrm{98}\:=\:\mathrm{0}\:;\:\left(\mathrm{99}{t}\:+\mathrm{98}\right)\left({t}−\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$$\begin{cases}{{t}=\mathrm{1}\:\Rightarrow{x}\:=\:\mathrm{99}}\\{{t}=−\frac{\mathrm{98}}{\mathrm{99}}\:\Rightarrow{x}\:=\:\mathrm{50}\left(−\frac{\mathrm{98}}{\mathrm{99}}\right)+\mathrm{49}\:=\:−\frac{\mathrm{49}}{\mathrm{99}}}\end{cases} \\ $$$$ \\ $$
Answered by som(math1967) last updated on 18/Oct/20
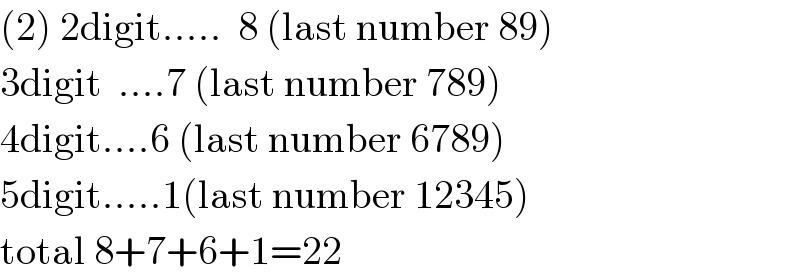
$$\left(\mathrm{2}\right)\:\mathrm{2digit}.....\:\:\mathrm{8}\:\left(\mathrm{last}\:\mathrm{number}\:\mathrm{89}\right) \\ $$$$\mathrm{3digit}\:\:....\mathrm{7}\:\left(\mathrm{last}\:\mathrm{number}\:\mathrm{789}\right) \\ $$$$\mathrm{4digit}....\mathrm{6}\:\left(\mathrm{last}\:\mathrm{number}\:\mathrm{6789}\right) \\ $$$$\mathrm{5digit}.....\mathrm{1}\left(\mathrm{last}\:\mathrm{number}\:\mathrm{12345}\right) \\ $$$$\mathrm{total}\:\mathrm{8}+\mathrm{7}+\mathrm{6}+\mathrm{1}=\mathrm{22}\: \\ $$
Commented by bramlexs22 last updated on 18/Oct/20

$${thank}\:{you}\:{sir} \\ $$
