
Question Number 153924 by ZiYangLee last updated on 12/Sep/21
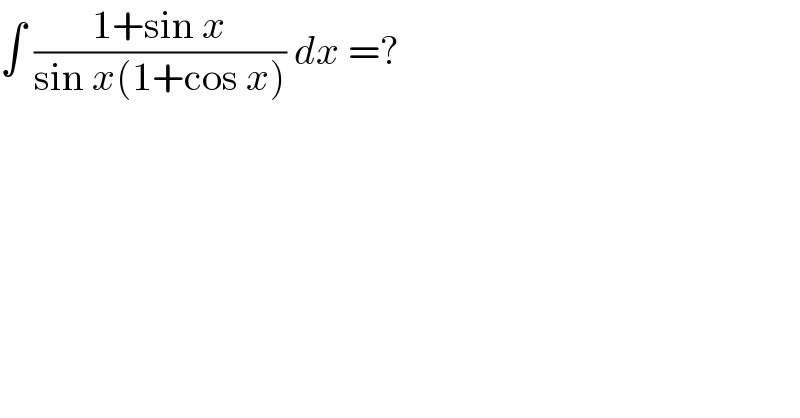
$$\int\:\frac{\mathrm{1}+\mathrm{sin}\:{x}}{\mathrm{sin}\:{x}\left(\mathrm{1}+\mathrm{cos}\:{x}\right)}\:{dx}\:=? \\ $$
Answered by ArielVyny last updated on 12/Sep/21

$$\int\frac{\left(\mathrm{1}+{sinx}\right)}{{sinx}\left(\mathrm{1}+{cosx}\right)}{dx}=\int\frac{\mathrm{1}}{{sinx}\left(\mathrm{1}+{cosx}\right)}+\int\frac{\mathrm{1}}{\mathrm{1}+{cosx}}{dx} \\ $$$${t}={tan}\left(\frac{{x}}{\mathrm{2}}\right)\rightarrow{dt}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dx} \\ $$$${dx}=\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\int\frac{\mathrm{1}}{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\left(\mathrm{1}+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)}×\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}+\int\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}.\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\int\frac{\mathrm{1}}{{t}\left(\mathrm{1}+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)}{dt}+\int\frac{\mathrm{1}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)+\mathrm{1}−{t}^{\mathrm{2}} }{dt} \\ $$$$\int\frac{\mathrm{1}}{{t}\left(\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)}{dt}+\int\frac{\mathrm{1}}{\mathrm{2}}{dt} \\ $$$$\int\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{2}{t}}{dt}+\frac{\mathrm{1}}{\mathrm{2}}{t}+{C} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{t}\mid+\frac{\mathrm{1}}{\mathrm{4}}{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{t}+{C} \\ $$$$\int\frac{\mathrm{1}+{sinx}}{{sinx}\left(\mathrm{1}+{cosx}\right)}{dt}={ln}\left(\sqrt{\mid{tan}\left(\frac{{x}}{\mathrm{2}}\right)\mid}\right)+\frac{\mathrm{1}}{\mathrm{4}}\left({tan}\left(\frac{{x}}{\mathrm{2}}\right)\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\left({tan}\left(\frac{{x}}{\mathrm{2}}\right)\right)+{C} \\ $$$$ \\ $$
Commented by Tawa11 last updated on 12/Sep/21

$$\mathrm{Weldone}\:\mathrm{sir}. \\ $$
Answered by puissant last updated on 12/Sep/21

$${Q}=\int\frac{\mathrm{1}+{sinx}}{{sinx}\left(\mathrm{1}+{cosx}\right)}{dx} \\ $$$${u}={tan}\left(\frac{{x}}{\mathrm{2}}\right)\rightarrow{x}=\mathrm{2}{arctan}\left({u}\right)\rightarrow{dx}=\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$${Q}=\int\frac{\mathrm{1}+\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}{\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }\left(\mathrm{1}+\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }\right)}×\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{Q}=\int\frac{\frac{{u}^{\mathrm{2}} +\mathrm{2}{u}+\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }}{\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }×\frac{\mathrm{2}}{\mathrm{1}+{u}^{\mathrm{2}} }}×\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{Q}=\int\frac{{u}^{\mathrm{2}} +\mathrm{2}{u}+\mathrm{1}}{\mathrm{2}{u}}{du} \\ $$$$\Rightarrow\:{Q}=\frac{\mathrm{1}}{\mathrm{4}}{u}^{\mathrm{2}} +{u}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{u}\mid+{C} \\ $$$$ \\ $$$$\therefore\because\:\:{Q}=\frac{\mathrm{1}}{\mathrm{4}}\left({tan}\left(\frac{{x}}{\mathrm{2}}\right)\right)^{\mathrm{2}} +{tan}\left(\frac{{x}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{tan}\left(\frac{{x}}{\mathrm{2}}\right)\mid+{C}.. \\ $$
Commented by ZiYangLee last updated on 12/Sep/21

$${thank}\:{you}\:{puissant}...{for}\:{always}\:{helping}\:{me}\:{on} \\ $$$${my}\:{integration}\:{problems}... \\ $$
Commented by puissant last updated on 12/Sep/21
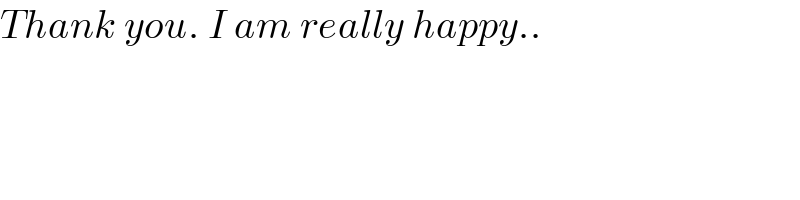
$${Thank}\:{you}.\:{I}\:{am}\:{really}\:{happy}.. \\ $$
