
Question Number 336 by Vishal Bhardwaj last updated on 25/Jan/15
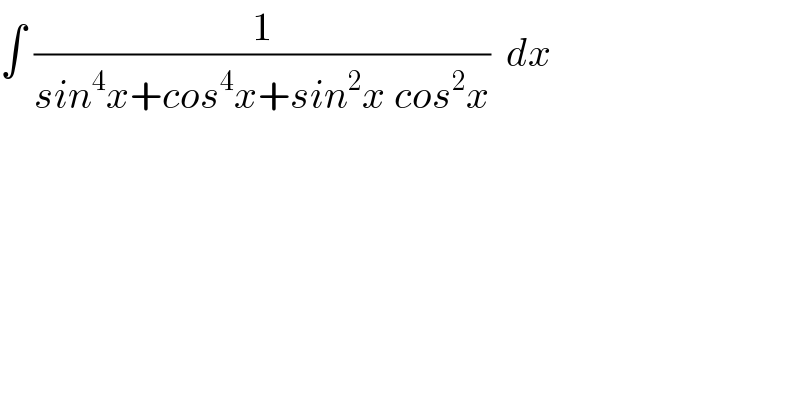
$$\int\:\frac{\mathrm{1}}{{sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}+{sin}^{\mathrm{2}} {x}\:{cos}^{\mathrm{2}} {x}}\:\:{dx} \\ $$
Commented by 123456 last updated on 22/Dec/14
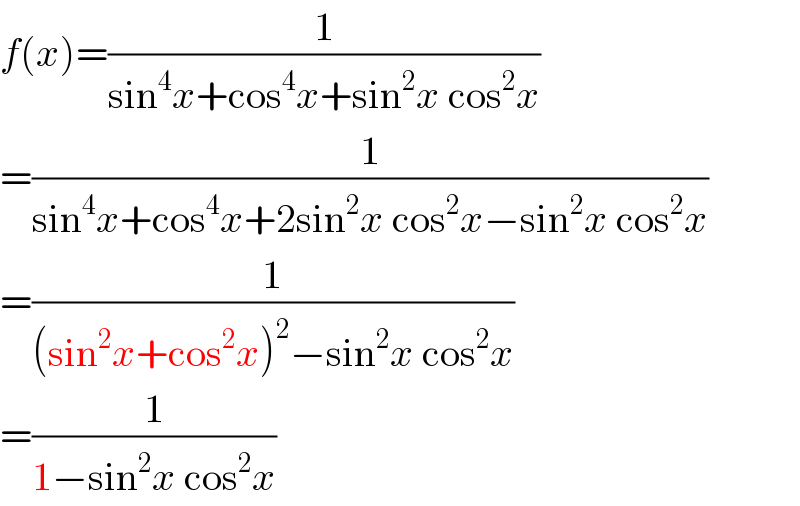
$${f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{4}} {x}+\mathrm{cos}^{\mathrm{4}} {x}+\mathrm{sin}^{\mathrm{2}} {x}\:\mathrm{cos}^{\mathrm{2}} {x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{4}} {x}+\mathrm{cos}^{\mathrm{4}} {x}+\mathrm{2sin}^{\mathrm{2}} {x}\:\mathrm{cos}^{\mathrm{2}} {x}−\mathrm{sin}^{\mathrm{2}} {x}\:\mathrm{cos}^{\mathrm{2}} {x}} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{sin}^{\mathrm{2}} {x}+\mathrm{cos}^{\mathrm{2}} {x}\right)^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} {x}\:\mathrm{cos}^{\mathrm{2}} {x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} {x}\:\mathrm{cos}^{\mathrm{2}} {x}} \\ $$
Commented by 123456 last updated on 23/Dec/14
![((tan^(−1) [((√3)/2)tan(2x)])/(√3))](Q345.png)
$$\frac{\mathrm{tan}^{−\mathrm{1}} \left[\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{tan}\left(\mathrm{2}{x}\right)\right]}{\sqrt{\mathrm{3}}} \\ $$
Answered by prakash jain last updated on 27/Dec/14
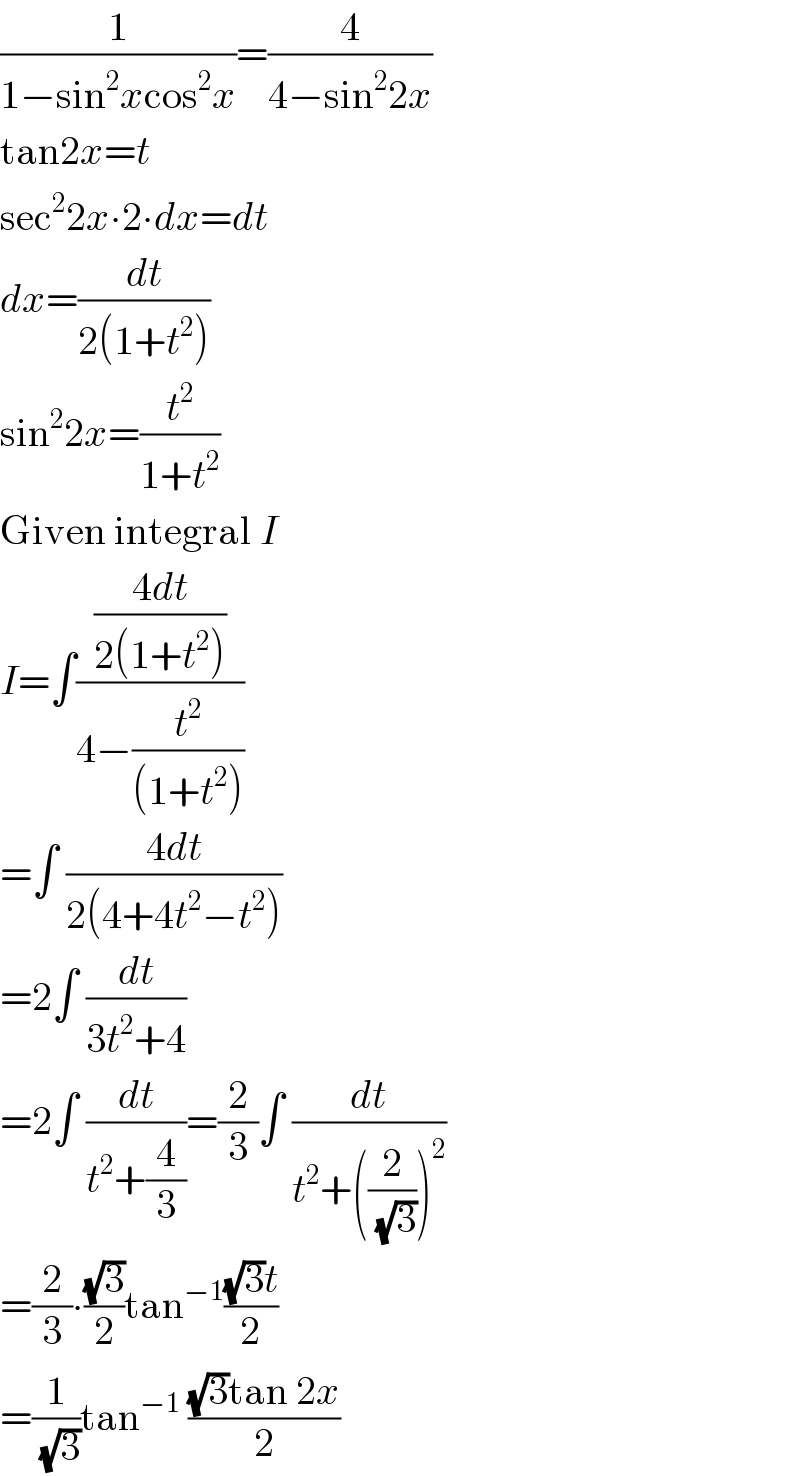
$$\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} {x}\mathrm{cos}^{\mathrm{2}} {x}}=\frac{\mathrm{4}}{\mathrm{4}−\mathrm{sin}^{\mathrm{2}} \mathrm{2}{x}} \\ $$$$\mathrm{tan2}{x}={t} \\ $$$$\mathrm{sec}^{\mathrm{2}} \mathrm{2}{x}\centerdot\mathrm{2}\centerdot{dx}={dt} \\ $$$${dx}=\frac{{dt}}{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$$\mathrm{sin}^{\mathrm{2}} \mathrm{2}{x}=\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\mathrm{Given}\:\mathrm{integral}\:{I} \\ $$$${I}=\int\frac{\frac{\mathrm{4}{dt}}{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}}{\mathrm{4}−\frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}} \\ $$$$=\int\:\frac{\mathrm{4}{dt}}{\mathrm{2}\left(\mathrm{4}+\mathrm{4}{t}^{\mathrm{2}} −{t}^{\mathrm{2}} \right)} \\ $$$$=\mathrm{2}\int\:\frac{{dt}}{\mathrm{3}{t}^{\mathrm{2}} +\mathrm{4}} \\ $$$$=\mathrm{2}\int\:\frac{{dt}}{{t}^{\mathrm{2}} +\frac{\mathrm{4}}{\mathrm{3}}}=\frac{\mathrm{2}}{\mathrm{3}}\int\:\frac{{dt}}{{t}^{\mathrm{2}} +\left(\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\centerdot\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}{t}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{3}}\mathrm{tan}\:\mathrm{2}{x}}{\mathrm{2}} \\ $$
