
Question Number 216990 by MathematicalUser2357 last updated on 26/Feb/25
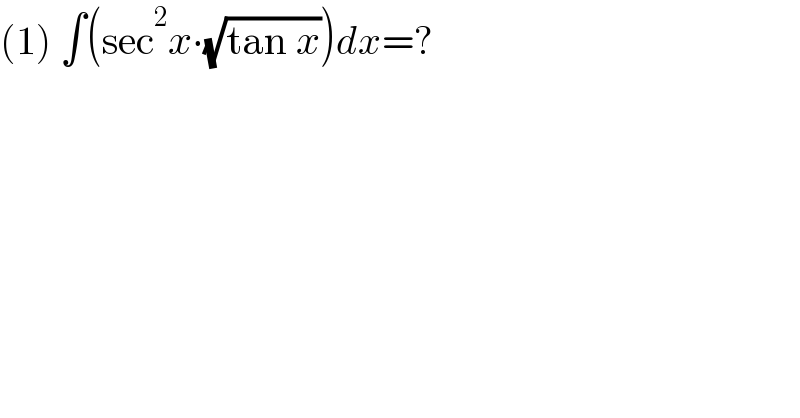
$$\left(\mathrm{1}\right)\:\int\left(\mathrm{sec}^{\mathrm{2}} {x}\centerdot\sqrt{\mathrm{tan}\:{x}}\right){dx}=? \\ $$
Answered by Frix last updated on 26/Feb/25
![∫sec^2 x (√(tan x)) dx =^([t=(√(tan x))]) 2∫t^2 dt=(2/3)t^3 = =(2/3)tan^(3/2) x +C](Q217003.png)
$$\int\mathrm{sec}^{\mathrm{2}} \:{x}\:\sqrt{\mathrm{tan}\:{x}}\:{dx}\:\overset{\left[{t}=\sqrt{\mathrm{tan}\:{x}}\right]} {=}\:\mathrm{2}\int{t}^{\mathrm{2}} {dt}=\frac{\mathrm{2}}{\mathrm{3}}{t}^{\mathrm{3}} = \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{tan}^{\frac{\mathrm{3}}{\mathrm{2}}} \:{x}\:+{C} \\ $$
Commented by MathematicalUser2357 last updated on 27/Feb/25
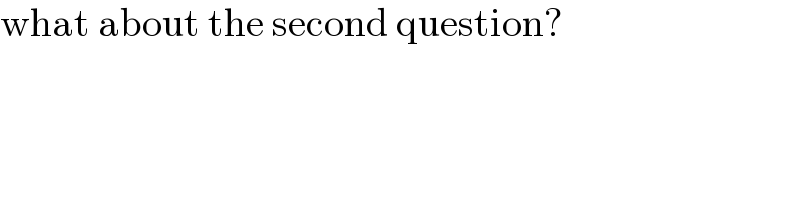
$$\mathrm{what}\:\mathrm{about}\:\mathrm{the}\:\mathrm{second}\:\mathrm{question}? \\ $$
Answered by MATHEMATICSAM last updated on 27/Feb/25
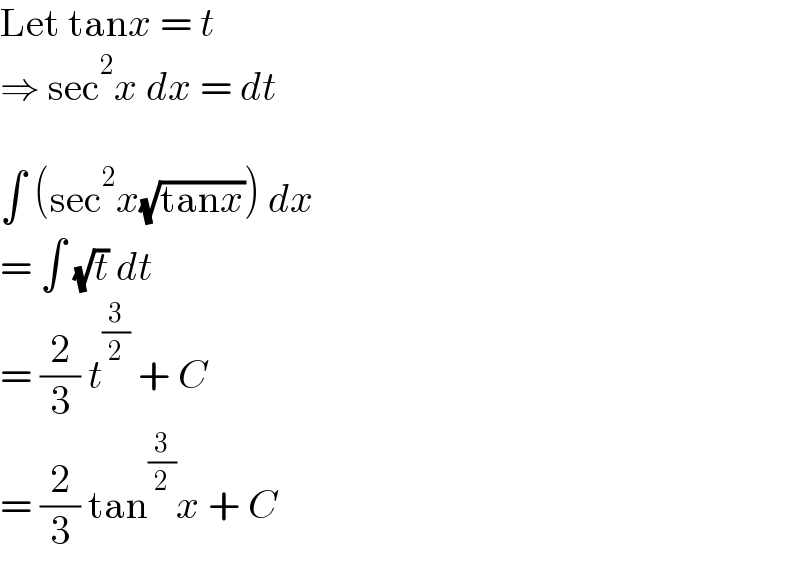
$$\mathrm{Let}\:\mathrm{tan}{x}\:=\:{t} \\ $$$$\Rightarrow\:\mathrm{sec}^{\mathrm{2}} {x}\:{dx}\:=\:{dt} \\ $$$$ \\ $$$$\int\:\left(\mathrm{sec}^{\mathrm{2}} {x}\sqrt{\mathrm{tan}{x}}\right)\:{dx} \\ $$$$=\:\int\:\sqrt{{t}}\:{dt} \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{3}}\:{t}^{\frac{\mathrm{3}}{\mathrm{2}}} \:+\:{C} \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{tan}^{\frac{\mathrm{3}}{\mathrm{2}}} {x}\:+\:{C} \\ $$
