
Question Number 199511 by SANOGO last updated on 04/Nov/23
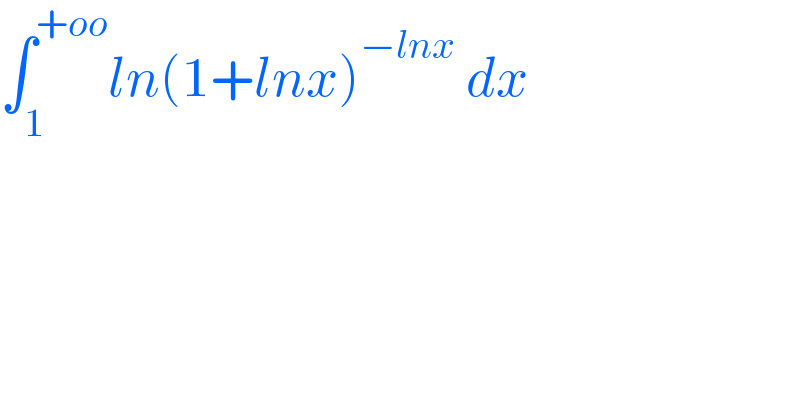
$$\int_{\mathrm{1}} ^{+{oo}} {ln}\left(\mathrm{1}+{lnx}\right)^{−{lnx}} \:{dx} \\ $$
Commented by SANOGO last updated on 04/Nov/23
$${thank}\:{you} \\ $$
Answered by witcher3 last updated on 04/Nov/23
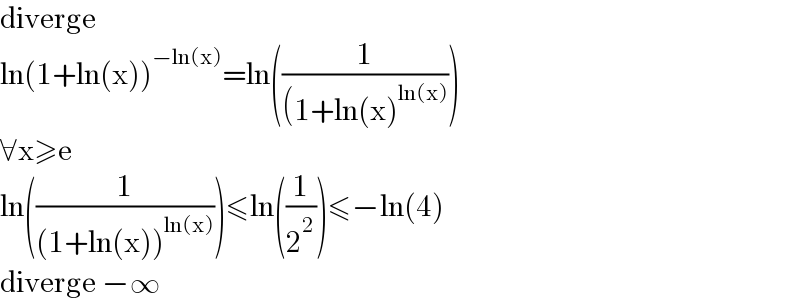
$$\mathrm{diverge} \\ $$$$\mathrm{ln}\left(\mathrm{1}+\mathrm{ln}\left(\mathrm{x}\right)\right)^{−\mathrm{ln}\left(\mathrm{x}\right)} =\mathrm{ln}\left(\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{ln}\left(\mathrm{x}\right)^{\mathrm{ln}\left(\mathrm{x}\right)} \right.}\right) \\ $$$$\forall\mathrm{x}\geqslant\mathrm{e} \\ $$$$\mathrm{ln}\left(\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{ln}\left(\mathrm{x}\right)\right)^{\mathrm{ln}\left(\mathrm{x}\right)} }\right)\leqslant\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)\leqslant−\mathrm{ln}\left(\mathrm{4}\right) \\ $$$$\mathrm{diverge}\:−\infty \\ $$
