
Previous in Relation and Functions Next in Relation and Functions
Question Number 180901 by alcohol last updated on 19/Nov/22
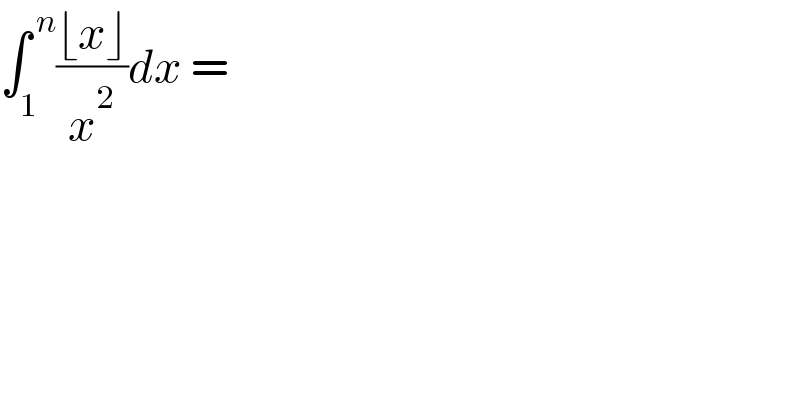
$$\int_{\mathrm{1}} ^{\:{n}} \frac{\lfloor{x}\rfloor}{{x}^{\mathrm{2}} }{dx}\:=\: \\ $$
Answered by srikanth2684 last updated on 19/Nov/22
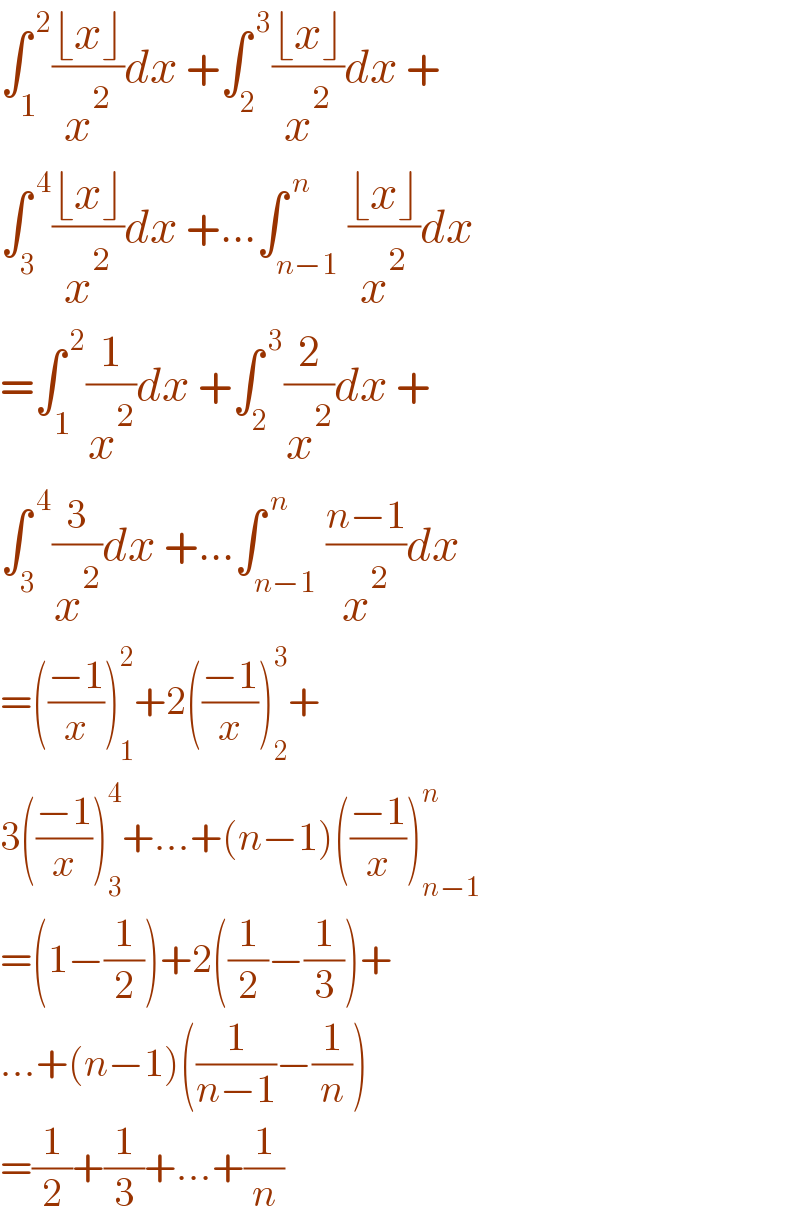
$$\int_{\mathrm{1}} ^{\:\mathrm{2}} \frac{\lfloor{x}\rfloor}{{x}^{\mathrm{2}} }{dx}\:+\int_{\mathrm{2}} ^{\:\mathrm{3}} \frac{\lfloor{x}\rfloor}{{x}^{\mathrm{2}} }{dx}\:+ \\ $$$$\int_{\mathrm{3}} ^{\:\mathrm{4}} \frac{\lfloor{x}\rfloor}{{x}^{\mathrm{2}} }{dx}\:+...\int_{{n}−\mathrm{1}} ^{\:{n}} \frac{\lfloor{x}\rfloor}{{x}^{\mathrm{2}} }{dx}\: \\ $$$$=\int_{\mathrm{1}} ^{\:\mathrm{2}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx}\:+\int_{\mathrm{2}} ^{\:\mathrm{3}} \frac{\mathrm{2}}{{x}^{\mathrm{2}} }{dx}\:+ \\ $$$$\int_{\mathrm{3}} ^{\:\mathrm{4}} \frac{\mathrm{3}}{{x}^{\mathrm{2}} }{dx}\:+...\int_{{n}−\mathrm{1}} ^{\:{n}} \frac{{n}−\mathrm{1}}{{x}^{\mathrm{2}} }{dx}\: \\ $$$$=\left(\frac{−\mathrm{1}}{{x}}\right)_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{2}\left(\frac{−\mathrm{1}}{{x}}\right)_{\mathrm{2}} ^{\mathrm{3}} + \\ $$$$\mathrm{3}\left(\frac{−\mathrm{1}}{{x}}\right)_{\mathrm{3}} ^{\mathrm{4}} +...+\left({n}−\mathrm{1}\right)\left(\frac{−\mathrm{1}}{{x}}\right)_{{n}−\mathrm{1}} ^{{n}} \\ $$$$=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\right)+ \\ $$$$...+\left({n}−\mathrm{1}\right)\left(\frac{\mathrm{1}}{{n}−\mathrm{1}}−\frac{\mathrm{1}}{{n}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+...+\frac{\mathrm{1}}{{n}} \\ $$
