
Question Number 46640 by canhtoan last updated on 29/Oct/18
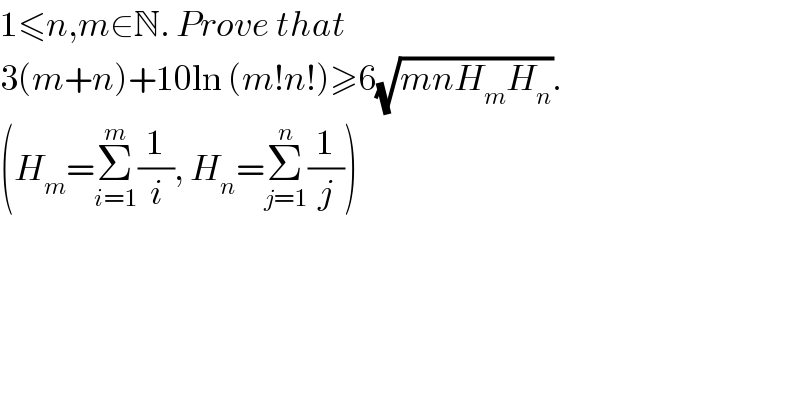
$$\mathrm{1}\leqslant{n},{m}\in\mathbb{N}.\:{Prove}\:{that} \\ $$$$\mathrm{3}\left({m}+{n}\right)+\mathrm{10ln}\:\left({m}!{n}!\right)\geqslant\mathrm{6}\sqrt{{mnH}_{{m}} {H}_{{n}} }. \\ $$$$\left({H}_{{m}} =\underset{{i}=\mathrm{1}} {\overset{{m}} {\sum}}\frac{\mathrm{1}}{{i}},\:{H}_{{n}} =\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{j}}\right) \\ $$
Commented by canhtoan last updated on 29/Oct/18

$${Help}\:{me} \\ $$
