Question and Answers Forum

All Questions      Topic List

Logarithms Questions

Previous in All Question      Next in All Question      

Previous in Logarithms      Next in Logarithms      

Question Number 95108 by bobhans last updated on 23/May/20

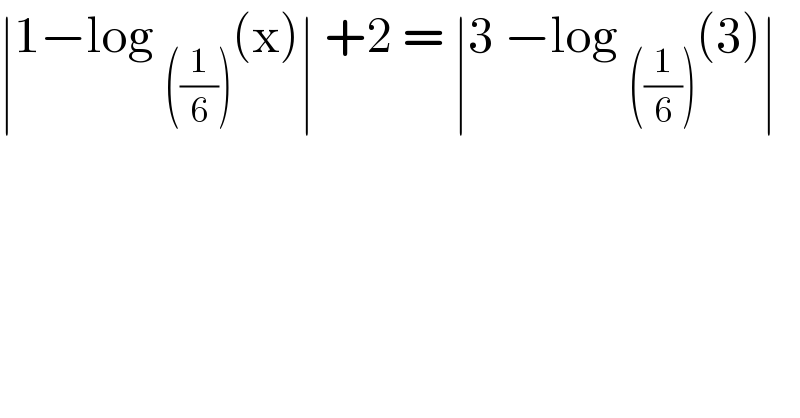
∣1−log _(((1/6))) (x)∣ +2 = ∣3 −log _(((1/6))) (3)∣

$$\mid\mathrm{1}−\mathrm{log}\:_{\left(\frac{\mathrm{1}}{\mathrm{6}}\right)} \left(\mathrm{x}\right)\mid\:+\mathrm{2}\:=\:\mid\mathrm{3}\:−\mathrm{log}\:_{\left(\frac{\mathrm{1}}{\mathrm{6}}\right)} \left(\mathrm{3}\right)\mid\: \\ $$

Answered by john santu last updated on 23/May/20

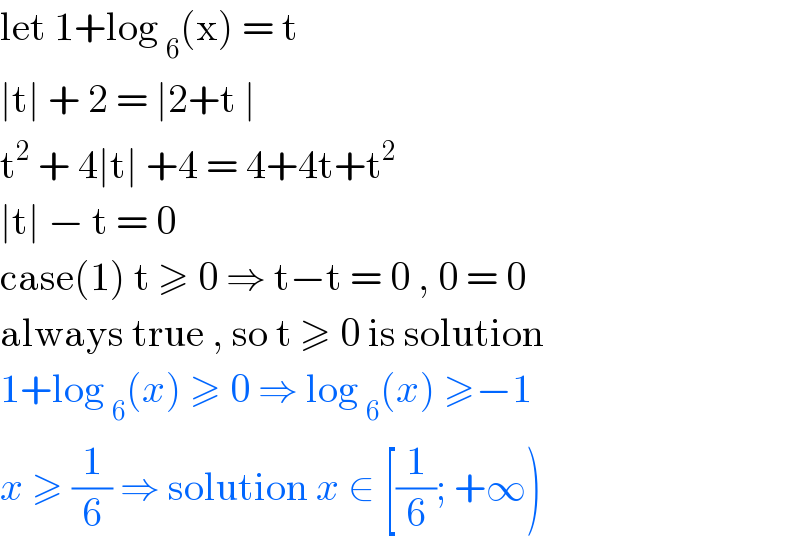
let 1+log _6 (x) = t ∣t∣ + 2 = ∣2+t ∣ t^2 + 4∣t∣ +4 = 4+4t+t^2 ∣t∣ − t = 0 case(1) t ≥ 0 ⇒ t−t = 0 , 0 = 0 always true , so t ≥ 0 is solution 1+log _6 (x) ≥ 0 ⇒ log _6 (x) ≥−1 x ≥ (1/6) ⇒ solution x ∈ [(1/6); +∞)

$$\mathrm{let}\:\mathrm{1}+\mathrm{log}\:_{\mathrm{6}} \left(\mathrm{x}\right)\:=\:\mathrm{t}\: \\ $$$$\mid\mathrm{t}\mid\:+\:\mathrm{2}\:=\:\mid\mathrm{2}+\mathrm{t}\:\mid \\ $$$$\mathrm{t}^{\mathrm{2}} \:+\:\mathrm{4}\mid\mathrm{t}\mid\:+\mathrm{4}\:=\:\mathrm{4}+\mathrm{4t}+\mathrm{t}^{\mathrm{2}} \\ $$$$\mid\mathrm{t}\mid\:−\:\mathrm{t}\:=\:\mathrm{0} \\ $$$$\mathrm{case}\left(\mathrm{1}\right)\:\mathrm{t}\:\geqslant\:\mathrm{0}\:\Rightarrow\:\mathrm{t}−\mathrm{t}\:=\:\mathrm{0}\:,\:\mathrm{0}\:=\:\mathrm{0} \\ $$$$\mathrm{always}\:\mathrm{true}\:,\:\mathrm{so}\:\mathrm{t}\:\geqslant\:\mathrm{0}\:\mathrm{is}\:\mathrm{solution} \\ $$$$\mathrm{1}+\mathrm{log}\:_{\mathrm{6}} \left({x}\right)\:\geqslant\:\mathrm{0}\:\Rightarrow\:\mathrm{log}\:_{\mathrm{6}} \left({x}\right)\:\geqslant−\mathrm{1} \\ $$$${x}\:\geqslant\:\frac{\mathrm{1}}{\mathrm{6}}\:\Rightarrow\:\mathrm{solution}\:{x}\:\in\:\left[\frac{\mathrm{1}}{\mathrm{6}};\:+\infty\right)\: \\ $$

Commented by bobhans last updated on 23/May/20

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com