
Question Number 112273 by bemath last updated on 07/Sep/20
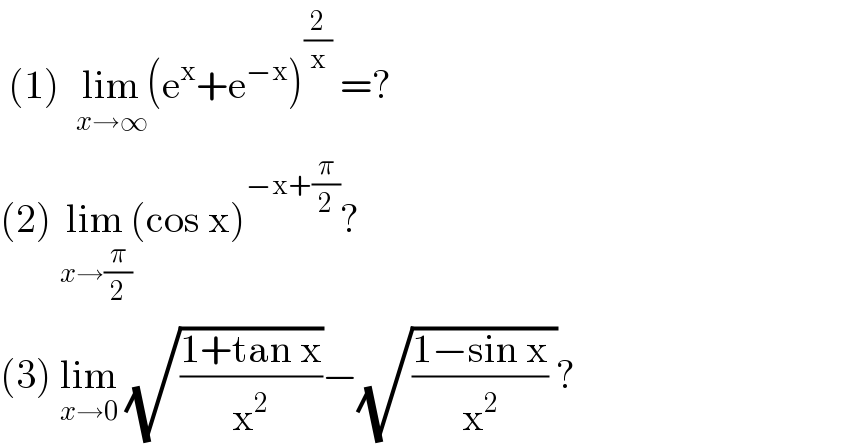
$$\:\left(\mathrm{1}\right)\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{−\mathrm{x}} \right)^{\frac{\mathrm{2}}{\mathrm{x}}} \:=? \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\left(\mathrm{cos}\:\mathrm{x}\right)^{−\mathrm{x}+\frac{\pi}{\mathrm{2}}} ? \\ $$$$\left(\mathrm{3}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt{\frac{\mathrm{1}+\mathrm{tan}\:\mathrm{x}}{\mathrm{x}^{\mathrm{2}} }}−\sqrt{\frac{\mathrm{1}−\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{2}} }\:}? \\ $$
Commented by Dwaipayan Shikari last updated on 07/Sep/20
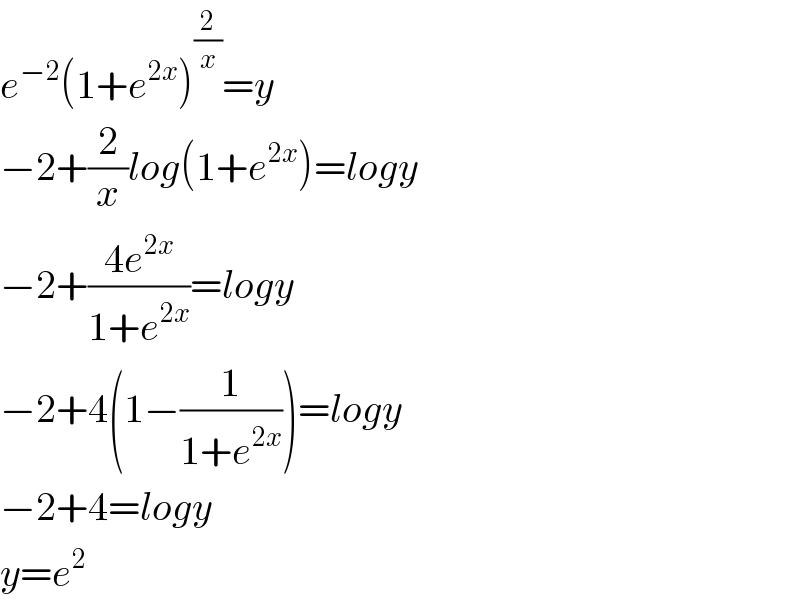
$${e}^{−\mathrm{2}} \left(\mathrm{1}+{e}^{\mathrm{2}{x}} \right)^{\frac{\mathrm{2}}{{x}}} ={y} \\ $$$$−\mathrm{2}+\frac{\mathrm{2}}{{x}}{log}\left(\mathrm{1}+{e}^{\mathrm{2}{x}} \right)={logy} \\ $$$$−\mathrm{2}+\frac{\mathrm{4}{e}^{\mathrm{2}{x}} }{\mathrm{1}+{e}^{\mathrm{2}{x}} }={logy} \\ $$$$−\mathrm{2}+\mathrm{4}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{e}^{\mathrm{2}{x}} }\right)={logy} \\ $$$$−\mathrm{2}+\mathrm{4}={logy} \\ $$$${y}={e}^{\mathrm{2}} \\ $$
Commented by Dwaipayan Shikari last updated on 07/Sep/20
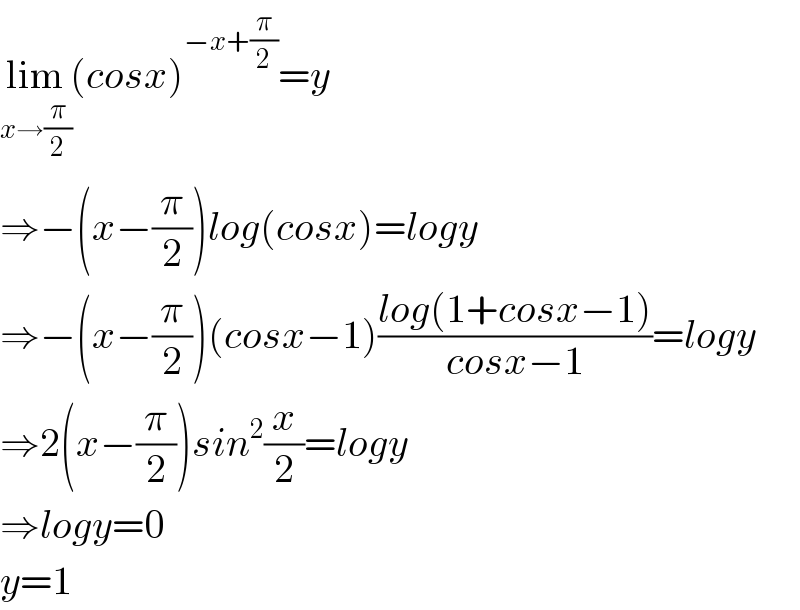
$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\left({cosx}\right)^{−{x}+\frac{\pi}{\mathrm{2}}} ={y} \\ $$$$\Rightarrow−\left({x}−\frac{\pi}{\mathrm{2}}\right){log}\left({cosx}\right)={logy} \\ $$$$\Rightarrow−\left({x}−\frac{\pi}{\mathrm{2}}\right)\left({cosx}−\mathrm{1}\right)\frac{{log}\left(\mathrm{1}+{cosx}−\mathrm{1}\right)}{{cosx}−\mathrm{1}}={logy} \\ $$$$\Rightarrow\mathrm{2}\left({x}−\frac{\pi}{\mathrm{2}}\right){sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}={logy} \\ $$$$\Rightarrow{logy}=\mathrm{0} \\ $$$${y}=\mathrm{1} \\ $$
Answered by bemath last updated on 07/Sep/20
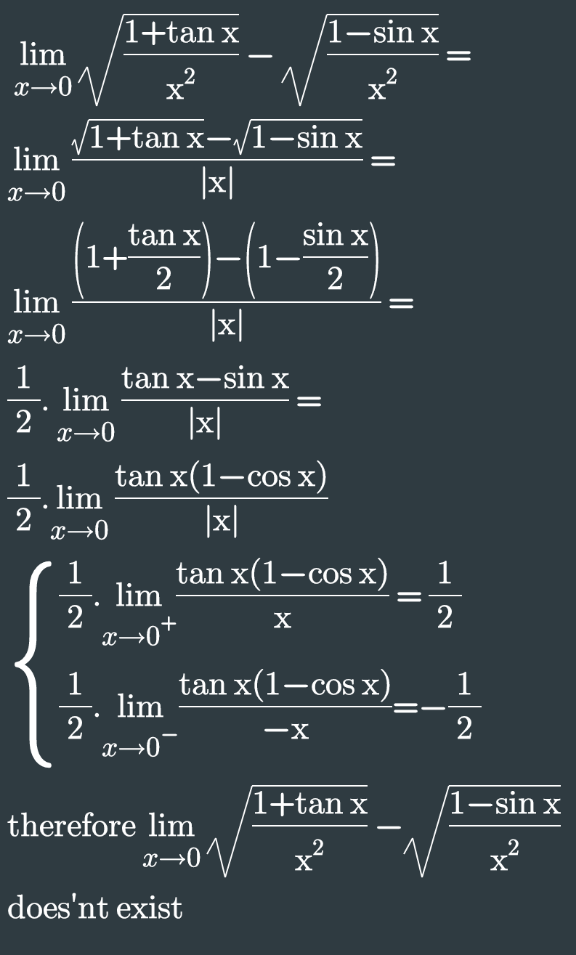
Commented by mohammad17 last updated on 07/Sep/20
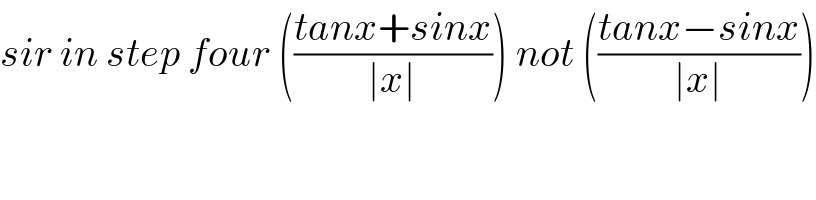
$${sir}\:{in}\:{step}\:{four}\:\left(\frac{{tanx}+{sinx}}{\mid{x}\mid}\right)\:{not}\:\left(\frac{{tanx}−{sinx}}{\mid{x}\mid}\right) \\ $$
Commented by bemath last updated on 07/Sep/20
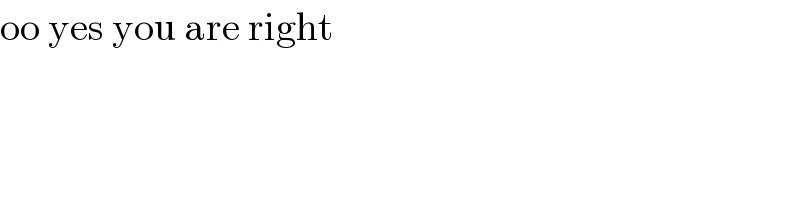
$$\mathrm{oo}\:\mathrm{yes}\:\mathrm{you}\:\mathrm{are}\:\mathrm{right} \\ $$
