
Question Number 110307 by bemath last updated on 28/Aug/20
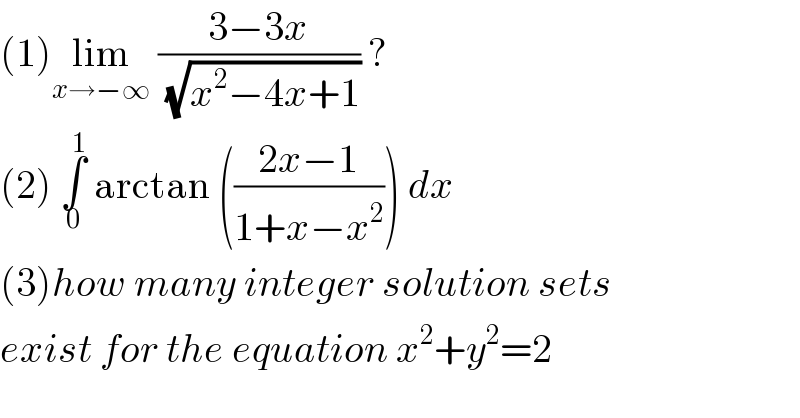
$$\left(\mathrm{1}\right)\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{\mathrm{3}−\mathrm{3}{x}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}}}\:? \\ $$$$\left(\mathrm{2}\right)\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\mathrm{arctan}\:\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{1}+{x}−{x}^{\mathrm{2}} }\right)\:{dx} \\ $$$$\left(\mathrm{3}\right){how}\:{many}\:{integer}\:{solution}\:{sets} \\ $$$${exist}\:{for}\:{the}\:{equation}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{2} \\ $$
Answered by john santu last updated on 28/Aug/20
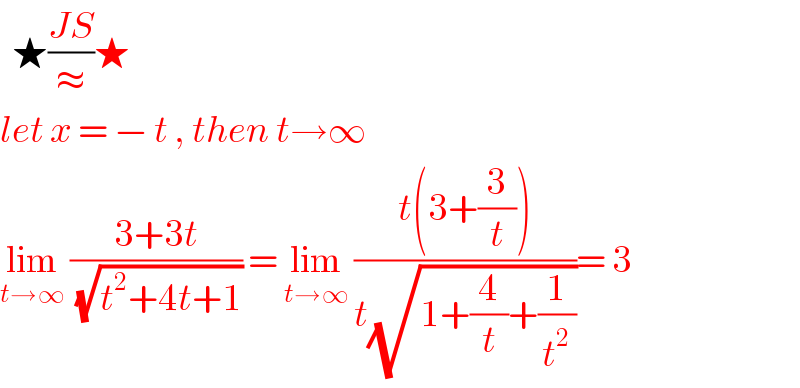
$$\:\:\bigstar\frac{{JS}}{\approx}\bigstar \\ $$$${let}\:{x}\:=\:−\:{t}\:,\:{then}\:{t}\rightarrow\infty \\ $$$$\underset{{t}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{3}+\mathrm{3}{t}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{4}{t}+\mathrm{1}}}\:=\:\underset{{t}\rightarrow\infty} {\mathrm{lim}}\:\frac{{t}\left(\mathrm{3}+\frac{\mathrm{3}}{{t}}\right)}{{t}\sqrt{\mathrm{1}+\frac{\mathrm{4}}{{t}}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}}=\:\mathrm{3} \\ $$
Answered by Dwaipayan Shikari last updated on 28/Aug/20
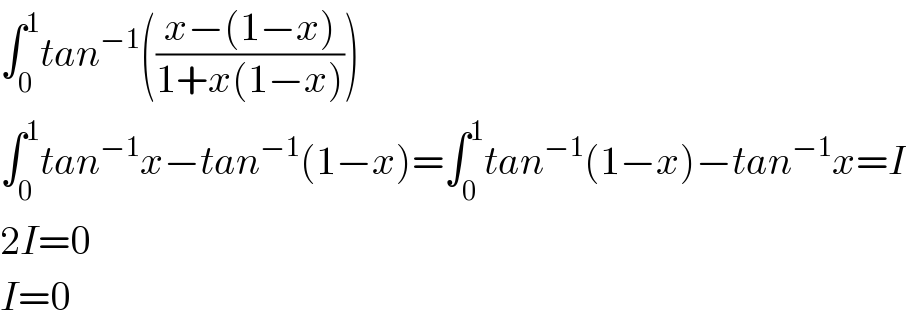
$$\int_{\mathrm{0}} ^{\mathrm{1}} {tan}^{−\mathrm{1}} \left(\frac{{x}−\left(\mathrm{1}−{x}\right)}{\mathrm{1}+{x}\left(\mathrm{1}−{x}\right)}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {tan}^{−\mathrm{1}} {x}−{tan}^{−\mathrm{1}} \left(\mathrm{1}−{x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {tan}^{−\mathrm{1}} \left(\mathrm{1}−{x}\right)−{tan}^{−\mathrm{1}} {x}={I} \\ $$$$\mathrm{2}{I}=\mathrm{0} \\ $$$${I}=\mathrm{0} \\ $$
Commented by Dwaipayan Shikari last updated on 28/Aug/20

$${Is}\:{it}\:{right}? \\ $$
Answered by Aziztisffola last updated on 28/Aug/20
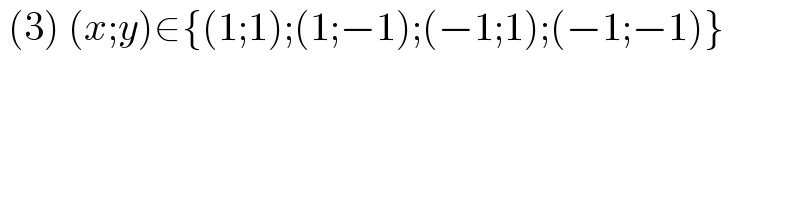
$$\:\left(\mathrm{3}\right)\:\left({x};{y}\right)\in\left\{\left(\mathrm{1};\mathrm{1}\right);\left(\mathrm{1};−\mathrm{1}\right);\left(−\mathrm{1};\mathrm{1}\right);\left(−\mathrm{1};−\mathrm{1}\right)\right\} \\ $$
Answered by Rio Michael last updated on 28/Aug/20
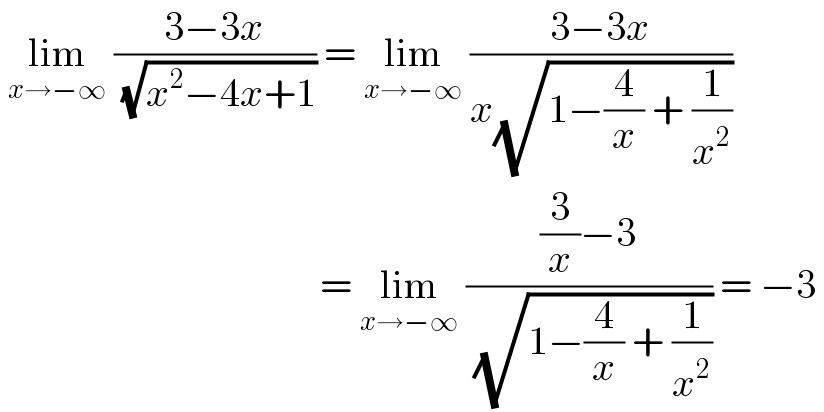
$$\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{\mathrm{3}−\mathrm{3}{x}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}}}\:=\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{\mathrm{3}−\mathrm{3}{x}}{{x}\sqrt{\mathrm{1}−\frac{\mathrm{4}}{{x}}\:+\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{\frac{\mathrm{3}}{{x}}−\mathrm{3}}{\:\sqrt{\mathrm{1}−\frac{\mathrm{4}}{{x}}\:+\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}}\:=\:−\mathrm{3}\: \\ $$
Commented by bemath last updated on 28/Aug/20
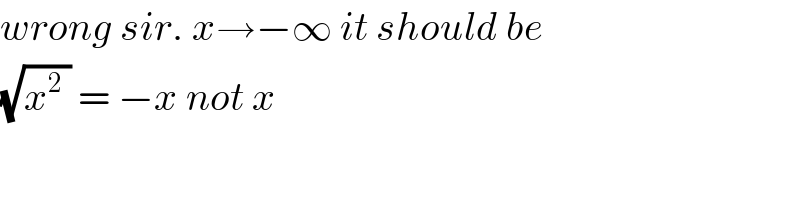
$${wrong}\:{sir}.\:{x}\rightarrow−\infty\:{it}\:{should}\:{be}\: \\ $$$$\sqrt{{x}^{\mathrm{2}} \:}\:=\:−{x}\:{not}\:{x}\: \\ $$
Commented by Rio Michael last updated on 28/Aug/20
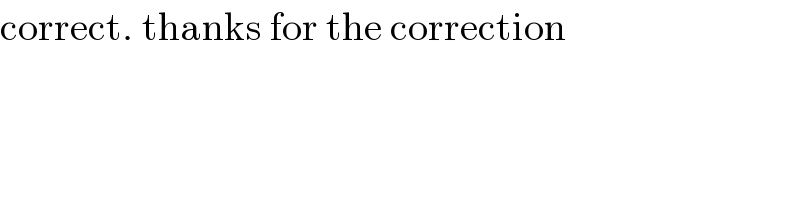
$$\mathrm{correct}.\:\mathrm{thanks}\:\mathrm{for}\:\mathrm{the}\:\mathrm{correction} \\ $$
Answered by 1549442205PVT last updated on 28/Aug/20

$$\left(\mathrm{1}\right)\underset{\mathrm{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{\mathrm{3}−\mathrm{3}{x}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}}}\:=\underset{\mathrm{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{\mathrm{3}−\mathrm{3x}}{\:\left(−\mathrm{x}\:\right)\:\:\sqrt{\mathrm{1}−\frac{\mathrm{4}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}} \\ $$$$=\underset{\mathrm{x}\rightarrow−\infty} {\mathrm{lim}}\:\frac{\frac{−\mathrm{3}}{\mathrm{x}}+\mathrm{3}}{\:\sqrt{\mathrm{1}−\frac{\mathrm{4}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}}=\frac{\mathrm{0}+\mathrm{3}}{\:\sqrt{\mathrm{1}−\mathrm{0}+\mathrm{0}}}=\mathrm{3} \\ $$$$\left.\mathrm{3}\right)\mathrm{Solve}\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{2}\:\mathrm{in}\:\mathbb{Z}. \\ $$$$\mathrm{x}^{\mathrm{2}} =\mathrm{2}−\mathrm{y}^{\mathrm{2}} \leqslant\mathrm{2}\:\mathrm{but}\:\mathrm{since}\:\mathrm{x}\in\mathbb{Z},\mid\mathrm{x}\mid\leqslant\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}\in−\mathrm{1},\mathrm{1}\Rightarrow\mathrm{y}\in\left\{\pm\mathrm{1},\pm\mathrm{1}\right\} \\ $$$$\:\mathrm{The}\:\mathrm{solution}\:\mathrm{set}\:\mathrm{of}\:\mathrm{the}\:\mathrm{given}\:\mathrm{eq}. \\ $$$$\mathrm{has}\:\mathrm{four}\:\mathrm{elements} \\ $$$$\mathrm{S}=\left\{\left(−\mathrm{1},−\mathrm{1}\right),\left(−\mathrm{1},\mathrm{1}\right),\left(\mathrm{1},−\mathrm{1}\right),\left(\mathrm{1},\mathrm{1}\right)\right\} \\ $$
Answered by john santu last updated on 28/Aug/20

$$\left(\mathrm{2}\right)\int\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{1}+{x}−{x}^{\mathrm{2}} }\right)\:{dx}\:=\:{I} \\ $$$${setting}\:{x}\:=\:{u}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${I}=\underset{−\mathrm{1}/\mathrm{2}} {\overset{\mathrm{1}/\mathrm{2}} {\int}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{u}}{\frac{\mathrm{5}}{\mathrm{4}}−{u}^{\mathrm{2}} }\right)\:{du}\: \\ $$$${since}\:{the}\:{resulting}\:{integrand}\:{is} \\ $$$${a}\:{continous}\:{odd}\:{function}\:,\:{so}\:{we}\:{got} \\ $$$${I}\:=\:\mathrm{0}. \\ $$
