
Question Number 113274 by bemath last updated on 12/Sep/20
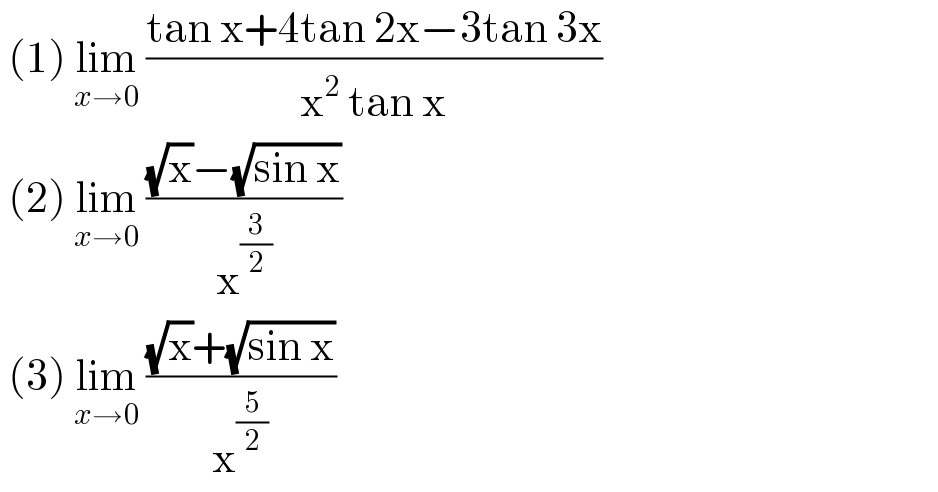
$$\:\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\mathrm{x}+\mathrm{4tan}\:\mathrm{2x}−\mathrm{3tan}\:\mathrm{3x}}{\mathrm{x}^{\mathrm{2}} \:\mathrm{tan}\:\mathrm{x}} \\ $$$$\:\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{x}}−\sqrt{\mathrm{sin}\:\mathrm{x}}}{\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }\: \\ $$$$\:\left(\mathrm{3}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{x}}+\sqrt{\mathrm{sin}\:\mathrm{x}}}{\mathrm{x}^{\frac{\mathrm{5}}{\mathrm{2}}} } \\ $$
Commented by bemath last updated on 12/Sep/20

Commented by bobhans last updated on 13/Sep/20
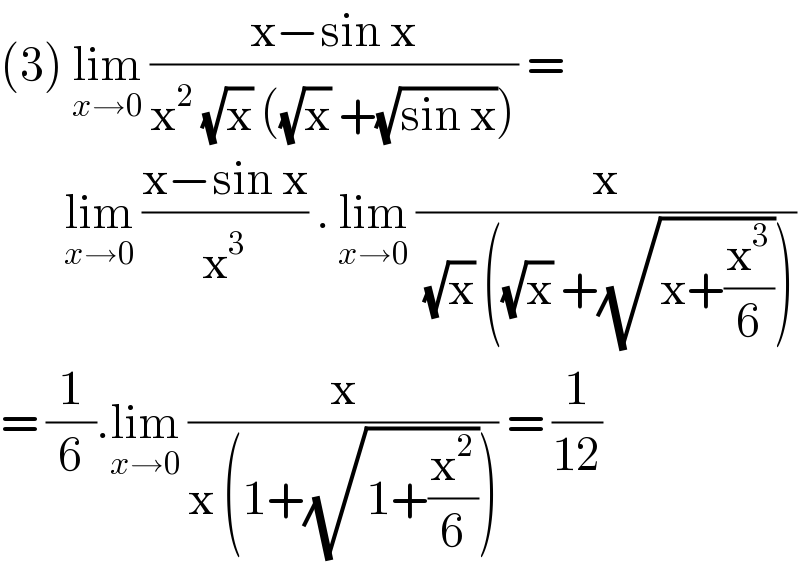
$$\left(\mathrm{3}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:\sqrt{\mathrm{x}}\:\left(\sqrt{\mathrm{x}}\:+\sqrt{\mathrm{sin}\:\mathrm{x}}\right)}\:= \\ $$$$\:\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{3}} }\:.\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}}{\:\sqrt{\mathrm{x}}\:\left(\sqrt{\mathrm{x}}\:+\sqrt{\mathrm{x}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}}\right)} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{6}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}}{\mathrm{x}\:\left(\mathrm{1}+\sqrt{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{12}} \\ $$
Answered by john santu last updated on 12/Sep/20
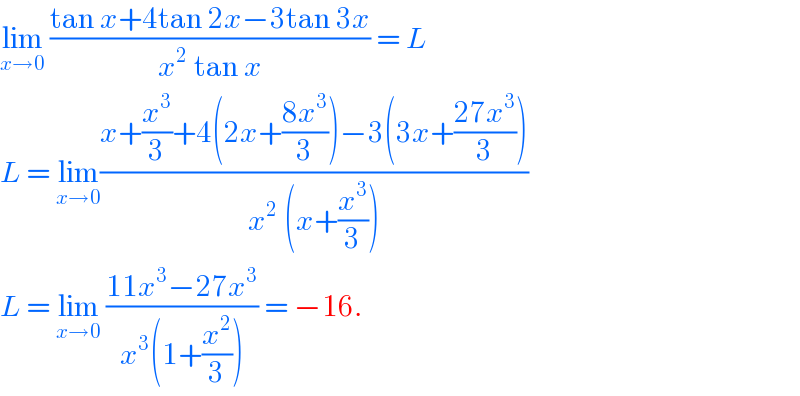
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:{x}+\mathrm{4tan}\:\mathrm{2}{x}−\mathrm{3tan}\:\mathrm{3}{x}}{{x}^{\mathrm{2}} \:\mathrm{tan}\:{x}}\:=\:{L} \\ $$$${L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{4}\left(\mathrm{2}{x}+\frac{\mathrm{8}{x}^{\mathrm{3}} }{\mathrm{3}}\right)−\mathrm{3}\left(\mathrm{3}{x}+\frac{\mathrm{27}{x}^{\mathrm{3}} }{\mathrm{3}}\right)}{{x}^{\mathrm{2}} \:\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)} \\ $$$${L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{11}{x}^{\mathrm{3}} −\mathrm{27}{x}^{\mathrm{3}} }{{x}^{\mathrm{3}} \left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}\right)}\:=\:−\mathrm{16}. \\ $$
Answered by Dwaipayan Shikari last updated on 12/Sep/20
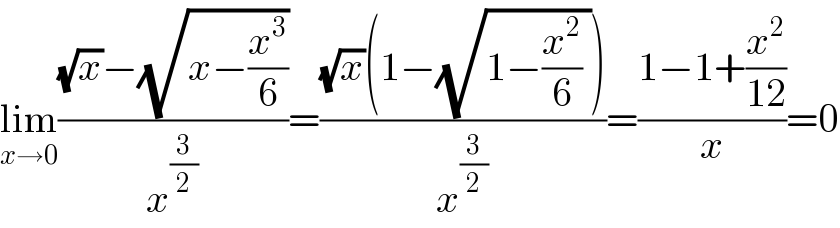
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{{x}}−\sqrt{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}}{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }=\frac{\sqrt{{x}}\left(\mathrm{1}−\sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\:}\right)}{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }=\frac{\mathrm{1}−\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{12}}}{{x}}=\mathrm{0} \\ $$
Answered by bemath last updated on 12/Sep/20
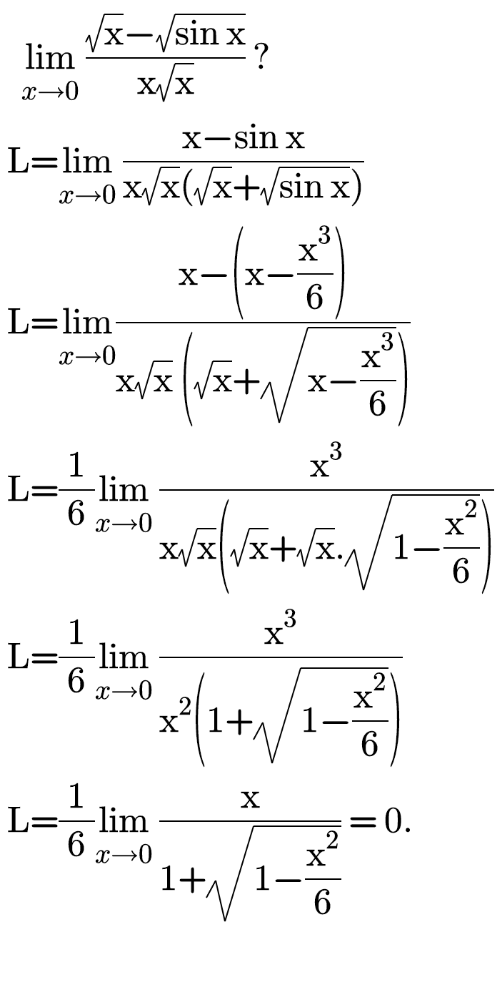
Answered by abdomsup last updated on 12/Sep/20
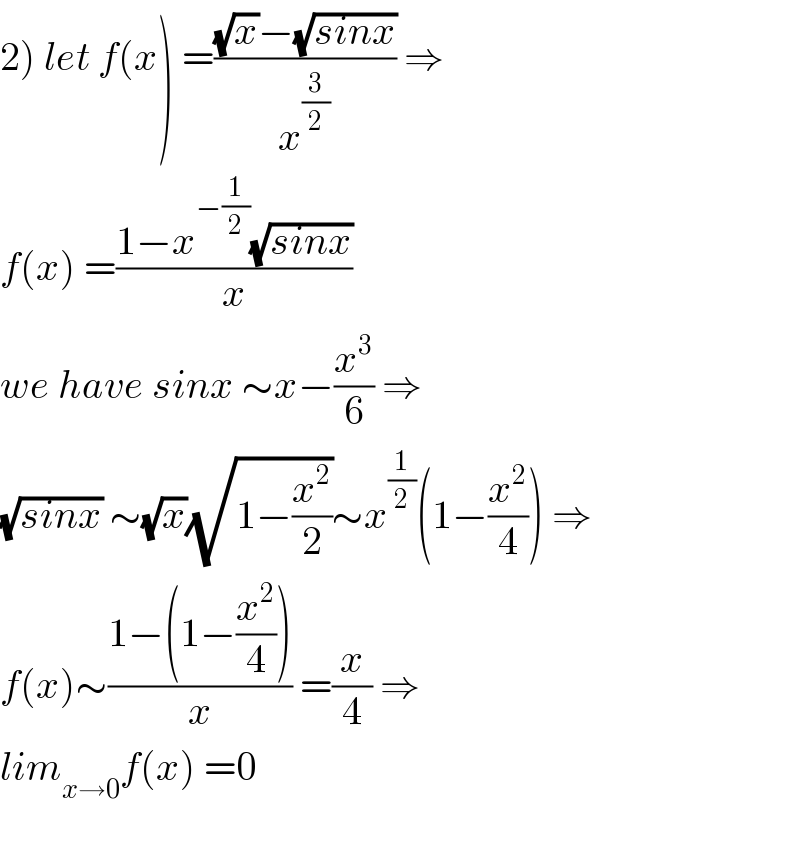
$$\left.\mathrm{2}\right)\:{let}\:{f}\left({x}\right)\:=\frac{\sqrt{{x}}−\sqrt{{sinx}}}{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:\Rightarrow \\ $$$${f}\left({x}\right)\:=\frac{\mathrm{1}−{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} \sqrt{{sinx}}}{{x}} \\ $$$${we}\:{have}\:{sinx}\:\sim{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\:\Rightarrow \\ $$$$\sqrt{{sinx}}\:\sim\sqrt{{x}}\sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}\sim{x}^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\right)\:\Rightarrow \\ $$$${f}\left({x}\right)\sim\frac{\mathrm{1}−\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\right)}{{x}}\:=\frac{{x}}{\mathrm{4}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} {f}\left({x}\right)\:=\mathrm{0} \\ $$$$ \\ $$
