
Question Number 118427 by bramlexs22 last updated on 17/Oct/20

$$\:\:\:\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt[{{x}^{\mathrm{2}} \:}]{\mathrm{cos}\:{x}}\: \\ $$$$\:\:\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{1}+\mathrm{cos}\:\pi{x}}{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}} \\ $$
Answered by Dwaipayan Shikari last updated on 17/Oct/20
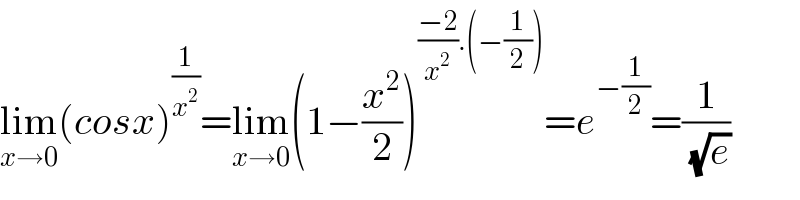
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({cosx}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} =\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)^{\frac{−\mathrm{2}}{{x}^{\mathrm{2}} }.\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)} ={e}^{−\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{1}}{\:\sqrt{{e}}} \\ $$
Commented by Dwaipayan Shikari last updated on 17/Oct/20
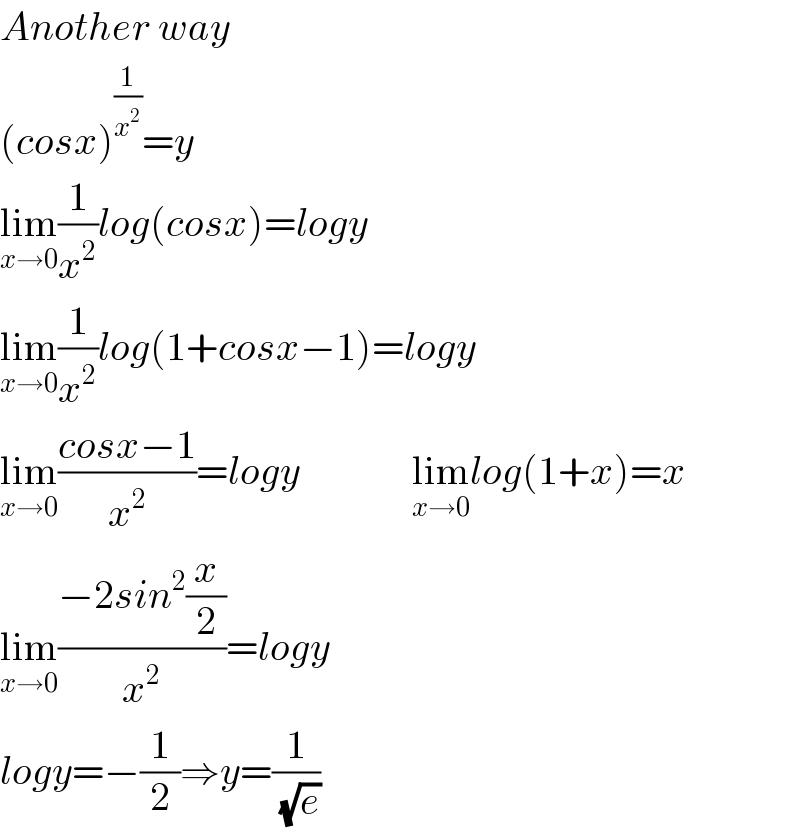
$${Another}\:{way} \\ $$$$\left({cosx}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} ={y} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{log}\left({cosx}\right)={logy} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{log}\left(\mathrm{1}+{cosx}−\mathrm{1}\right)={logy} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{cosx}−\mathrm{1}}{{x}^{\mathrm{2}} }={logy}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{log}\left(\mathrm{1}+{x}\right)={x} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{{x}^{\mathrm{2}} }={logy} \\ $$$${logy}=−\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow{y}=\frac{\mathrm{1}}{\:\sqrt{{e}}} \\ $$
Answered by Dwaipayan Shikari last updated on 17/Oct/20
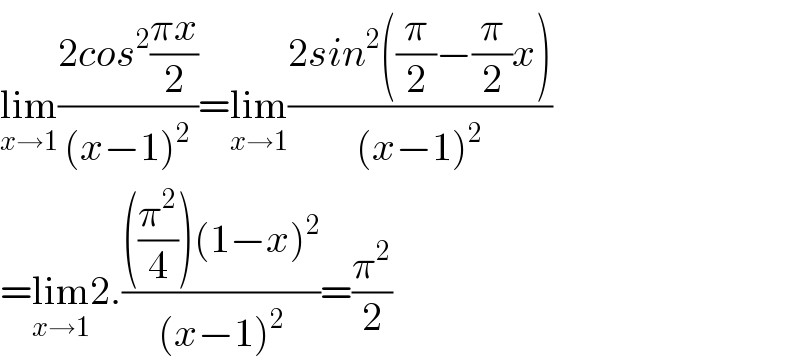
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{2}{cos}^{\mathrm{2}} \frac{\pi{x}}{\mathrm{2}}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{2}}{x}\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}2}.\frac{\left(\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\right)\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{2}} \\ $$
Answered by TANMAY PANACEA last updated on 17/Oct/20
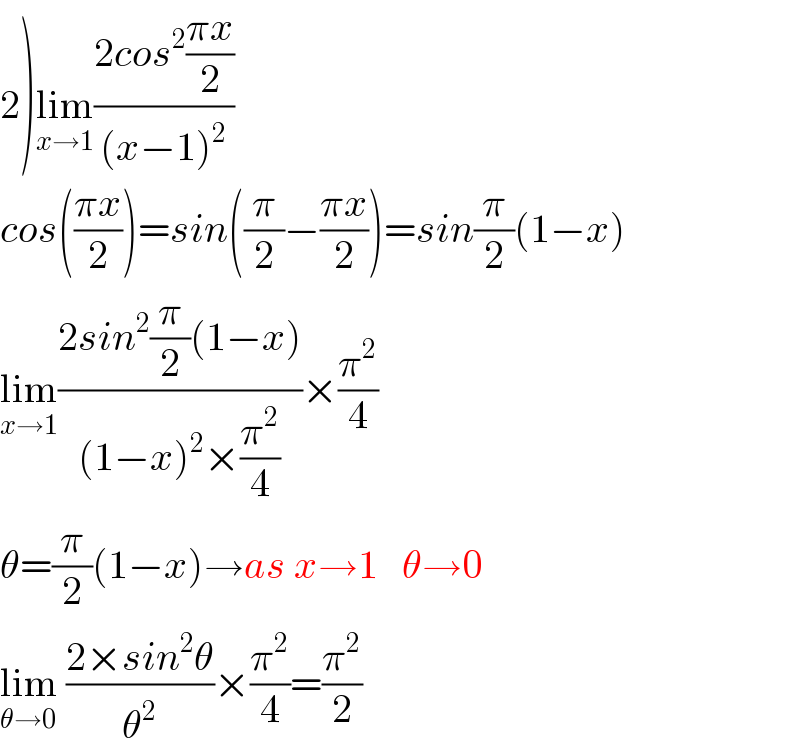
$$\left.\mathrm{2}\right)\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{2}{cos}^{\mathrm{2}} \frac{\pi{x}}{\mathrm{2}}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${cos}\left(\frac{\pi{x}}{\mathrm{2}}\right)={sin}\left(\frac{\pi}{\mathrm{2}}−\frac{\pi{x}}{\mathrm{2}}\right)={sin}\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−{x}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{2}{sin}^{\mathrm{2}} \frac{\pi}{\mathrm{2}}\left(\mathrm{1}−{x}\right)}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} ×\frac{\pi^{\mathrm{2}} }{\mathrm{4}}}×\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\theta=\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−{x}\right)\rightarrow{as}\:{x}\rightarrow\mathrm{1}\:\:\:\theta\rightarrow\mathrm{0} \\ $$$$\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}×{sin}^{\mathrm{2}} \theta}{\theta^{\mathrm{2}} }×\frac{\pi^{\mathrm{2}} }{\mathrm{4}}=\frac{\pi^{\mathrm{2}} }{\mathrm{2}} \\ $$
Answered by benjo_mathlover last updated on 17/Oct/20

$$\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt[{{x}^{\mathrm{2}\:} }]{\mathrm{cos}\:{x}}\:=\:{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{cos}\:{x}−\mathrm{1}}{{x}^{\mathrm{2}} }\right)} ={e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} −\mathrm{1}\right).\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \\ $$$$=\:{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} =\:\frac{\mathrm{1}}{\:\sqrt{{e}}}\: \\ $$
Answered by benjo_mathlover last updated on 17/Oct/20
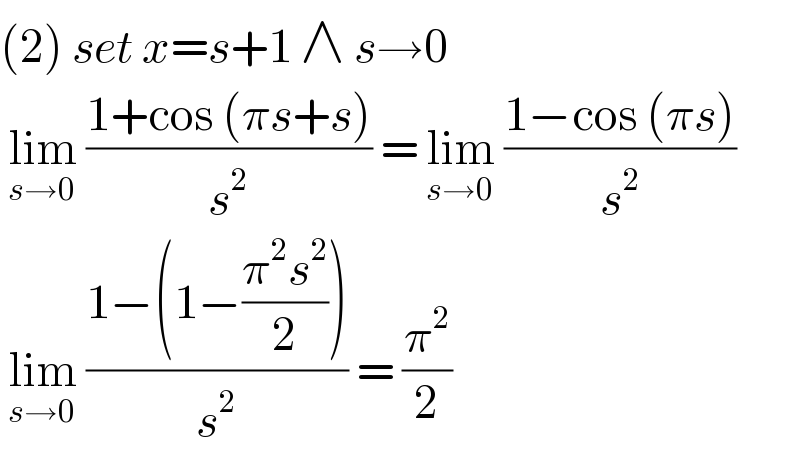
$$\left(\mathrm{2}\right)\:{set}\:{x}={s}+\mathrm{1}\:\wedge\:{s}\rightarrow\mathrm{0} \\ $$$$\:\underset{{s}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}+\mathrm{cos}\:\left(\pi{s}+{s}\right)}{{s}^{\mathrm{2}} }\:=\:\underset{{s}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:\left(\pi{s}\right)}{{s}^{\mathrm{2}} } \\ $$$$\:\underset{{s}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\left(\mathrm{1}−\frac{\pi^{\mathrm{2}} {s}^{\mathrm{2}} }{\mathrm{2}}\right)}{{s}^{\mathrm{2}} }\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{2}} \\ $$
Answered by Bird last updated on 17/Oct/20
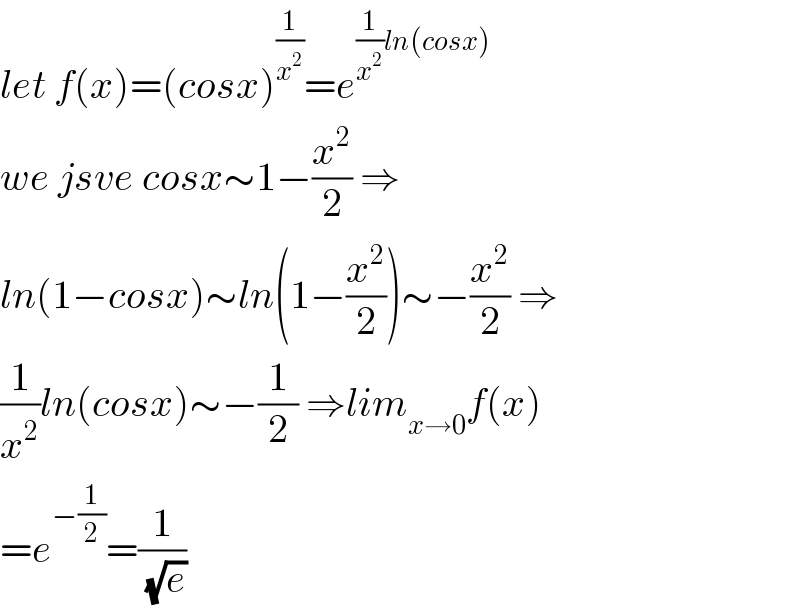
$${let}\:{f}\left({x}\right)=\left({cosx}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} ={e}^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{ln}\left({cosx}\right)} \\ $$$${we}\:{jsve}\:{cosx}\sim\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}−{cosx}\right)\sim{ln}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\sim−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{ln}\left({cosx}\right)\sim−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} {f}\left({x}\right) \\ $$$$={e}^{−\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{1}}{\:\sqrt{{e}}} \\ $$
Answered by mathmax by abdo last updated on 17/Oct/20
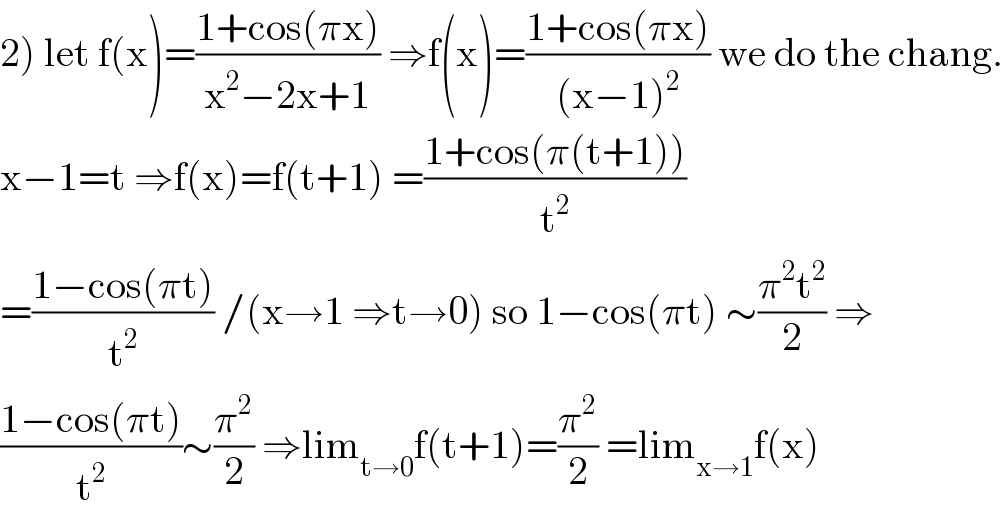
$$\left.\mathrm{2}\right)\:\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}+\mathrm{cos}\left(\pi\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}+\mathrm{cos}\left(\pi\mathrm{x}\right)}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{chang}. \\ $$$$\mathrm{x}−\mathrm{1}=\mathrm{t}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{t}+\mathrm{1}\right)\:=\frac{\mathrm{1}+\mathrm{cos}\left(\pi\left(\mathrm{t}+\mathrm{1}\right)\right)}{\mathrm{t}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}−\mathrm{cos}\left(\pi\mathrm{t}\right)}{\mathrm{t}^{\mathrm{2}} }\:/\left(\mathrm{x}\rightarrow\mathrm{1}\:\Rightarrow\mathrm{t}\rightarrow\mathrm{0}\right)\:\mathrm{so}\:\mathrm{1}−\mathrm{cos}\left(\pi\mathrm{t}\right)\:\sim\frac{\pi^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\frac{\mathrm{1}−\mathrm{cos}\left(\pi\mathrm{t}\right)}{\mathrm{t}^{\mathrm{2}} }\sim\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\mathrm{lim}_{\mathrm{t}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{t}+\mathrm{1}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \mathrm{f}\left(\mathrm{x}\right) \\ $$
