Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 125056 by benjo_mathlover last updated on 08/Dec/20

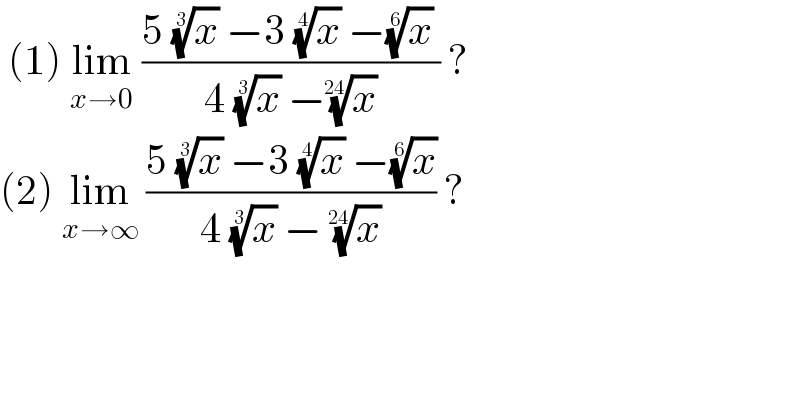
(1) lim_(x→0) ((5 (x)^(1/3) −3 (x)^(1/4) −(x)^(1/6) )/(4 (x)^(1/3) −(x)^(1/(24)) )) ? (2) lim_(x→∞) ((5 (x)^(1/3) −3 (x)^(1/4) −(x)^(1/6) )/(4 (x)^(1/3) − (x)^(1/(24)) )) ?

$$\:\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{5}\:\sqrt[{\mathrm{3}}]{{x}}\:−\mathrm{3}\:\sqrt[{\mathrm{4}}]{{x}}\:−\sqrt[{\mathrm{6}}]{{x}}\:}{\mathrm{4}\:\sqrt[{\mathrm{3}}]{{x}}\:−\sqrt[{\mathrm{24}}]{{x}}}\:? \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{5}\:\sqrt[{\mathrm{3}}]{{x}}\:−\mathrm{3}\:\sqrt[{\mathrm{4}}]{{x}}\:−\sqrt[{\mathrm{6}}]{{x}}}{\mathrm{4}\:\sqrt[{\mathrm{3}}]{{x}}\:−\:\sqrt[{\mathrm{24}}]{{x}}}\:?\: \\ $$

Answered by bramlexs22 last updated on 08/Dec/20

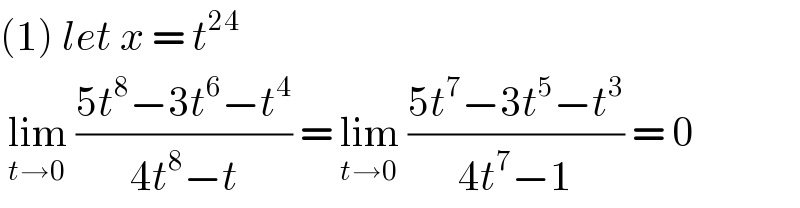
(1) let x = t^(24) lim_(t→0) ((5t^8 −3t^6 −t^4 )/(4t^8 −t)) = lim_(t→0) ((5t^7 −3t^5 −t^3 )/(4t^7 −1)) = 0

$$\left(\mathrm{1}\right)\:{let}\:{x}\:=\:{t}^{\mathrm{24}} \\ $$$$\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{5}{t}^{\mathrm{8}} −\mathrm{3}{t}^{\mathrm{6}} −{t}^{\mathrm{4}} }{\mathrm{4}{t}^{\mathrm{8}} −{t}}\:=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{5}{t}^{\mathrm{7}} −\mathrm{3}{t}^{\mathrm{5}} −{t}^{\mathrm{3}} }{\mathrm{4}{t}^{\mathrm{7}} −\mathrm{1}}\:=\:\mathrm{0} \\ $$

Commented by bramlexs22 last updated on 08/Dec/20

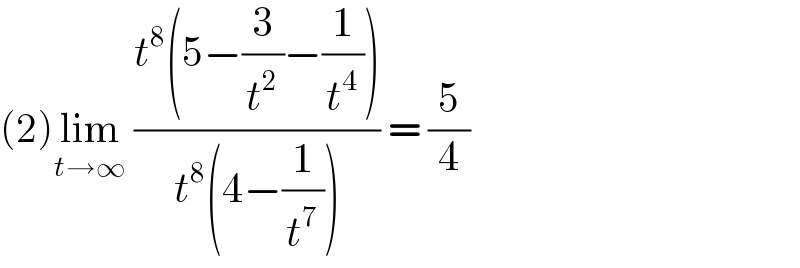
(2)lim_(t→∞) ((t^8 (5−(3/t^2 )−(1/t^4 )))/(t^8 (4−(1/t^7 )))) = (5/4)

$$\left(\mathrm{2}\right)\underset{{t}\rightarrow\infty} {\mathrm{lim}}\:\frac{{t}^{\mathrm{8}} \left(\mathrm{5}−\frac{\mathrm{3}}{{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{{t}^{\mathrm{4}} }\right)}{{t}^{\mathrm{8}} \left(\mathrm{4}−\frac{\mathrm{1}}{{t}^{\mathrm{7}} }\right)}\:=\:\frac{\mathrm{5}}{\mathrm{4}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com