
Question Number 182200 by Shrinava last updated on 05/Dec/22
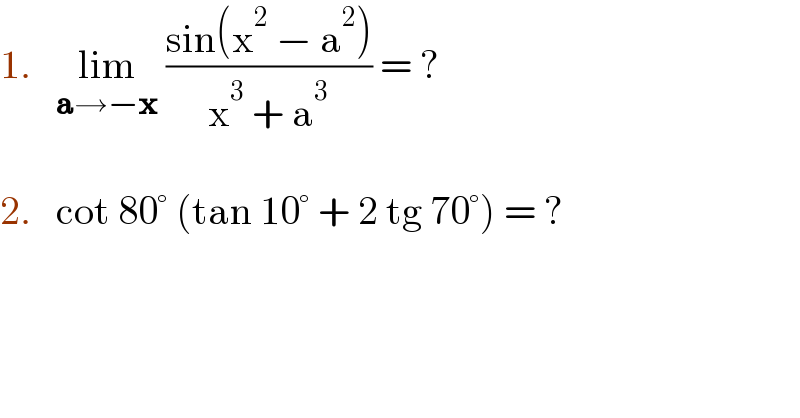
$$\mathrm{1}.\:\:\:\underset{\boldsymbol{\mathrm{a}}\rightarrow−\boldsymbol{\mathrm{x}}} {\mathrm{lim}}\:\frac{\mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{a}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{a}^{\mathrm{3}} }\:=\:? \\ $$$$ \\ $$$$\mathrm{2}.\:\:\:\mathrm{cot}\:\mathrm{80}°\:\left(\mathrm{tan}\:\mathrm{10}°\:+\:\mathrm{2}\:\mathrm{tg}\:\mathrm{70}°\right)\:=\:? \\ $$
Answered by cortano1 last updated on 06/Dec/22

$$\mathrm{1}.\:\underset{\mathrm{a}\rightarrow−\mathrm{x}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\mathrm{x}+\mathrm{a}\right)\left(\mathrm{x}−\mathrm{a}\right)}{\left(\mathrm{x}+\mathrm{a}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{ax}+\mathrm{a}^{\mathrm{2}} \right)} \\ $$$$\:=\:\frac{\mathrm{2x}}{\mathrm{3x}^{\mathrm{2}} }\:=\:\frac{\mathrm{2}}{\mathrm{3x}} \\ $$
Answered by som(math1967) last updated on 06/Dec/22

$$\mathrm{2}.\:{tan}\mathrm{80}=\frac{{tan}\mathrm{70}+{tan}\mathrm{10}}{\mathrm{1}−{tan}\mathrm{70}{tan}\mathrm{10}} \\ $$$$\:\Rightarrow{tan}\mathrm{80}−{tan}\mathrm{70}.{tan}\mathrm{10}.{tan}\mathrm{80} \\ $$$$\:\:\:\:\:\:={tan}\mathrm{70}+{tan}\mathrm{10} \\ $$$$\Rightarrow{tan}\mathrm{80}−{tan}\mathrm{70}.{tan}\mathrm{10}.{cot}\mathrm{10} \\ $$$$\:\:\:\:={tan}\mathrm{70}+{tan}\mathrm{10} \\ $$$$\Rightarrow{tan}\mathrm{80}−{tan}\mathrm{10}=\mathrm{2}{tan}\mathrm{70} \\ $$$${now}\:{cot}\mathrm{80}\left({tan}\mathrm{10}+\mathrm{2}{tan}\mathrm{70}\right) \\ $$$$={cot}\mathrm{80}\left({tan}\mathrm{10}+{tan}\mathrm{80}−{tan}\mathrm{10}\right) \\ $$$$={cot}\mathrm{80}×{tan}\mathrm{80}=\mathrm{1}\:{ans} \\ $$$$ \\ $$
