
Question Number 33894 by math khazana by abdo last updated on 26/Apr/18
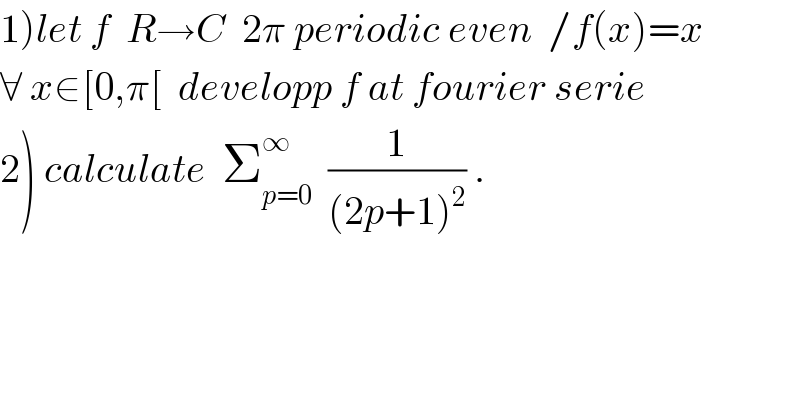
$$\left.\mathrm{1}\right){let}\:{f}\:\:{R}\rightarrow{C}\:\:\mathrm{2}\pi\:{periodic}\:{even}\:\:/{f}\left({x}\right)={x}\: \\ $$$$\forall\:{x}\in\left[\mathrm{0},\pi\left[\:\:{developp}\:{f}\:{at}\:{fourier}\:{serie}\right.\right. \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\:\sum_{{p}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{p}+\mathrm{1}\right)^{\mathrm{2}} }\:. \\ $$
Commented by abdo imad last updated on 28/Apr/18
![f is even so f(x)=(a_0 /2) +Σ_(n=1) ^∞ a_n cos(nx)with a_n = (2/T) ∫_([T]) f(x)cos(nx)dx=(2/(2π)) ∫_(−π) ^π x cos(nx)dx =(2/π) ∫_0 ^π xcos(nx)dx⇒ (π/2)a_n =∫_0 ^π xcos(nx)dx let integrate by parts u^ =x and v^′ =cos(nx)⇒ (π/2)a_n =((x/n)sin(nx)]_0 ^π −∫_0 ^π (1/n)sin(nx)dx =−(1/n)∫_0 ^π sin(nx)=(1/n^2 )[cos(nx)]_0 ^π =(1/n^2 )((−1)^n −1) ⇒ a_n =(2/(πn^2 ))((−1)^n −1)⇒a_(2n) =0 and a_(2n+1) =((−4)/(π(2n+1)^2 )) (π/2)a_0 =∫_0 ^π xdx=(π^2 /2) ⇒a_0 =π ⇒ f(x) = (π/2) −(4/π) Σ_(n=0) ^∞ ((cos(2n+1)x)/((2n+1)^2 )) (d) 2) let take x=0 in (d) we get 0=(π/2) −(4/π) Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒(4/π) Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(π/2) ⇒ Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(π^2 /8) .](Q33973.png)
$${f}\:{is}\:{even}\:{so}\:{f}\left({x}\right)=\frac{{a}_{\mathrm{0}} }{\mathrm{2}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:{a}_{{n}} {cos}\left({nx}\right){with} \\ $$$${a}_{{n}} =\:\frac{\mathrm{2}}{{T}}\:\int_{\left[{T}\right]} {f}\left({x}\right){cos}\left({nx}\right){dx}=\frac{\mathrm{2}}{\mathrm{2}\pi}\:\int_{−\pi} ^{\pi} \:{x}\:{cos}\left({nx}\right){dx} \\ $$$$=\frac{\mathrm{2}}{\pi}\:\int_{\mathrm{0}} ^{\pi} \:{xcos}\left({nx}\right){dx}\Rightarrow\:\frac{\pi}{\mathrm{2}}{a}_{{n}} =\int_{\mathrm{0}} ^{\pi} \:{xcos}\left({nx}\right){dx}\:{let}\:{integrate} \\ $$$${by}\:{parts}\:{u}^{} ={x}\:{and}\:{v}^{'} ={cos}\left({nx}\right)\Rightarrow \\ $$$$\frac{\pi}{\mathrm{2}}{a}_{{n}} =\left(\frac{{x}}{{n}}{sin}\left({nx}\right)\right]_{\mathrm{0}} ^{\pi} \:−\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{1}}{{n}}{sin}\left({nx}\right){dx} \\ $$$$=−\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\pi} {sin}\left({nx}\right)=\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\left[{cos}\left({nx}\right)\right]_{\mathrm{0}} ^{\pi} =\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\left(\left(−\mathrm{1}\right)^{{n}} \:−\mathrm{1}\right)\:\Rightarrow \\ $$$${a}_{{n}} =\frac{\mathrm{2}}{\pi{n}^{\mathrm{2}} }\left(\left(−\mathrm{1}\right)^{{n}} −\mathrm{1}\right)\Rightarrow{a}_{\mathrm{2}{n}} \:=\mathrm{0}\:{and}\:{a}_{\mathrm{2}{n}+\mathrm{1}} =\frac{−\mathrm{4}}{\pi\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\frac{\pi}{\mathrm{2}}{a}_{\mathrm{0}} =\int_{\mathrm{0}} ^{\pi} {xdx}=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow{a}_{\mathrm{0}} \:=\pi\:\Rightarrow \\ $$$${f}\left({x}\right)\:=\:\frac{\pi}{\mathrm{2}}\:−\frac{\mathrm{4}}{\pi}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{{cos}\left(\mathrm{2}{n}+\mathrm{1}\right){x}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\:\left({d}\right) \\ $$$$\left.\mathrm{2}\right)\:{let}\:{take}\:{x}=\mathrm{0}\:{in}\:\left({d}\right)\:{we}\:{get} \\ $$$$\mathrm{0}=\frac{\pi}{\mathrm{2}}\:−\frac{\mathrm{4}}{\pi}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\frac{\mathrm{4}}{\pi}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:. \\ $$
