
Previous in Relation and Functions Next in Relation and Functions
Question Number 32287 by abdo imad last updated on 22/Mar/18
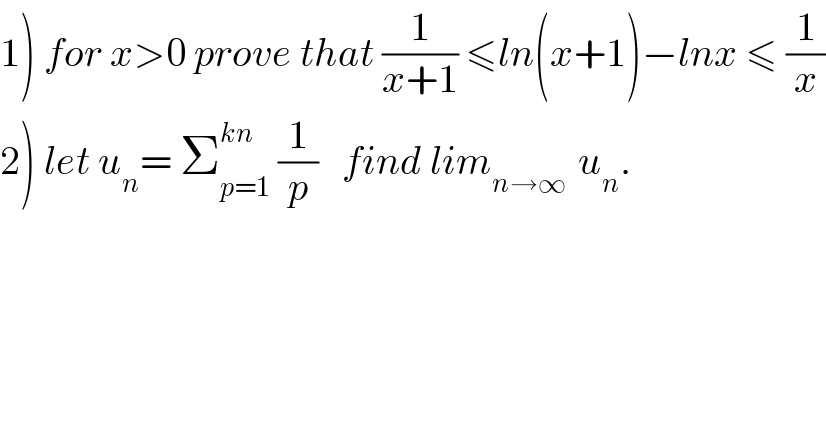
$$\left.\mathrm{1}\right)\:{for}\:{x}>\mathrm{0}\:{prove}\:{that}\:\frac{\mathrm{1}}{{x}+\mathrm{1}}\:\leqslant{ln}\left({x}+\mathrm{1}\right)−{lnx}\:\leqslant\:\frac{\mathrm{1}}{{x}} \\ $$$$\left.\mathrm{2}\right)\:{let}\:{u}_{{n}} =\:\sum_{{p}=\mathrm{1}} ^{{kn}} \:\frac{\mathrm{1}}{{p}}\:\:\:{find}\:{lim}_{{n}\rightarrow\infty\:} \:{u}_{{n}} . \\ $$
