
Question Number 36938 by maxmathsup by imad last updated on 07/Jun/18
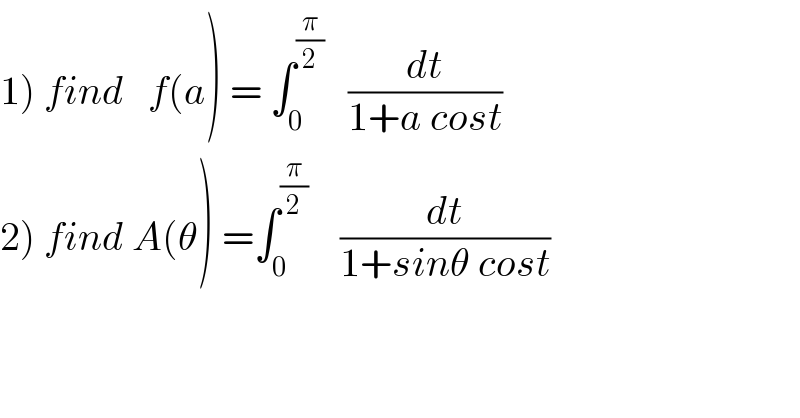
$$\left.\mathrm{1}\right)\:{find}\:\:\:{f}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{dt}}{\mathrm{1}+{a}\:{cost}} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{A}\left(\theta\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{{dt}}{\mathrm{1}+{sin}\theta\:{cost}} \\ $$
Commented by math khazana by abdo last updated on 09/Jun/18
![1) changemnt tan((t/2)) =x give f(a) = ∫_0 ^1 (1/(1+a ((1−x^2 )/(1+x^2 )))) ((2dx)/(1+x^2 )) = 2 ∫_0 ^1 (dx/(1+x^2 +a −ax^2 )) = 2 ∫_0 ^1 (dx/((1−a)x^2 +1+a)) = (2/(1−a))∫_0 ^1 (dx/(x^2 +((1+a)/(1−a)))) case1 ((1+a)/(1−a))> o ⇒∣a∣<1 we get by chang.x=(√((1+a)/(1−a))) u f(a) = (2/(1−a)) ∫_0 ^(√((1−a)/(1+a))) (1/(((1+a)/(1−a))(1+u^2 ))) (√((1+a)/(1−a))) du = (2/(1−a)) ((√(1−a))/(√(1+a))) [arctan(u)]_0 ^(√((1−a)/(1+a))) = (2/(√(1−a^2 ))) arctan((√((1−a)/(1+a)))) case 2 if ((1+a)/(1−a))<0 ⇒ ∣a∣>1 ∫_0 ^1 (dx/(x^2 +((1+a)/(1−a)))) =∫_0 ^1 (dx/(x^2 −((a+1)/(a−1)))) =_(x =(√((a+1)/(a−1))) u) ∫_0 ^(√((a−1)/(a+1))) (1/(((a+1)/(a−1))(u^2 −1))) (√((a+1)/(a−1))) du =(1/2)((√(a−1))/(√(a+1))) ∫_0 ^(√((a−1)/(a+1))) { (1/(u−1)) −(1/(u+1))}du = ((√(a−1))/(2(√(a+1)))) [ln∣((u−1)/(u+1))∣]_0 ^(√((a−1)/(a+1))) =((√(a−1))/(2(√(a+1)))) ln∣ (((√((a−1)/(a+1))) −1)/((√((a−1)/(a+1))) +1))∣ ⇒ f(a) = (2/(1−a)) ((√(a−1))/(2(√(a+1)))) ln∣ (((√((a−1)/(a+1))) −1)/((√((a−1)/(a+1))) +1))∣ = ((−1)/(√(a^2 −1)))ln∣ (((√((a−1)/(a+1))) −1)/((√((a−1)/(a+1))) +1)) ∣](Q37100.png)
$$\left.\mathrm{1}\right)\:{changemnt}\:{tan}\left(\frac{{t}}{\mathrm{2}}\right)\:={x}\:{give} \\ $$$${f}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{1}}{\mathrm{1}+{a}\:\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }}\:\:\frac{\mathrm{2}{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} \:+{a}\:−{ax}^{\mathrm{2}} }\:=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dx}}{\left(\mathrm{1}−{a}\right){x}^{\mathrm{2}} \:+\mathrm{1}+{a}} \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{1}−{a}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}} \\ $$$${case}\mathrm{1}\:\:\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}>\:{o}\:\Rightarrow\mid{a}\mid<\mathrm{1}\:\:{we}\:{get}\:{by}\:{chang}.{x}=\sqrt{\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}}\:{u} \\ $$$${f}\left({a}\right)\:=\:\frac{\mathrm{2}}{\mathrm{1}−{a}}\:\int_{\mathrm{0}} ^{\sqrt{\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}}} \:\:\:\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:\sqrt{\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}}\:{du} \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{1}−{a}}\:\frac{\sqrt{\mathrm{1}−{a}}}{\sqrt{\mathrm{1}+{a}}}\:\:\left[{arctan}\left({u}\right)\right]_{\mathrm{0}} ^{\sqrt{\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}}} \\ $$$$=\:\frac{\mathrm{2}}{\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\:\:{arctan}\left(\sqrt{\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}}\right) \\ $$$${case}\:\mathrm{2}\:{if}\:\:\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}<\mathrm{0}\:\Rightarrow\:\mid{a}\mid>\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:−\frac{{a}+\mathrm{1}}{{a}−\mathrm{1}}} \\ $$$$=_{{x}\:=\sqrt{\frac{{a}+\mathrm{1}}{{a}−\mathrm{1}}}\:{u}} \:\:\:\:\int_{\mathrm{0}} ^{\sqrt{\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}}} \:\:\:\:\:\frac{\mathrm{1}}{\frac{{a}+\mathrm{1}}{{a}−\mathrm{1}}\left({u}^{\mathrm{2}} −\mathrm{1}\right)}\:\:\sqrt{\frac{{a}+\mathrm{1}}{{a}−\mathrm{1}}}\:{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\frac{\sqrt{{a}−\mathrm{1}}}{\sqrt{{a}+\mathrm{1}}}\:\:\int_{\mathrm{0}} ^{\sqrt{\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}}} \:\:\:\:\left\{\:\frac{\mathrm{1}}{{u}−\mathrm{1}}\:−\frac{\mathrm{1}}{{u}+\mathrm{1}}\right\}{du} \\ $$$$=\:\frac{\sqrt{{a}−\mathrm{1}}}{\mathrm{2}\sqrt{{a}+\mathrm{1}}}\:\left[{ln}\mid\frac{{u}−\mathrm{1}}{{u}+\mathrm{1}}\mid\right]_{\mathrm{0}} ^{\sqrt{\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}}} \\ $$$$=\frac{\sqrt{{a}−\mathrm{1}}}{\mathrm{2}\sqrt{{a}+\mathrm{1}}}\:{ln}\mid\:\:\frac{\sqrt{\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}}\:−\mathrm{1}}{\sqrt{\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}}\:+\mathrm{1}}\mid\:\Rightarrow \\ $$$${f}\left({a}\right)\:=\:\frac{\mathrm{2}}{\mathrm{1}−{a}}\:\frac{\sqrt{{a}−\mathrm{1}}}{\mathrm{2}\sqrt{{a}+\mathrm{1}}}\:{ln}\mid\:\frac{\sqrt{\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}}\:−\mathrm{1}}{\sqrt{\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}}\:+\mathrm{1}}\mid \\ $$$$=\:\frac{−\mathrm{1}}{\sqrt{{a}^{\mathrm{2}} \:−\mathrm{1}}}{ln}\mid\:\frac{\sqrt{\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}}\:−\mathrm{1}}{\sqrt{\frac{{a}−\mathrm{1}}{{a}+\mathrm{1}}}\:+\mathrm{1}}\:\mid \\ $$
Commented by math khazana by abdo last updated on 09/Jun/18
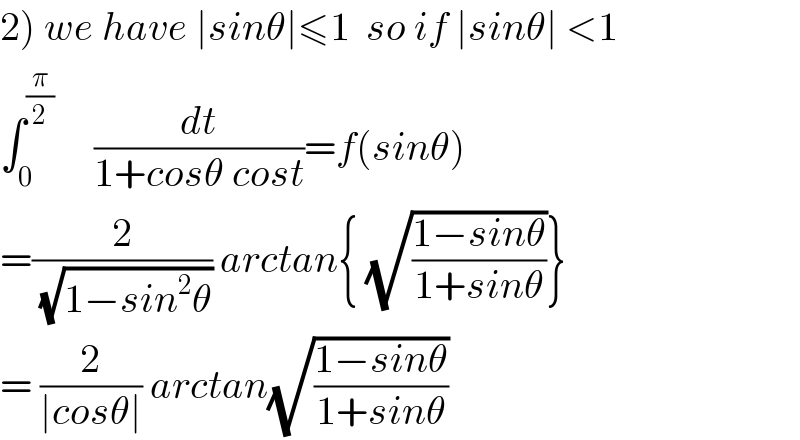
$$\left.\mathrm{2}\right)\:{we}\:{have}\:\mid{sin}\theta\mid\leqslant\mathrm{1}\:\:{so}\:{if}\:\mid{sin}\theta\mid\:<\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\frac{{dt}}{\mathrm{1}+{cos}\theta\:{cost}}={f}\left({sin}\theta\right) \\ $$$$=\frac{\mathrm{2}}{\sqrt{\mathrm{1}−{sin}^{\mathrm{2}} \theta}}\:{arctan}\left\{\:\sqrt{\frac{\mathrm{1}−{sin}\theta}{\mathrm{1}+{sin}\theta}}\right\} \\ $$$$=\:\frac{\mathrm{2}}{\mid{cos}\theta\mid}\:{arctan}\sqrt{\frac{\mathrm{1}−{sin}\theta}{\mathrm{1}+{sin}\theta}} \\ $$
