
Question Number 35225 by abdo mathsup 649 cc last updated on 16/May/18
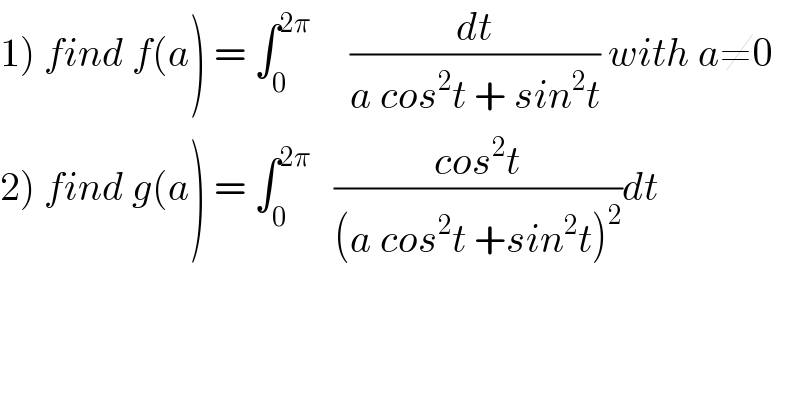
$$\left.\mathrm{1}\right)\:{find}\:{f}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\:\:\frac{{dt}}{{a}\:{cos}^{\mathrm{2}} {t}\:+\:{sin}^{\mathrm{2}} {t}}\:{with}\:{a}\neq\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{g}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{{cos}^{\mathrm{2}} {t}}{\left({a}\:{cos}^{\mathrm{2}} {t}\:+{sin}^{\mathrm{2}} {t}\right)^{\mathrm{2}} }{dt}\: \\ $$
Commented by abdo mathsup 649 cc last updated on 16/May/18

$${a}>\mathrm{0} \\ $$
Commented by prof Abdo imad last updated on 20/May/18
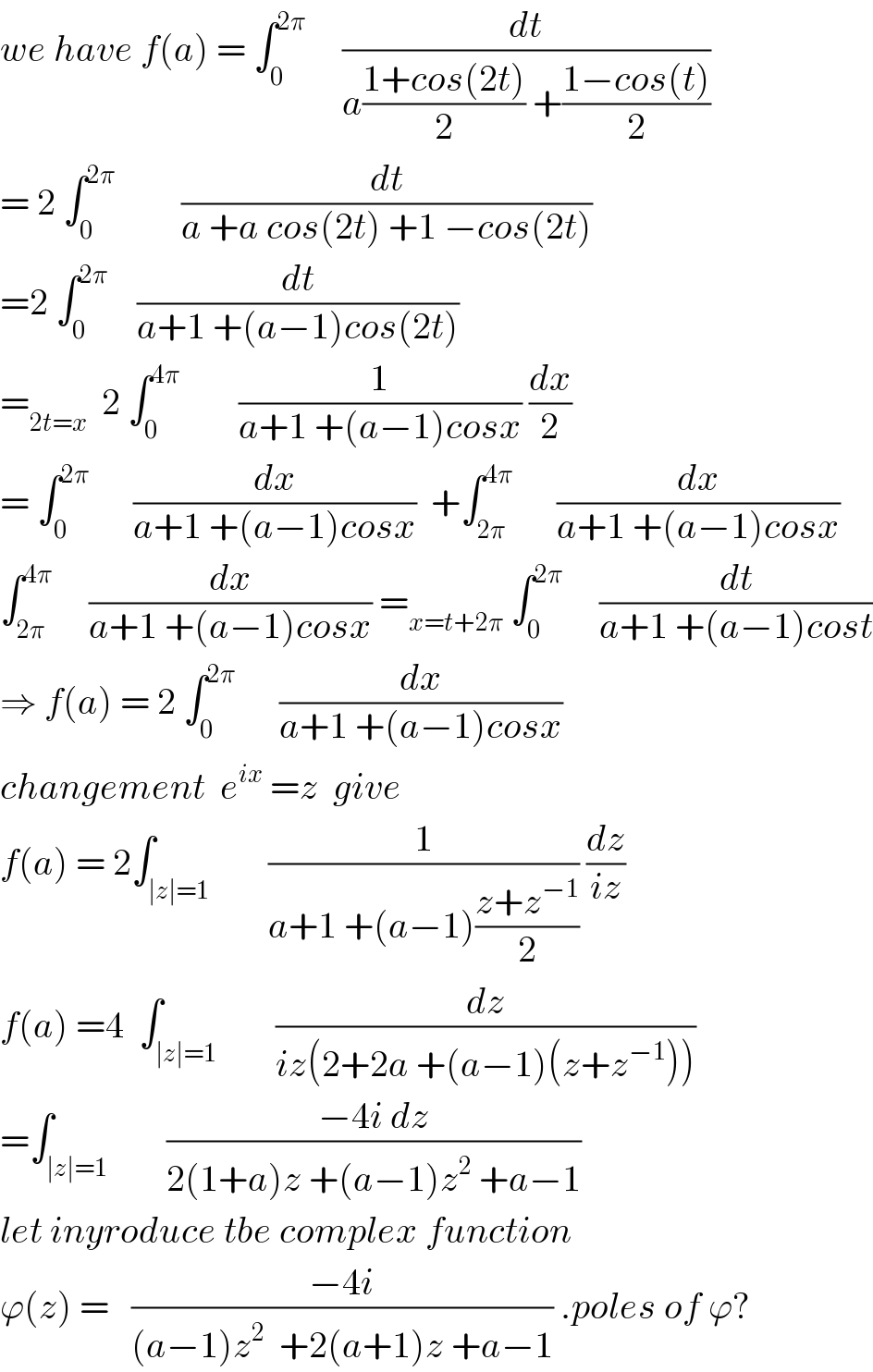
$${we}\:{have}\:{f}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\:\:\frac{{dt}}{{a}\frac{\mathrm{1}+{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\:+\frac{\mathrm{1}−{cos}\left({t}\right)}{\mathrm{2}}} \\ $$$$=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\:\:\:\:\:\:\frac{{dt}}{{a}\:+{a}\:{cos}\left(\mathrm{2}{t}\right)\:+\mathrm{1}\:−{cos}\left(\mathrm{2}{t}\right)} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\:\frac{{dt}}{{a}+\mathrm{1}\:+\left({a}−\mathrm{1}\right){cos}\left(\mathrm{2}{t}\right)} \\ $$$$=_{\mathrm{2}{t}={x}} \:\:\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{4}\pi} \:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{a}+\mathrm{1}\:+\left({a}−\mathrm{1}\right){cosx}}\:\frac{{dx}}{\mathrm{2}} \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\:\:\:\frac{{dx}}{{a}+\mathrm{1}\:+\left({a}−\mathrm{1}\right){cosx}}\:\:+\int_{\mathrm{2}\pi} ^{\mathrm{4}\pi} \:\:\:\:\:\:\frac{{dx}}{{a}+\mathrm{1}\:+\left({a}−\mathrm{1}\right){cosx}} \\ $$$$\int_{\mathrm{2}\pi} ^{\mathrm{4}\pi} \:\:\:\:\:\frac{{dx}}{{a}+\mathrm{1}\:+\left({a}−\mathrm{1}\right){cosx}}\:=_{{x}={t}+\mathrm{2}\pi} \:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\:\:\frac{{dt}}{{a}+\mathrm{1}\:+\left({a}−\mathrm{1}\right){cost}} \\ $$$$\Rightarrow\:{f}\left({a}\right)\:=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\:\:\:\frac{{dx}}{{a}+\mathrm{1}\:+\left({a}−\mathrm{1}\right){cosx}} \\ $$$${changement}\:\:{e}^{{ix}} \:={z}\:\:{give} \\ $$$${f}\left({a}\right)\:=\:\mathrm{2}\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\:\:\frac{\mathrm{1}}{{a}+\mathrm{1}\:+\left({a}−\mathrm{1}\right)\frac{{z}+{z}^{−\mathrm{1}} }{\mathrm{2}}}\:\frac{{dz}}{{iz}} \\ $$$${f}\left({a}\right)\:=\mathrm{4}\:\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\:\:\frac{{dz}}{{iz}\left(\mathrm{2}+\mathrm{2}{a}\:+\left({a}−\mathrm{1}\right)\left({z}+{z}^{−\mathrm{1}} \right)\right)} \\ $$$$=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\:\:\frac{−\mathrm{4}{i}\:{dz}}{\mathrm{2}\left(\mathrm{1}+{a}\right){z}\:+\left({a}−\mathrm{1}\right){z}^{\mathrm{2}} \:+{a}−\mathrm{1}} \\ $$$${let}\:{inyroduce}\:{tbe}\:{complex}\:{function} \\ $$$$\varphi\left({z}\right)\:=\:\:\:\frac{−\mathrm{4}{i}}{\left({a}−\mathrm{1}\right){z}^{\mathrm{2}} \:\:+\mathrm{2}\left({a}+\mathrm{1}\right){z}\:+{a}−\mathrm{1}}\:.{poles}\:{of}\:\varphi? \\ $$
Commented by abdo mathsup 649 cc last updated on 20/May/18
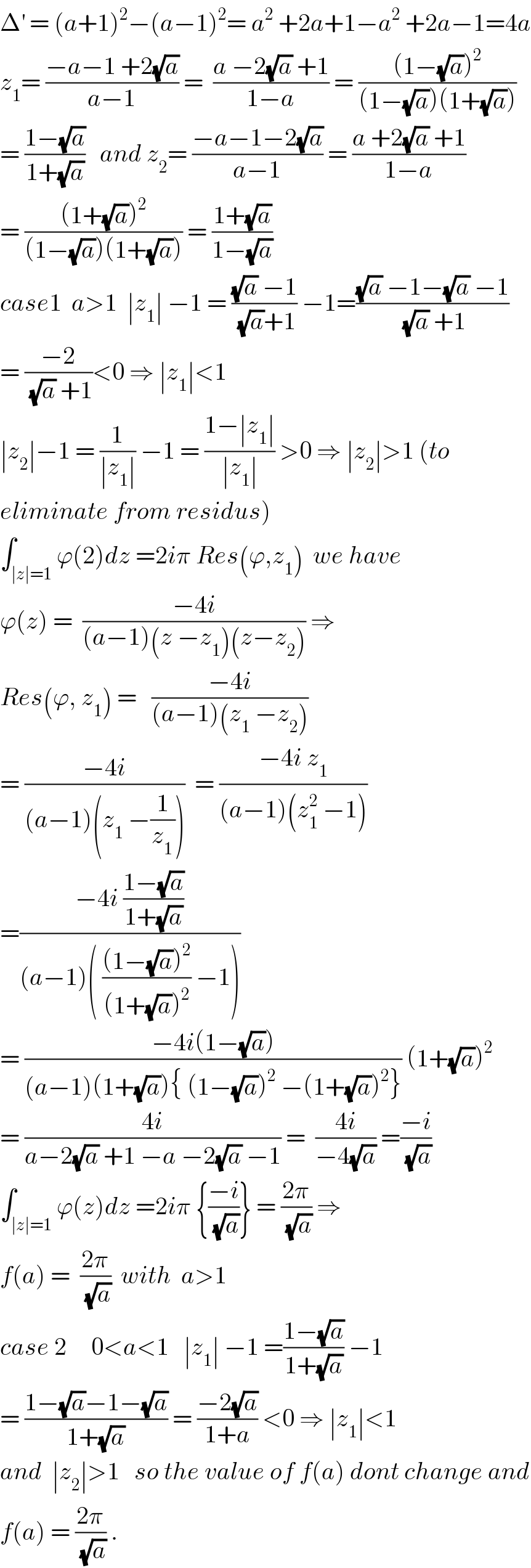
$$\Delta^{'} \:=\:\left({a}+\mathrm{1}\right)^{\mathrm{2}} −\left({a}−\mathrm{1}\right)^{\mathrm{2}} =\:{a}^{\mathrm{2}} \:+\mathrm{2}{a}+\mathrm{1}−{a}^{\mathrm{2}} \:+\mathrm{2}{a}−\mathrm{1}=\mathrm{4}{a} \\ $$$${z}_{\mathrm{1}} =\:\frac{−{a}−\mathrm{1}\:+\mathrm{2}\sqrt{{a}}}{{a}−\mathrm{1}}\:=\:\:\frac{{a}\:−\mathrm{2}\sqrt{{a}}\:+\mathrm{1}}{\mathrm{1}−{a}}\:=\:\frac{\left(\mathrm{1}−\sqrt{{a}}\right)^{\mathrm{2}} }{\left(\mathrm{1}−\sqrt{{a}}\right)\left(\mathrm{1}+\sqrt{{a}}\right)} \\ $$$$=\:\frac{\mathrm{1}−\sqrt{{a}}}{\mathrm{1}+\sqrt{{a}}}\:\:\:{and}\:{z}_{\mathrm{2}} =\:\frac{−{a}−\mathrm{1}−\mathrm{2}\sqrt{{a}}}{{a}−\mathrm{1}}\:=\:\frac{{a}\:+\mathrm{2}\sqrt{{a}}\:+\mathrm{1}}{\mathrm{1}−{a}} \\ $$$$=\:\frac{\left(\mathrm{1}+\sqrt{{a}}\right)^{\mathrm{2}} }{\left(\mathrm{1}−\sqrt{{a}}\right)\left(\mathrm{1}+\sqrt{{a}}\right)}\:=\:\frac{\mathrm{1}+\sqrt{{a}}}{\mathrm{1}−\sqrt{{a}}} \\ $$$${case}\mathrm{1}\:\:{a}>\mathrm{1}\:\:\mid{z}_{\mathrm{1}} \mid\:−\mathrm{1}\:=\:\frac{\sqrt{{a}}\:−\mathrm{1}}{\sqrt{{a}}+\mathrm{1}}\:−\mathrm{1}=\frac{\sqrt{{a}}\:−\mathrm{1}−\sqrt{{a}}\:−\mathrm{1}}{\sqrt{{a}}\:+\mathrm{1}} \\ $$$$=\:\frac{−\mathrm{2}}{\sqrt{{a}}\:+\mathrm{1}}<\mathrm{0}\:\Rightarrow\:\mid{z}_{\mathrm{1}} \mid<\mathrm{1} \\ $$$$\mid{z}_{\mathrm{2}} \mid−\mathrm{1}\:=\:\frac{\mathrm{1}}{\mid{z}_{\mathrm{1}} \mid}\:−\mathrm{1}\:=\:\frac{\mathrm{1}−\mid{z}_{\mathrm{1}} \mid}{\mid{z}_{\mathrm{1}} \mid}\:>\mathrm{0}\:\Rightarrow\:\mid{z}_{\mathrm{2}} \mid>\mathrm{1}\:\left({to}\right. \\ $$$$\left.{eliminate}\:{from}\:{residus}\right) \\ $$$$\int_{\mid{z}\mid=\mathrm{1}} \varphi\left(\mathrm{2}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{z}_{\mathrm{1}} \right)\:\:{we}\:{have} \\ $$$$\varphi\left({z}\right)\:=\:\:\frac{−\mathrm{4}{i}}{\left({a}−\mathrm{1}\right)\left({z}\:−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)}\:\Rightarrow \\ $$$${Res}\left(\varphi,\:{z}_{\mathrm{1}} \right)\:=\:\:\:\frac{−\mathrm{4}{i}}{\left({a}−\mathrm{1}\right)\left({z}_{\mathrm{1}} \:−{z}_{\mathrm{2}} \right)} \\ $$$$=\:\frac{−\mathrm{4}{i}}{\left({a}−\mathrm{1}\right)\left({z}_{\mathrm{1}} \:−\frac{\mathrm{1}}{{z}_{\mathrm{1}} }\right)}\:\:=\:\frac{−\mathrm{4}{i}\:{z}_{\mathrm{1}} }{\left({a}−\mathrm{1}\right)\left({z}_{\mathrm{1}} ^{\mathrm{2}} \:−\mathrm{1}\right)} \\ $$$$=\frac{−\mathrm{4}{i}\:\frac{\mathrm{1}−\sqrt{{a}}}{\mathrm{1}+\sqrt{{a}}}}{\left({a}−\mathrm{1}\right)\left(\:\frac{\left(\mathrm{1}−\sqrt{{a}}\right)^{\mathrm{2}} }{\left(\mathrm{1}+\sqrt{{a}}\right)^{\mathrm{2}} }\:−\mathrm{1}\right)} \\ $$$$=\:\frac{−\mathrm{4}{i}\left(\mathrm{1}−\sqrt{{a}}\right)}{\left({a}−\mathrm{1}\right)\left(\mathrm{1}+\sqrt{{a}}\right)\left\{\:\left(\mathrm{1}−\sqrt{{a}}\right)^{\mathrm{2}} \:−\left(\mathrm{1}+\sqrt{{a}}\right)^{\mathrm{2}} \right\}}\:\left(\mathrm{1}+\sqrt{{a}}\right)^{\mathrm{2}} \\ $$$$=\:\frac{\mathrm{4}{i}}{{a}−\mathrm{2}\sqrt{{a}}\:+\mathrm{1}\:−{a}\:−\mathrm{2}\sqrt{{a}}\:−\mathrm{1}}\:=\:\:\frac{\mathrm{4}{i}}{−\mathrm{4}\sqrt{{a}}}\:=\frac{−{i}}{\sqrt{{a}}} \\ $$$$\int_{\mid{z}\mid=\mathrm{1}} \varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\left\{\frac{−{i}}{\sqrt{{a}}}\right\}\:=\:\frac{\mathrm{2}\pi}{\sqrt{{a}}}\:\Rightarrow\: \\ $$$${f}\left({a}\right)\:=\:\:\frac{\mathrm{2}\pi}{\sqrt{{a}}}\:\:{with}\:\:{a}>\mathrm{1} \\ $$$${case}\:\mathrm{2}\:\:\:\:\:\mathrm{0}<{a}<\mathrm{1}\:\:\:\mid{z}_{\mathrm{1}} \mid\:−\mathrm{1}\:=\frac{\mathrm{1}−\sqrt{{a}}}{\mathrm{1}+\sqrt{{a}}}\:−\mathrm{1} \\ $$$$=\:\frac{\mathrm{1}−\sqrt{{a}}−\mathrm{1}−\sqrt{{a}}}{\mathrm{1}+\sqrt{{a}}}\:=\:\frac{−\mathrm{2}\sqrt{{a}}}{\mathrm{1}+{a}}\:<\mathrm{0}\:\Rightarrow\:\mid{z}_{\mathrm{1}} \mid<\mathrm{1} \\ $$$${and}\:\:\mid{z}_{\mathrm{2}} \mid>\mathrm{1}\:\:\:{so}\:{the}\:{value}\:{of}\:{f}\left({a}\right)\:{dont}\:{change}\:{and} \\ $$$${f}\left({a}\right)\:=\:\frac{\mathrm{2}\pi}{\sqrt{{a}}}\:. \\ $$
Commented by abdo mathsup 649 cc last updated on 20/May/18
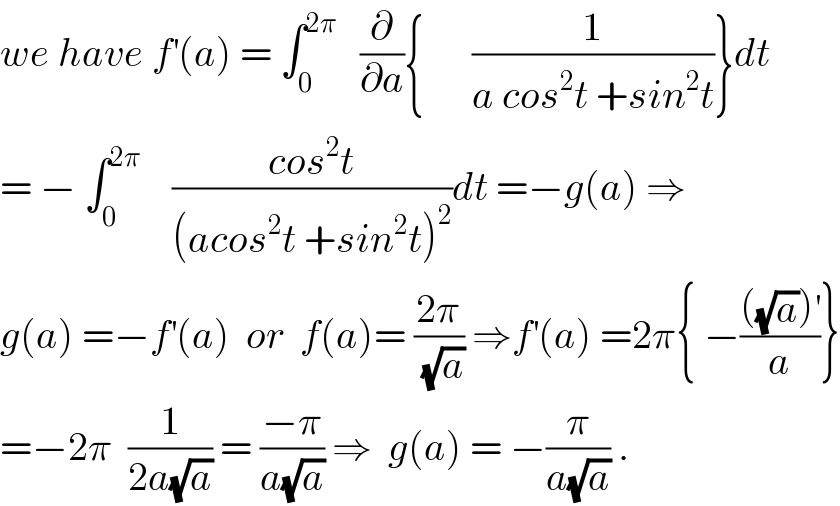
$${we}\:{have}\:{f}^{'} \left({a}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{\partial}{\partial{a}}\left\{\:\:\:\:\:\:\frac{\mathrm{1}}{{a}\:{cos}^{\mathrm{2}} {t}\:+{sin}^{\mathrm{2}} {t}}\right\}{dt} \\ $$$$=\:−\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\:\frac{{cos}^{\mathrm{2}} {t}}{\left({acos}^{\mathrm{2}} {t}\:+{sin}^{\mathrm{2}} {t}\right)^{\mathrm{2}} }{dt}\:=−{g}\left({a}\right)\:\Rightarrow \\ $$$${g}\left({a}\right)\:=−{f}^{'} \left({a}\right)\:\:{or}\:\:{f}\left({a}\right)=\:\frac{\mathrm{2}\pi}{\sqrt{{a}}}\:\Rightarrow{f}^{'} \left({a}\right)\:=\mathrm{2}\pi\left\{\:−\frac{\left(\sqrt{{a}}\right)^{'} }{{a}}\right\} \\ $$$$=−\mathrm{2}\pi\:\:\frac{\mathrm{1}}{\mathrm{2}{a}\sqrt{{a}}}\:=\:\frac{−\pi}{{a}\sqrt{{a}}}\:\Rightarrow\:\:{g}\left({a}\right)\:=\:−\frac{\pi}{{a}\sqrt{{a}}}\:. \\ $$
