
Question Number 53228 by maxmathsup by imad last updated on 19/Jan/19
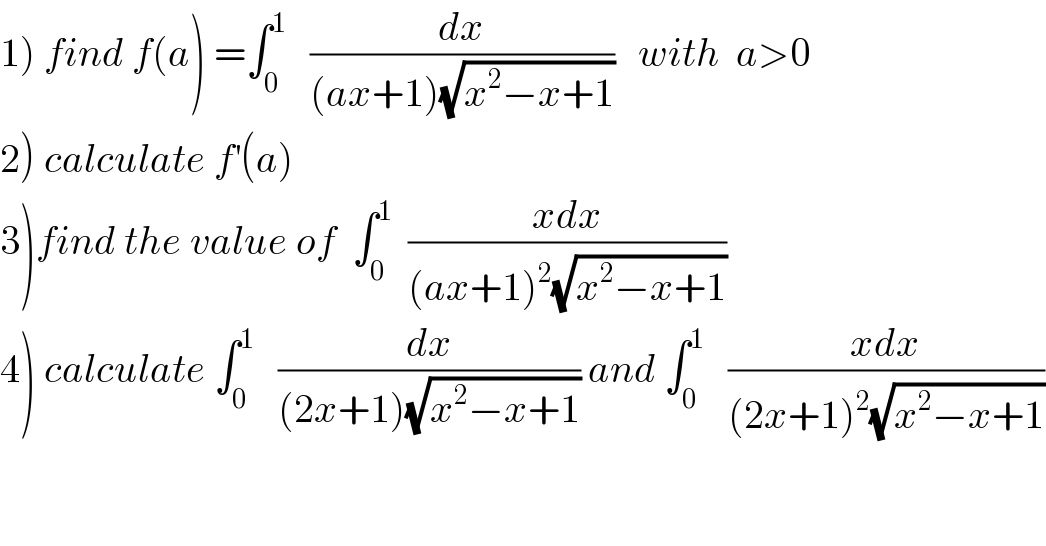
$$\left.\mathrm{1}\right)\:{find}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dx}}{\left({ax}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}\:\:\:{with}\:\:{a}>\mathrm{0} \\ $$ $$\left.\mathrm{2}\right)\:{calculate}\:{f}^{'} \left({a}\right) \\ $$ $$\left.\mathrm{3}\right){find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{xdx}}{\left({ax}+\mathrm{1}\right)^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}} \\ $$ $$\left.\mathrm{4}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dx}}{\left(\mathrm{2}{x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}\:{and}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{xdx}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}} \\ $$
Commented byAbdo msup. last updated on 20/Jan/19
![1)we have x^2 −x +1 =(x−(1/2))^2 +(3/4) changement x−(1/2) =((√3)/2)sh(t) give f(a) = ∫_(argsh(−(1/(√3)))) ^(argsh((1/(√3)))) (1/((a((1/2)+((√3)/2)sh(t))+1)((√3)/2)ch(t)))((√3)/2)ch(t)dt =∫_(ln(−(1/(√3)) +(2/(√3)))) ^(ln((1/(√3)) +(2/(√3)))) ((2dt)/(a +a(√3)sh(t)+2)) =∫_(ln((1/(√3)))) ^(ln((√3))) ((2dt)/(a+a(√3)((e^t −e^(−t) )/2)+2)) = 4 ∫_(ln((1/(√3)))) ^(ln((√3))) (dt/(2a +a(√3)(e^t −e^(−t) )+4)) =_(e^t =u) 4 ∫_(1/(√3)) ^(√3) (1/(2a+a(√3)(u−u^(−1) )+4)) (du/u) =4 ∫_(1/(√3)) ^(√3) (du/(2au +a(√3)u^2 −a(√3) +4u)) =4 ∫_(1/(√3)) ^(√3) (du/(a(√3)u^2 +(2a+4)u−a(√3))) roots of p(u)=a(√3)u^2 +(2a+4)u−a(√3) Δ^′ =(a+2)^2 +3a^2 =a^2 +4a +4 +3a^2 =4a^2 +4a + u_1 =((−a−2+2(√(1+a+a^2 )))/(a(√3))) u_2 =((−a−2−2(√(1+a+a^2 )))/(a(√3))) ⇒ F(u) =(1/(a(√3)(u−u_1 )(u−u_2 ))) =(1/(a(√3)))(1/(u_1 −u_2 )){ (1/(u−u_1 )) −(1/(u−u_2 ))} =(1/(a(√3))) (1/((4(√(1+a+a^2 )))/(a(√3)))) {(1/(u−u_1 )) −(1/(u−u_2 ))} =(1/(4(√(1+a+a^2 )))){(1/(u−u_1 )) −(1/(u−u_2 ))}? ⇒ f(a) =(1/(√(1+a+a^2 ))) [ln∣((u−u_1 )/(u−u_2 ))∣]_(1/(√3)) ^(√3) =(1/(√(1+a+a^2 ))){ln∣(((√3)−u_1 )/((√3)−u_2 ))∣−ln∣(((1/(√3))−u_1 )/((1/(√3))−u_2 ))∣} =(1/(√(1+a+a^2 ))){ln∣(((√3)−((−a−2+2(√(1+a+a^2 )))/(a(√3))))/((√3)−((−a−2+2(√(1+a+a^2 )))/(a(√3)))))∣ −ln∣((1−(√3)((−a−2+2(√(1+a+a^2 )))/(a(√3))))/(1−(√3)((−a−2 −2(√(1+a+a^2 )))/(a(√3)))))∣ =(1/(√(1+a+a^2 ))){ ln∣((4a+2+2(√(1+a+a^2 )))/(4a+2−2(√(1+a+a^2 ))))∣ −ln∣ ((2a(√3)+2−2(√(1+a+a^2 )))/(2a(√3)+2 +2(√(1+a+a^2 ))))∣} ⇒f(a) =(1/(√(1+a+a^2 ))){ ln∣((2a+1+(√(1+a+a^2 )))/(2a+1−(√(1+a+a^2 ))))∣ −ln∣((a(√3)+1−(√(1+a+a^2 )))/(a(√3)+1 +(√(1+a+a^2 ))))∣} .](Q53320.png)
$$\left.\mathrm{1}\right){we}\:{have}\:{x}^{\mathrm{2}} −{x}\:+\mathrm{1}\:=\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\:{changement} \\ $$ $${x}−\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)\:{give}\: \\ $$ $${f}\left({a}\right)\:=\:\int_{{argsh}\left(−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)} ^{{argsh}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)} \:\:\:\:\frac{\mathrm{1}}{\left({a}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)\right)+\mathrm{1}\right)\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{ch}\left({t}\right)}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{ch}\left({t}\right){dt} \\ $$ $$=\int_{{ln}\left(−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:+\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\right)} ^{{ln}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:+\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\right)} \:\:\:\frac{\mathrm{2}{dt}}{{a}\:+{a}\sqrt{\mathrm{3}}{sh}\left({t}\right)+\mathrm{2}} \\ $$ $$=\int_{{ln}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)} ^{{ln}\left(\sqrt{\mathrm{3}}\right)} \:\:\:\frac{\mathrm{2}{dt}}{{a}+{a}\sqrt{\mathrm{3}}\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}}+\mathrm{2}} \\ $$ $$=\:\mathrm{4}\:\int_{{ln}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)} ^{{ln}\left(\sqrt{\mathrm{3}}\right)} \:\:\:\:\frac{{dt}}{\mathrm{2}{a}\:+{a}\sqrt{\mathrm{3}}\left({e}^{{t}} −{e}^{−{t}} \right)+\mathrm{4}} \\ $$ $$=_{{e}^{{t}} ={u}} \:\:\:\:\mathrm{4}\:\int_{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\sqrt{\mathrm{3}}} \:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}{a}+{a}\sqrt{\mathrm{3}}\left({u}−{u}^{−\mathrm{1}} \right)+\mathrm{4}}\:\frac{{du}}{{u}} \\ $$ $$=\mathrm{4}\:\int_{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\sqrt{\mathrm{3}}} \:\:\:\:\:\:\:\frac{{du}}{\mathrm{2}{au}\:+{a}\sqrt{\mathrm{3}}{u}^{\mathrm{2}} \:−{a}\sqrt{\mathrm{3}}\:+\mathrm{4}{u}} \\ $$ $$=\mathrm{4}\:\int_{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\sqrt{\mathrm{3}}} \:\:\:\frac{{du}}{{a}\sqrt{\mathrm{3}}{u}^{\mathrm{2}} \:+\left(\mathrm{2}{a}+\mathrm{4}\right){u}−{a}\sqrt{\mathrm{3}}} \\ $$ $${roots}\:{of}\:{p}\left({u}\right)={a}\sqrt{\mathrm{3}}{u}^{\mathrm{2}} +\left(\mathrm{2}{a}+\mathrm{4}\right){u}−{a}\sqrt{\mathrm{3}} \\ $$ $$\Delta^{'} =\left({a}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} \:={a}^{\mathrm{2}} +\mathrm{4}{a}\:+\mathrm{4}\:+\mathrm{3}{a}^{\mathrm{2}} =\mathrm{4}{a}^{\mathrm{2}} +\mathrm{4}{a}\:+ \\ $$ $${u}_{\mathrm{1}} =\frac{−{a}−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}{{a}\sqrt{\mathrm{3}}} \\ $$ $${u}_{\mathrm{2}} =\frac{−{a}−\mathrm{2}−\mathrm{2}\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}{{a}\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$ $${F}\left({u}\right)\:=\frac{\mathrm{1}}{{a}\sqrt{\mathrm{3}}\left({u}−{u}_{\mathrm{1}} \right)\left({u}−{u}_{\mathrm{2}} \right)} \\ $$ $$=\frac{\mathrm{1}}{{a}\sqrt{\mathrm{3}}}\frac{\mathrm{1}}{{u}_{\mathrm{1}} −{u}_{\mathrm{2}} }\left\{\:\frac{\mathrm{1}}{{u}−{u}_{\mathrm{1}} }\:−\frac{\mathrm{1}}{{u}−{u}_{\mathrm{2}} }\right\} \\ $$ $$=\frac{\mathrm{1}}{{a}\sqrt{\mathrm{3}}}\:\frac{\mathrm{1}}{\frac{\mathrm{4}\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}{{a}\sqrt{\mathrm{3}}}}\:\left\{\frac{\mathrm{1}}{{u}−{u}_{\mathrm{1}} }\:−\frac{\mathrm{1}}{{u}−{u}_{\mathrm{2}} }\right\} \\ $$ $$=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}\left\{\frac{\mathrm{1}}{{u}−{u}_{\mathrm{1}} }\:−\frac{\mathrm{1}}{{u}−{u}_{\mathrm{2}} }\right\}?\:\Rightarrow \\ $$ $${f}\left({a}\right)\:=\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}\:\left[{ln}\mid\frac{{u}−{u}_{\mathrm{1}} }{{u}−{u}_{\mathrm{2}} }\mid\right]_{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\sqrt{\mathrm{3}}} \\ $$ $$=\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}\left\{{ln}\mid\frac{\sqrt{\mathrm{3}}−{u}_{\mathrm{1}} }{\sqrt{\mathrm{3}}−{u}_{\mathrm{2}} }\mid−{ln}\mid\frac{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}−{u}_{\mathrm{1}} }{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}−{u}_{\mathrm{2}} }\mid\right\} \\ $$ $$=\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}\left\{{ln}\mid\frac{\sqrt{\mathrm{3}}−\frac{−{a}−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}{{a}\sqrt{\mathrm{3}}}}{\sqrt{\mathrm{3}}−\frac{−{a}−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}{{a}\sqrt{\mathrm{3}}}}\mid\right. \\ $$ $$−{ln}\mid\frac{\mathrm{1}−\sqrt{\mathrm{3}}\frac{−{a}−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}{{a}\sqrt{\mathrm{3}}}}{\mathrm{1}−\sqrt{\mathrm{3}}\frac{−{a}−\mathrm{2}\:−\mathrm{2}\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}{{a}\sqrt{\mathrm{3}}}}\mid \\ $$ $$=\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}\left\{\:{ln}\mid\frac{\mathrm{4}{a}+\mathrm{2}+\mathrm{2}\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}{\mathrm{4}{a}+\mathrm{2}−\mathrm{2}\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}\mid\right. \\ $$ $$\left.−{ln}\mid\:\frac{\mathrm{2}{a}\sqrt{\mathrm{3}}+\mathrm{2}−\mathrm{2}\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}{\mathrm{2}{a}\sqrt{\mathrm{3}}+\mathrm{2}\:+\mathrm{2}\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}\mid\right\} \\ $$ $$\Rightarrow{f}\left({a}\right)\:=\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}\left\{\:{ln}\mid\frac{\mathrm{2}{a}+\mathrm{1}+\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}{\mathrm{2}{a}+\mathrm{1}−\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}\mid\right. \\ $$ $$\left.−{ln}\mid\frac{{a}\sqrt{\mathrm{3}}+\mathrm{1}−\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}{{a}\sqrt{\mathrm{3}}+\mathrm{1}\:+\sqrt{\mathrm{1}+{a}+{a}^{\mathrm{2}} }}\mid\right\}\:. \\ $$ $$ \\ $$
Commented byAbdo msup. last updated on 20/Jan/19
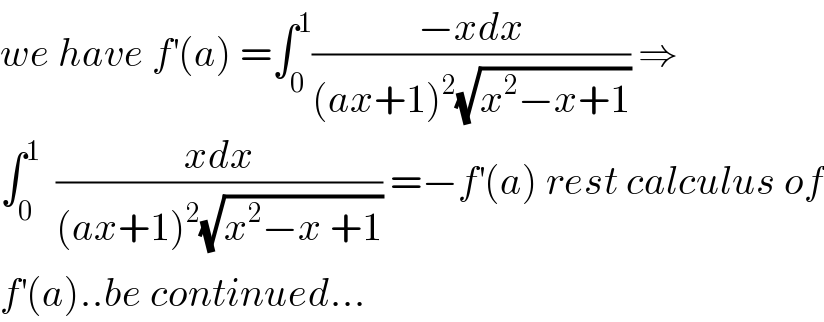
$${we}\:{have}\:{f}^{'} \left({a}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−{xdx}}{\left({ax}+\mathrm{1}\right)^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}\:\Rightarrow \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{xdx}}{\left({ax}+\mathrm{1}\right)^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}}}\:=−{f}^{'} \left({a}\right)\:{rest}\:{calculus}\:{of} \\ $$ $${f}^{'} \left({a}\right)..{be}\:{continued}... \\ $$
Commented byAbdo msup. last updated on 20/Jan/19
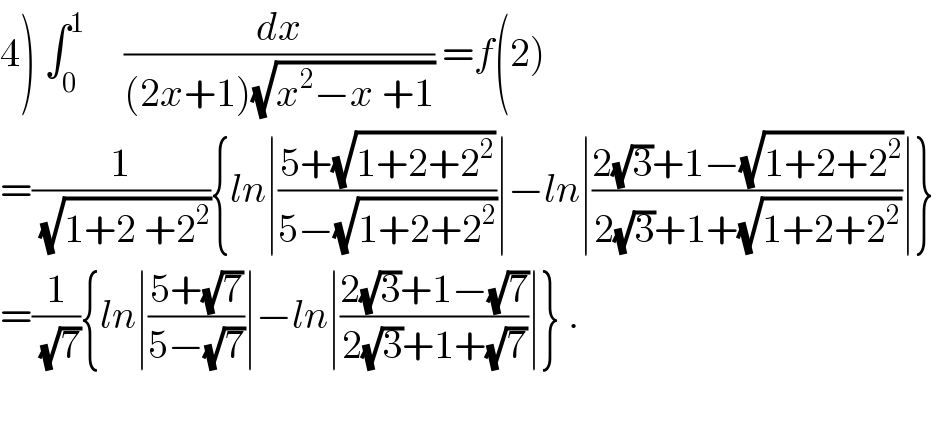
$$\left.\mathrm{4}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\frac{{dx}}{\left(\mathrm{2}{x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}}}\:={f}\left(\mathrm{2}\right) \\ $$ $$=\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\mathrm{2}\:+\mathrm{2}^{\mathrm{2}} }}\left\{{ln}\mid\frac{\mathrm{5}+\sqrt{\mathrm{1}+\mathrm{2}+\mathrm{2}^{\mathrm{2}} }}{\mathrm{5}−\sqrt{\mathrm{1}+\mathrm{2}+\mathrm{2}^{\mathrm{2}} }}\mid−{ln}\mid\frac{\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{2}+\mathrm{2}^{\mathrm{2}} }}{\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{2}+\mathrm{2}^{\mathrm{2}} }}\mid\right\} \\ $$ $$=\frac{\mathrm{1}}{\sqrt{\mathrm{7}}}\left\{{ln}\mid\frac{\mathrm{5}+\sqrt{\mathrm{7}}}{\mathrm{5}−\sqrt{\mathrm{7}}}\mid−{ln}\mid\frac{\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{1}−\sqrt{\mathrm{7}}}{\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{1}+\sqrt{\mathrm{7}}}\mid\right\}\:. \\ $$ $$ \\ $$
