Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 62811 by mathmax by abdo last updated on 25/Jun/19

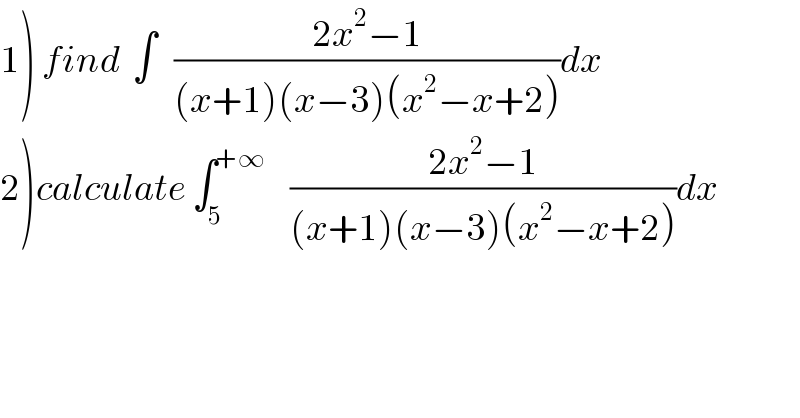
1) find ∫ ((2x^2 −1)/((x+1)(x−3)(x^2 −x+2)))dx 2)calculate ∫_5 ^(+∞) ((2x^2 −1)/((x+1)(x−3)(x^2 −x+2)))dx

$$\left.\mathrm{1}\right)\:{find}\:\:\int\:\:\:\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{3}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)}{dx} \\ $$$$\left.\mathrm{2}\right){calculate}\:\int_{\mathrm{5}} ^{+\infty} \:\:\:\:\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{3}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)}{dx} \\ $$

Commented by Prithwish sen last updated on 25/Jun/19

1)((2x^2 −1)/((x+1)(x−3)(x^2 −x+2))) =(A/(x+1)) + (B/(x−3)) +((Cx+D)/(x^2 −x+2)) By calculating we get ∫[((−1)/(16(x+1))) +((17)/(32(x−3))) −((15(2x−1))/(32(x^2 −x+2))) −(1/(16(x^2 −x+2))) ] dx = −(1/(16)) ln(x+1)+((17)/(32)) ln(x−3) −((15)/(32)) ln(x^2 −x+2)−(1/(8(√7))) tan^(−1) ((2x−1)/(√7)) +C waiting for feedbacks

$$\left.\mathrm{1}\right)\frac{\mathrm{2x}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{3}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{2}\right)}\:\:=\frac{\mathrm{A}}{\mathrm{x}+\mathrm{1}}\:+\:\frac{\mathrm{B}}{\mathrm{x}−\mathrm{3}}\:+\frac{\mathrm{Cx}+\mathrm{D}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{2}} \\ $$$$\mathrm{By}\:\mathrm{calculating}\:\mathrm{we}\:\mathrm{get} \\ $$$$\int\left[\frac{−\mathrm{1}}{\mathrm{16}\left(\mathrm{x}+\mathrm{1}\right)}\:+\frac{\mathrm{17}}{\mathrm{32}\left(\mathrm{x}−\mathrm{3}\right)}\:−\frac{\mathrm{15}\left(\mathrm{2x}−\mathrm{1}\right)}{\mathrm{32}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{2}\right)}\:−\frac{\mathrm{1}}{\mathrm{16}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{2}\right)}\:\right]\:\mathrm{dx} \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{16}}\:\mathrm{ln}\left(\mathrm{x}+\mathrm{1}\right)+\frac{\mathrm{17}}{\mathrm{32}}\:\mathrm{ln}\left(\mathrm{x}−\mathrm{3}\right)\:−\frac{\mathrm{15}}{\mathrm{32}}\:\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{7}}}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2x}−\mathrm{1}}{\sqrt{\mathrm{7}}}\:+\mathrm{C} \\ $$$$\mathrm{waiting}\:\mathrm{for}\:\mathrm{feedbacks} \\ $$

Commented by mathmax by abdo last updated on 26/Jun/19

1)let decompose F(x)=((2x^2 −1)/((x+1)(x−3)(x^2 −x+2))) F(x)=(a/(x+1)) +(b/(x−3)) +((cx+d)/(x^2 −x+2)) a=lim_(x→−1) (x+1)F(x)=(1/((−4)(4))) =−(1/(16)) b=lim_(x→3) (x−3)F(x) =((17)/(4(8))) =((17)/(32)) ⇒F(x)=((−1)/(16(x+1))) +((17)/(32(x−3))) +((cx+d)/(x^2 −x+2)) lim_(x→+∞) xF(x)=0 =−(1/(16))+((17)/(32)) +c =((15)/(32)) +c ⇒c =−((15)/(32)) ⇒ F(x)=((−1)/(16(x+1))) +((17)/(32(x−3))) +((−((15)/(32))x+d)/(x^2 −x+2)) F(0)=((−1)/(−6)) =(1/6) =−(1/(16)) −((17)/(3.32)) +(d/2) ⇒(1/3) =−(1/8) −((17)/(48)) +d ⇒d =(1/3) +(1/8) +((17)/(48)) =((11)/(24)) +((17)/(48)) =((22+17)/(48)) =((39)/(48)) ⇒ ∫ ((2x^2 −1)/((x+1)(x−3)(x^2 −x+2)))dx =−(1/(16))∫(dx/(x+1)) +((17)/(32))∫ (dx/(x−3)) −((15)/(32))∫ (x/(x^2 −x+2))dx +((39)/(48)) ∫ (dx/(x^2 −x+2)) +c =−(1/(16))ln∣x+1∣+((17)/(32))ln∣x−3∣−((15)/(64)) ∫ ((2x−1+1)/(x^2 −x+2))dx +((39)/(48)) ∫ (dx/(x^2 −x+2)) +c =−(1/(16))ln∣x+1∣+((17)/(32))ln∣x−3∣−((15)/(64))ln(x^2 −x+2)+(((39)/(48))−((15)/(64)))∫ (dx/(x^2 −x+2))dx +c but ∫ (dx/(x^2 −x+2)) =∫ (dx/(x^2 −x+(1/4)+2−(1/4))) =∫ (dx/((x−(1/2))^2 +(7/4))) =_(x−(1/2)=((√7)/2)u) (4/7) ∫ (1/(1+u^2 ))((√7)/2)du =(2/(√7)) arctan(((2x−1)/(√7))) ⇒ ∫ F(x)dx =−(1/(16))ln∣x+1∣+((17)/(32))ln∣x−3∣−((15)/(64))ln(x^2 −x+2)+(((39)/(48))−((15)/(64)))(2/(√7)) arctan(((2x−1)/(√7))) +c

$$\left.\mathrm{1}\right){let}\:{decompose}\:{F}\left({x}\right)=\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{3}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)} \\ $$$${F}\left({x}\right)=\frac{{a}}{{x}+\mathrm{1}}\:+\frac{{b}}{{x}−\mathrm{3}}\:+\frac{{cx}+{d}}{{x}^{\mathrm{2}} −{x}+\mathrm{2}} \\ $$$${a}={lim}_{{x}\rightarrow−\mathrm{1}} \left({x}+\mathrm{1}\right){F}\left({x}\right)=\frac{\mathrm{1}}{\left(−\mathrm{4}\right)\left(\mathrm{4}\right)}\:=−\frac{\mathrm{1}}{\mathrm{16}} \\ $$$${b}={lim}_{{x}\rightarrow\mathrm{3}} \left({x}−\mathrm{3}\right){F}\left({x}\right)\:=\frac{\mathrm{17}}{\mathrm{4}\left(\mathrm{8}\right)}\:=\frac{\mathrm{17}}{\mathrm{32}}\:\Rightarrow{F}\left({x}\right)=\frac{−\mathrm{1}}{\mathrm{16}\left({x}+\mathrm{1}\right)}\:+\frac{\mathrm{17}}{\mathrm{32}\left({x}−\mathrm{3}\right)}\:+\frac{{cx}+{d}}{{x}^{\mathrm{2}} −{x}+\mathrm{2}} \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)=\mathrm{0}\:=−\frac{\mathrm{1}}{\mathrm{16}}+\frac{\mathrm{17}}{\mathrm{32}}\:+{c}\:=\frac{\mathrm{15}}{\mathrm{32}}\:+{c}\:\Rightarrow{c}\:=−\frac{\mathrm{15}}{\mathrm{32}}\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{−\mathrm{1}}{\mathrm{16}\left({x}+\mathrm{1}\right)}\:+\frac{\mathrm{17}}{\mathrm{32}\left({x}−\mathrm{3}\right)}\:+\frac{−\frac{\mathrm{15}}{\mathrm{32}}{x}+{d}}{{x}^{\mathrm{2}} −{x}+\mathrm{2}} \\ $$$${F}\left(\mathrm{0}\right)=\frac{−\mathrm{1}}{−\mathrm{6}}\:=\frac{\mathrm{1}}{\mathrm{6}}\:=−\frac{\mathrm{1}}{\mathrm{16}}\:−\frac{\mathrm{17}}{\mathrm{3}.\mathrm{32}}\:+\frac{{d}}{\mathrm{2}}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{3}}\:=−\frac{\mathrm{1}}{\mathrm{8}}\:−\frac{\mathrm{17}}{\mathrm{48}}\:+{d}\:\Rightarrow{d}\:=\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{8}}\:+\frac{\mathrm{17}}{\mathrm{48}} \\ $$$$=\frac{\mathrm{11}}{\mathrm{24}}\:+\frac{\mathrm{17}}{\mathrm{48}}\:=\frac{\mathrm{22}+\mathrm{17}}{\mathrm{48}}\:=\frac{\mathrm{39}}{\mathrm{48}}\:\Rightarrow \\ $$$$\int\:\:\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{3}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)}{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{16}}\int\frac{{dx}}{{x}+\mathrm{1}}\:+\frac{\mathrm{17}}{\mathrm{32}}\int\:\frac{{dx}}{{x}−\mathrm{3}}\:−\frac{\mathrm{15}}{\mathrm{32}}\int\:\:\frac{{x}}{{x}^{\mathrm{2}} −{x}+\mathrm{2}}{dx}\:+\frac{\mathrm{39}}{\mathrm{48}}\:\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{2}}\:+{c} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{16}}{ln}\mid{x}+\mathrm{1}\mid+\frac{\mathrm{17}}{\mathrm{32}}{ln}\mid{x}−\mathrm{3}\mid−\frac{\mathrm{15}}{\mathrm{64}}\:\int\:\frac{\mathrm{2}{x}−\mathrm{1}+\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{2}}{dx}\:+\frac{\mathrm{39}}{\mathrm{48}}\:\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{2}}\:+{c} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{16}}{ln}\mid{x}+\mathrm{1}\mid+\frac{\mathrm{17}}{\mathrm{32}}{ln}\mid{x}−\mathrm{3}\mid−\frac{\mathrm{15}}{\mathrm{64}}{ln}\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)+\left(\frac{\mathrm{39}}{\mathrm{48}}−\frac{\mathrm{15}}{\mathrm{64}}\right)\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{2}}{dx}\:+{c}\:{but} \\ $$$$\int\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{2}}\:=\int\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{2}−\frac{\mathrm{1}}{\mathrm{4}}}\:=\int\:\:\frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{7}}{\mathrm{4}}}\:=_{{x}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}{u}} \frac{\mathrm{4}}{\mathrm{7}}\:\int\:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}{du} \\ $$$$=\frac{\mathrm{2}}{\sqrt{\mathrm{7}}}\:{arctan}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{7}}}\right)\:\Rightarrow \\ $$$$\int\:{F}\left({x}\right){dx}\:=−\frac{\mathrm{1}}{\mathrm{16}}{ln}\mid{x}+\mathrm{1}\mid+\frac{\mathrm{17}}{\mathrm{32}}{ln}\mid{x}−\mathrm{3}\mid−\frac{\mathrm{15}}{\mathrm{64}}{ln}\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)+\left(\frac{\mathrm{39}}{\mathrm{48}}−\frac{\mathrm{15}}{\mathrm{64}}\right)\frac{\mathrm{2}}{\sqrt{\mathrm{7}}}\:{arctan}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{7}}}\right)\:+{c} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com