
Question Number 87833 by M±th+et£s last updated on 06/Apr/20
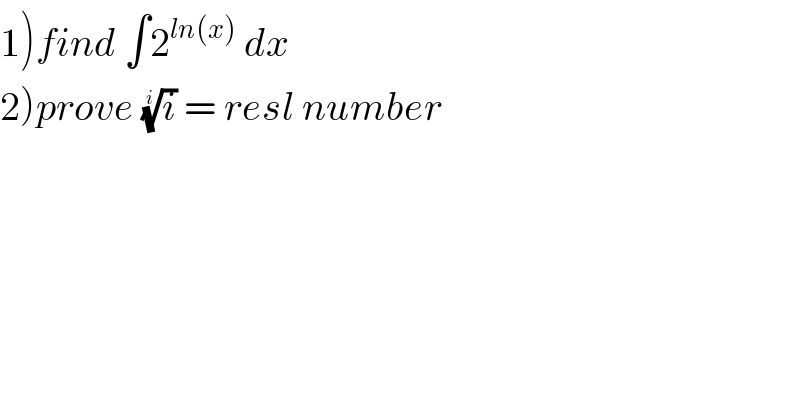
$$\left.\mathrm{1}\right){find}\:\int\mathrm{2}^{{ln}\left({x}\right)} \:{dx} \\ $$$$\left.\mathrm{2}\right){prove}\:\sqrt[{{i}}]{{i}}\:=\:{resl}\:{number} \\ $$
Commented by mr W last updated on 06/Apr/20
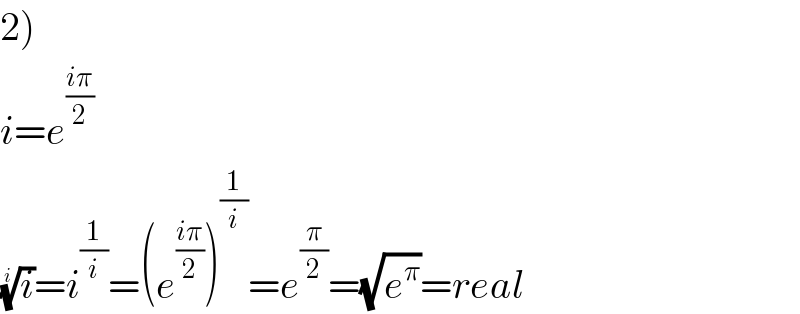
$$\left.\mathrm{2}\right) \\ $$$${i}={e}^{\frac{{i}\pi}{\mathrm{2}}} \\ $$$$\sqrt[{{i}}]{{i}}={i}^{\frac{\mathrm{1}}{{i}}} =\left({e}^{\frac{{i}\pi}{\mathrm{2}}} \right)^{\frac{\mathrm{1}}{{i}}} ={e}^{\frac{\pi}{\mathrm{2}}} =\sqrt{{e}^{\pi} }={real} \\ $$
Commented by john santu last updated on 06/Apr/20
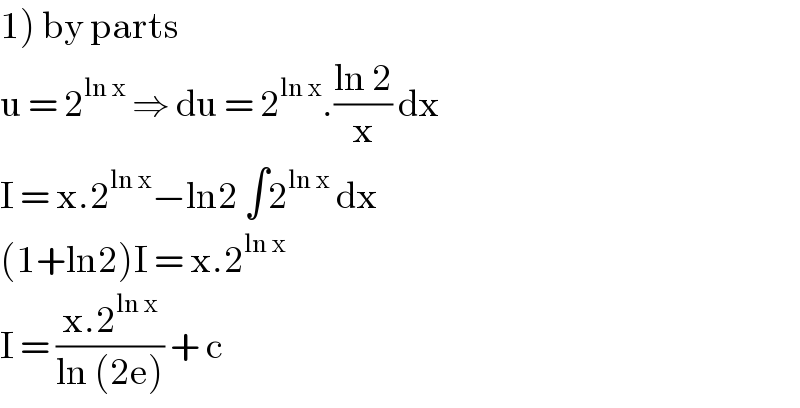
$$\left.\mathrm{1}\right)\:\mathrm{by}\:\mathrm{parts} \\ $$$$\mathrm{u}\:=\:\mathrm{2}^{\mathrm{ln}\:\mathrm{x}} \:\Rightarrow\:\mathrm{du}\:=\:\mathrm{2}^{\mathrm{ln}\:\mathrm{x}} .\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{x}}\:\mathrm{dx}\: \\ $$$$\mathrm{I}\:=\:\mathrm{x}.\mathrm{2}^{\mathrm{ln}\:\mathrm{x}} −\mathrm{ln2}\:\int\mathrm{2}^{\mathrm{ln}\:\mathrm{x}} \:\mathrm{dx}\:\: \\ $$$$\left(\mathrm{1}+\mathrm{ln2}\right)\mathrm{I}\:=\:\mathrm{x}.\mathrm{2}^{\mathrm{ln}\:\mathrm{x}} \: \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{x}.\mathrm{2}^{\mathrm{ln}\:\mathrm{x}} }{\mathrm{ln}\:\left(\mathrm{2e}\right)}\:+\:\mathrm{c} \\ $$
Commented by M±th+et£s last updated on 06/Apr/20

$${thank}\:{you} \\ $$
Commented by M±th+et£s last updated on 06/Apr/20

$${tank}\:{you} \\ $$
Commented by mathmax by abdo last updated on 06/Apr/20
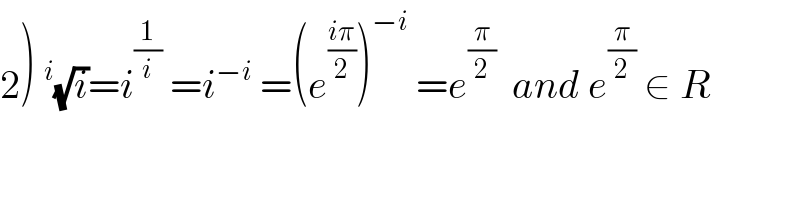
$$\left.\mathrm{2}\right)\:^{{i}} \sqrt{{i}}={i}^{\frac{\mathrm{1}}{{i}}} \:={i}^{−{i}} \:=\left({e}^{\frac{{i}\pi}{\mathrm{2}}} \right)^{−{i}} \:={e}^{\frac{\pi}{\mathrm{2}}} \:\:{and}\:{e}^{\frac{\pi}{\mathrm{2}}} \:\in\:{R} \\ $$
Answered by petrochengula last updated on 06/Apr/20

$$\int\mathrm{2}^{{lnx}} {dx} \\ $$$${e}^{{ln}\mathrm{2}} =\mathrm{2}\:{then}\:\mathrm{2}^{{lnx}} =\left({e}^{{ln}\mathrm{2}} \right)^{{lnx}} =\left(\mathrm{2}^{{lnx}} \right)^{{ln}\mathrm{2}} ={x}^{{ln}\mathrm{2}} \\ $$$$\int\mathrm{2}^{{lnx}} {dx}=\int{x}^{{ln}\mathrm{2}} {dx}=\frac{{x}^{{ln}\mathrm{2}+\mathrm{1}} }{{ln}\mathrm{2}+\mathrm{1}}+{C} \\ $$
