
Question Number 204909 by mnjuly1970 last updated on 01/Mar/24
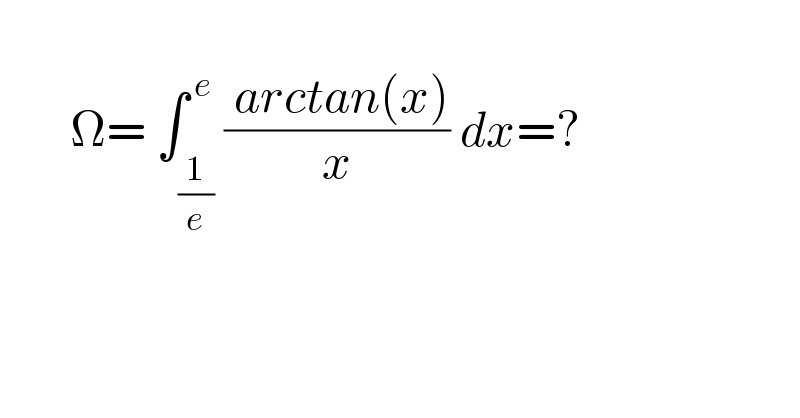
$$ \\ $$$$\:\:\:\:\:\:\:\Omega=\:\int_{\frac{\mathrm{1}}{{e}}} ^{\:{e}} \frac{\:{arctan}\left({x}\right)}{{x}}\:{dx}=? \\ $$
Answered by witcher3 last updated on 01/Mar/24
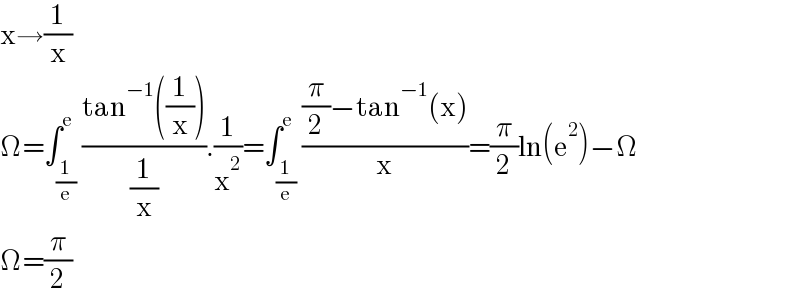
$$\mathrm{x}\rightarrow\frac{\mathrm{1}}{\mathrm{x}} \\ $$$$\Omega=\int_{\frac{\mathrm{1}}{\mathrm{e}}} ^{\mathrm{e}} \frac{\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}}\right)}{\frac{\mathrm{1}}{\mathrm{x}}}.\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }=\int_{\frac{\mathrm{1}}{\mathrm{e}}} ^{\mathrm{e}} \frac{\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)}{\mathrm{x}}=\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\mathrm{e}^{\mathrm{2}} \right)−\Omega \\ $$$$\Omega=\frac{\pi}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 01/Mar/24

$$\:\cancel{\lesseqgtr} \\ $$
Commented by witcher3 last updated on 01/Mar/24

$$\mathrm{withe}\:\mathrm{Pleasur}\:\mathrm{Sir} \\ $$
