Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 130138 by mathmax by abdo last updated on 22/Jan/21

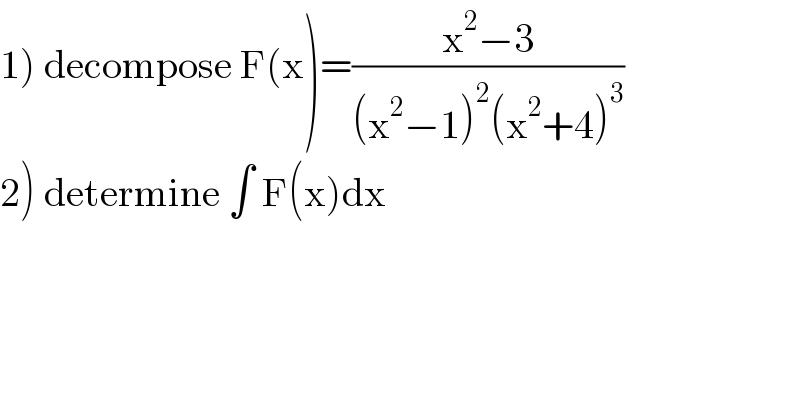
1) decompose F(x)=((x^2 −3)/((x^2 −1)^2 (x^2 +4)^3 )) 2) determine ∫ F(x)dx

$$\left.\mathrm{1}\right)\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{3}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{3}} } \\ $$$$\left.\mathrm{2}\right)\:\mathrm{determine}\:\int\:\mathrm{F}\left(\mathrm{x}\right)\mathrm{dx} \\ $$

Answered by MJS_new last updated on 23/Jan/21

decomposition ∫((x^2 −3)/((x^2 −1)^2 (x^2 +4)^3 ))dx= =∫(−(1/(250(x−1)^2 ))+(8/(625(x−1)))−(1/(250(x+1)^2 ))−(8/(625(x+1)))−(7/(25(x^2 +4)^3 ))−(9/(125(x^2 +4)^2 ))−((11)/(625(x^2 +4))))dx ... Ostrogradski ∫((x^2 −3)/((x^2 −1)^2 (x^2 +4)^3 ))dx= =−((x(121x^4 +3x^2 −3324))/(16000(x^2 −1)(x^2 +4)^2 ))−(1/(16000))∫((121x^2 −2169)/((x^2 −1)(x^2 +4)))dx= =...+(8/(625))∫(dx/(x−1))−(8/(625))∫(dx/(x+1))−((2653)/(80000))∫(dx/(x^2 +4))= ... =−((x(121x^4 +3x^2 −3324))/(16000(x^2 −1)(x^2 +4)^2 ))+(8/(625))ln ∣((x−1)/(x+1))∣ −((2653)/(160000))arctan (x/2) +C

$$\mathrm{decomposition} \\ $$$$\int\frac{{x}^{\mathrm{2}} −\mathrm{3}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{3}} }{dx}= \\ $$$$=\int\left(−\frac{\mathrm{1}}{\mathrm{250}\left({x}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{8}}{\mathrm{625}\left({x}−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{250}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{8}}{\mathrm{625}\left({x}+\mathrm{1}\right)}−\frac{\mathrm{7}}{\mathrm{25}\left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{3}} }−\frac{\mathrm{9}}{\mathrm{125}\left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} }−\frac{\mathrm{11}}{\mathrm{625}\left({x}^{\mathrm{2}} +\mathrm{4}\right)}\right){dx} \\ $$$$... \\ $$$$ \\ $$$$\mathrm{Ostrogradski} \\ $$$$\int\frac{{x}^{\mathrm{2}} −\mathrm{3}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{3}} }{dx}= \\ $$$$=−\frac{{x}\left(\mathrm{121}{x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3324}\right)}{\mathrm{16000}\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{16000}}\int\frac{\mathrm{121}{x}^{\mathrm{2}} −\mathrm{2169}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{4}\right)}{dx}= \\ $$$$=...+\frac{\mathrm{8}}{\mathrm{625}}\int\frac{{dx}}{{x}−\mathrm{1}}−\frac{\mathrm{8}}{\mathrm{625}}\int\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{2653}}{\mathrm{80000}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{4}}= \\ $$$$... \\ $$$$=−\frac{{x}\left(\mathrm{121}{x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3324}\right)}{\mathrm{16000}\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} }+\frac{\mathrm{8}}{\mathrm{625}}\mathrm{ln}\:\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\mid\:−\frac{\mathrm{2653}}{\mathrm{160000}}\mathrm{arctan}\:\frac{{x}}{\mathrm{2}}\:+{C} \\ $$

Commented by mathmax by abdo last updated on 23/Jan/21

thank you sir.

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by Lordose last updated on 23/Jan/21

Sir is there any software capable of solving the variables in applying ostrograski

$$\mathrm{Sir}\:\mathrm{is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{software}\:\mathrm{capable}\:\mathrm{of}\:\mathrm{solving} \\ $$$$\mathrm{the}\:\mathrm{variables}\:\mathrm{in}\:\mathrm{applying}\:\mathrm{ostrograski}\: \\ $$

Commented by MJS_new last updated on 23/Jan/21

I don′t know...

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com