
Question Number 102303 by bemath last updated on 08/Jul/20
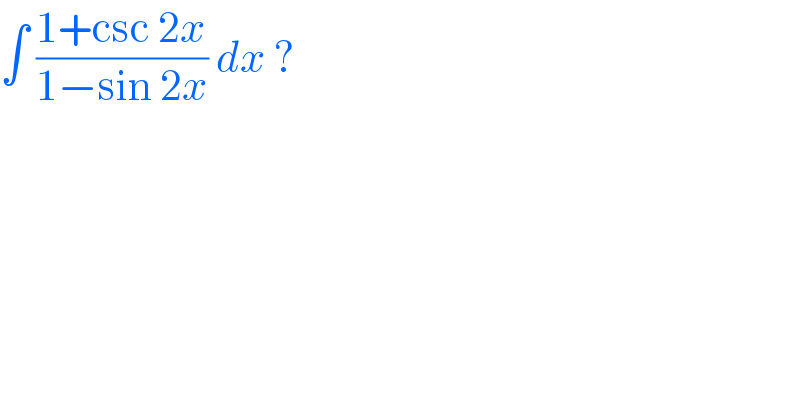
$$\int\:\frac{\mathrm{1}+\mathrm{csc}\:\mathrm{2}{x}}{\mathrm{1}−\mathrm{sin}\:\mathrm{2}{x}}\:{dx}\:? \\ $$
Commented by bemath last updated on 08/Jul/20

$${thank}\:{you}\:{both} \\ $$
Answered by 1549442205 last updated on 08/Jul/20
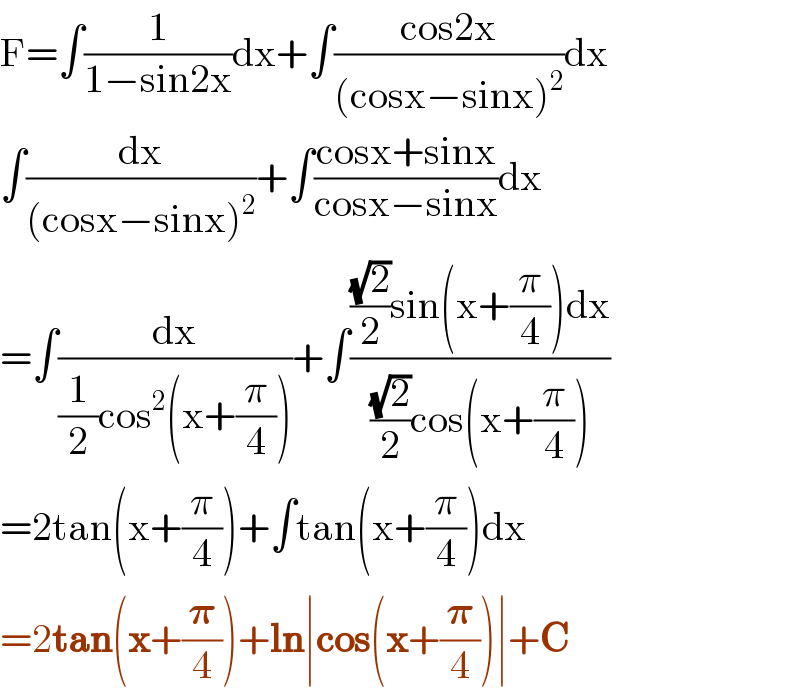
$$\mathrm{F}=\int\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin2x}}\mathrm{dx}+\int\frac{\mathrm{cos2x}}{\left(\mathrm{cosx}−\mathrm{sinx}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\int\frac{\mathrm{dx}}{\left(\mathrm{cosx}−\mathrm{sinx}\right)^{\mathrm{2}} }+\int\frac{\mathrm{cosx}+\mathrm{sinx}}{\mathrm{cosx}−\mathrm{sinx}}\mathrm{dx} \\ $$$$=\int\frac{\mathrm{dx}}{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)}+\int\frac{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)\mathrm{dx}}{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{cos}\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)} \\ $$$$=\mathrm{2tan}\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)+\int\mathrm{tan}\left(\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)\mathrm{dx} \\ $$$$=\mathrm{2}\boldsymbol{\mathrm{tan}}\left(\boldsymbol{\mathrm{x}}+\frac{\boldsymbol{\pi}}{\mathrm{4}}\right)+\boldsymbol{\mathrm{ln}}\mid\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}+\frac{\boldsymbol{\pi}}{\mathrm{4}}\right)\mid+\boldsymbol{\mathrm{C}} \\ $$
Answered by Dwaipayan Shikari last updated on 08/Jul/20
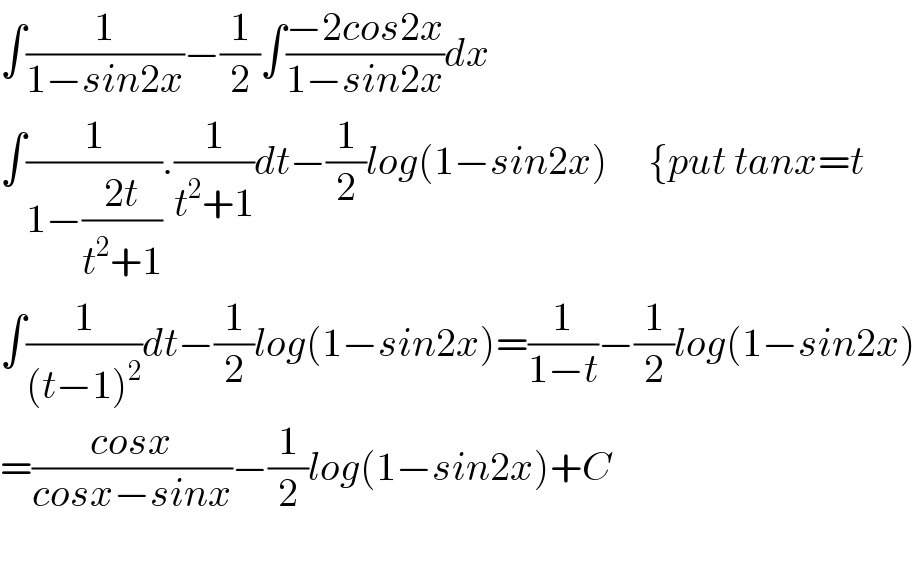
$$\int\frac{\mathrm{1}}{\mathrm{1}−{sin}\mathrm{2}{x}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{−\mathrm{2}{cos}\mathrm{2}{x}}{\mathrm{1}−{sin}\mathrm{2}{x}}{dx} \\ $$$$\int\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}}.\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}−\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{1}−{sin}\mathrm{2}{x}\right)\:\:\:\:\:\left\{{put}\:{tanx}={t}\right. \\ $$$$\int\frac{\mathrm{1}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }{dt}−\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{1}−{sin}\mathrm{2}{x}\right)=\frac{\mathrm{1}}{\mathrm{1}−{t}}−\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{1}−{sin}\mathrm{2}{x}\right) \\ $$$$=\frac{{cosx}}{{cosx}−{sinx}}−\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{1}−{sin}\mathrm{2}{x}\right)+{C} \\ $$$$ \\ $$
