
Question Number 101554 by student work last updated on 03/Jul/20
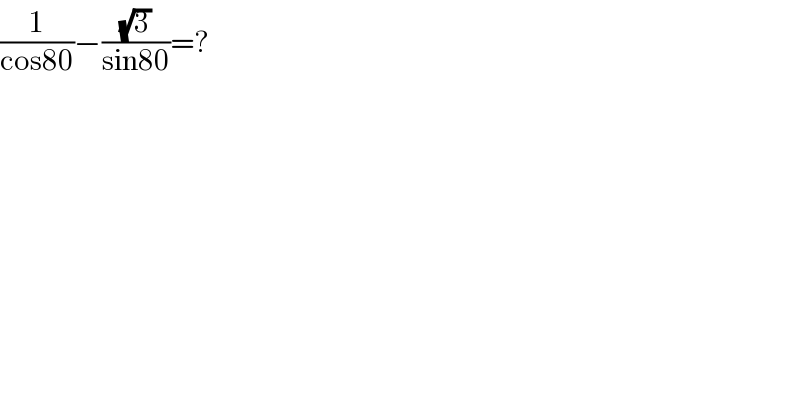
$$\frac{\mathrm{1}}{\mathrm{cos80}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{sin80}}=? \\ $$
Answered by bramlex last updated on 03/Jul/20
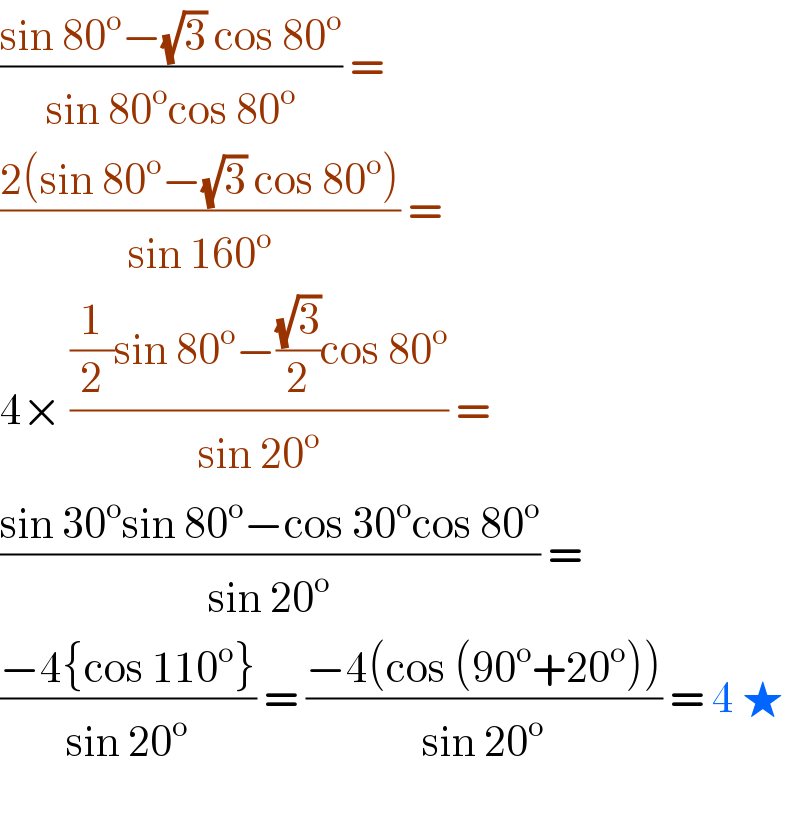
$$\frac{\mathrm{sin}\:\mathrm{80}^{\mathrm{o}} −\sqrt{\mathrm{3}}\:\mathrm{cos}\:\mathrm{80}^{\mathrm{o}} }{\mathrm{sin}\:\mathrm{80}^{\mathrm{o}} \mathrm{cos}\:\mathrm{80}^{\mathrm{o}} }\:=\: \\ $$$$\frac{\mathrm{2}\left(\mathrm{sin}\:\mathrm{80}^{\mathrm{o}} −\sqrt{\mathrm{3}}\:\mathrm{cos}\:\mathrm{80}^{\mathrm{o}} \right)}{\mathrm{sin}\:\mathrm{160}^{\mathrm{o}} }\:=\: \\ $$$$\mathrm{4}×\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{80}^{\mathrm{o}} −\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:\mathrm{80}^{\mathrm{o}} }{\mathrm{sin}\:\mathrm{20}^{\mathrm{o}} }\:= \\ $$$$\frac{\mathrm{sin}\:\mathrm{30}^{\mathrm{o}} \mathrm{sin}\:\mathrm{80}^{\mathrm{o}} −\mathrm{cos}\:\mathrm{30}^{\mathrm{o}} \mathrm{cos}\:\mathrm{80}^{\mathrm{o}} }{\mathrm{sin}\:\mathrm{20}^{\mathrm{o}} }\:= \\ $$$$\frac{−\mathrm{4}\left\{\mathrm{cos}\:\mathrm{110}^{\mathrm{o}} \right\}}{\mathrm{sin}\:\mathrm{20}^{\mathrm{o}} }\:=\:\frac{−\mathrm{4}\left(\mathrm{cos}\:\left(\mathrm{90}^{\mathrm{o}} +\mathrm{20}^{\mathrm{o}} \right)\right)}{\mathrm{sin}\:\mathrm{20}^{\mathrm{o}} }\:=\:\mathrm{4}\:\bigstar \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 03/Jul/20
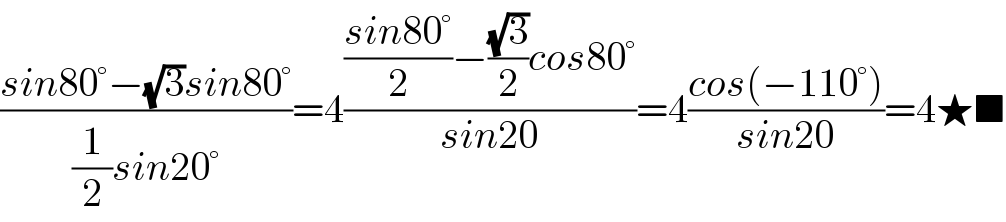
$$\frac{{sin}\mathrm{80}°−\sqrt{\mathrm{3}}{sin}\mathrm{80}°}{\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{20}°}=\mathrm{4}\frac{\frac{{sin}\mathrm{80}°}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{cos}\mathrm{80}°}{{sin}\mathrm{20}}=\mathrm{4}\frac{{cos}\left(−\mathrm{110}°\right)}{{sin}\mathrm{20}}=\mathrm{4}\bigstar\blacksquare \\ $$
Answered by mahdi last updated on 03/Jul/20
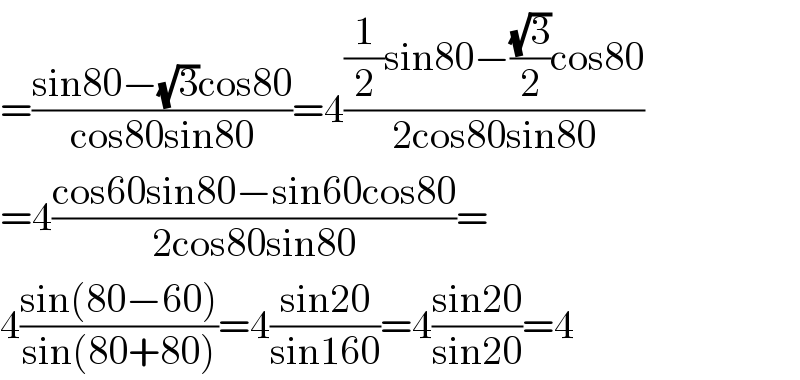
$$=\frac{\mathrm{sin80}−\sqrt{\mathrm{3}}\mathrm{cos80}}{\mathrm{cos80sin80}}=\mathrm{4}\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin80}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos80}}{\mathrm{2cos80sin80}} \\ $$$$=\mathrm{4}\frac{\mathrm{cos60sin80}−\mathrm{sin60cos80}}{\mathrm{2cos80sin80}}= \\ $$$$\mathrm{4}\frac{\mathrm{sin}\left(\mathrm{80}−\mathrm{60}\right)}{\mathrm{sin}\left(\mathrm{80}+\mathrm{80}\right)}=\mathrm{4}\frac{\mathrm{sin20}}{\mathrm{sin160}}=\mathrm{4}\frac{\mathrm{sin20}}{\mathrm{sin20}}=\mathrm{4} \\ $$
