
Question Number 185935 by cortano1 last updated on 30/Jan/23
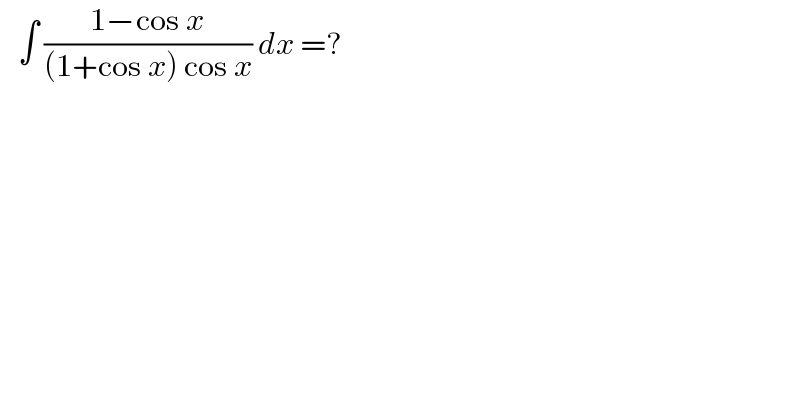
$$\:\:\:\int\:\frac{\mathrm{1}−\mathrm{cos}\:{x}}{\left(\mathrm{1}+\mathrm{cos}\:{x}\right)\:\mathrm{cos}\:{x}}\:{dx}\:=? \\ $$
Answered by Ar Brandon last updated on 30/Jan/23
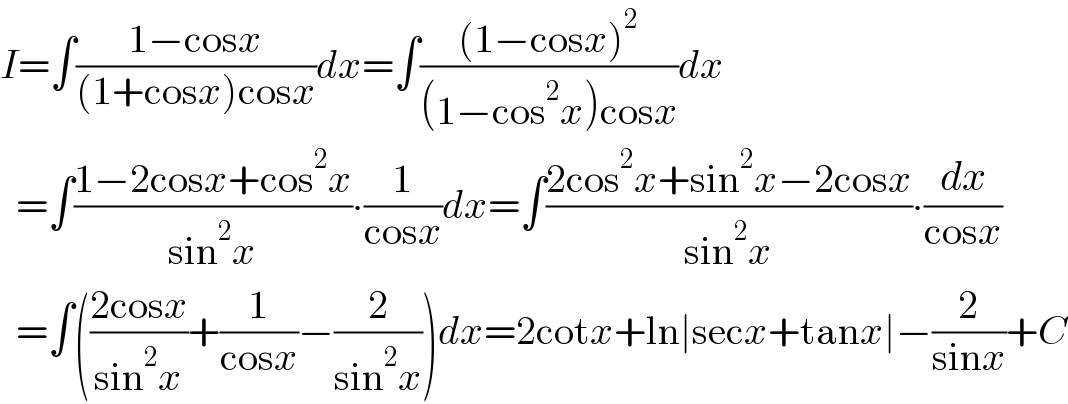
$${I}=\int\frac{\mathrm{1}−\mathrm{cos}{x}}{\left(\mathrm{1}+\mathrm{cos}{x}\right)\mathrm{cos}{x}}{dx}=\int\frac{\left(\mathrm{1}−\mathrm{cos}{x}\right)^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} {x}\right)\mathrm{cos}{x}}{dx} \\ $$$$\:\:=\int\frac{\mathrm{1}−\mathrm{2cos}{x}+\mathrm{cos}^{\mathrm{2}} {x}}{\mathrm{sin}^{\mathrm{2}} {x}}\centerdot\frac{\mathrm{1}}{\mathrm{cos}{x}}{dx}=\int\frac{\mathrm{2cos}^{\mathrm{2}} {x}+\mathrm{sin}^{\mathrm{2}} {x}−\mathrm{2cos}{x}}{\mathrm{sin}^{\mathrm{2}} {x}}\centerdot\frac{{dx}}{\mathrm{cos}{x}} \\ $$$$\:\:=\int\left(\frac{\mathrm{2cos}{x}}{\mathrm{sin}^{\mathrm{2}} {x}}+\frac{\mathrm{1}}{\mathrm{cos}{x}}−\frac{\mathrm{2}}{\mathrm{sin}^{\mathrm{2}} {x}}\right){dx}=\mathrm{2cot}{x}+\mathrm{ln}\mid\mathrm{sec}{x}+\mathrm{tan}{x}\mid−\frac{\mathrm{2}}{\mathrm{sin}{x}}+{C} \\ $$
Answered by ajfour last updated on 30/Jan/23
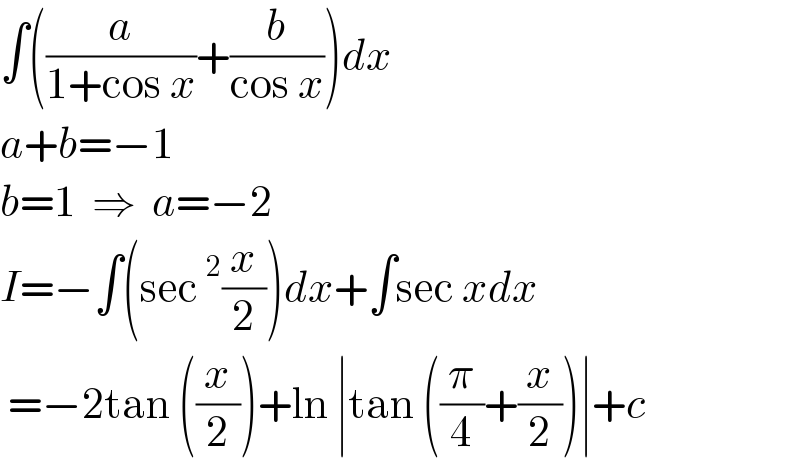
$$\int\left(\frac{{a}}{\mathrm{1}+\mathrm{cos}\:{x}}+\frac{{b}}{\mathrm{cos}\:{x}}\right){dx} \\ $$$${a}+{b}=−\mathrm{1} \\ $$$${b}=\mathrm{1}\:\:\Rightarrow\:\:{a}=−\mathrm{2} \\ $$$${I}=−\int\left(\mathrm{sec}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\right){dx}+\int\mathrm{sec}\:{xdx} \\ $$$$\:=−\mathrm{2tan}\:\left(\frac{{x}}{\mathrm{2}}\right)+\mathrm{ln}\:\mid\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}+\frac{{x}}{\mathrm{2}}\right)\mid+{c} \\ $$
Commented by ARUNG_Brandon_MBU last updated on 30/Jan/23
Nice
