
Question Number 96782 by M±th+et+s last updated on 04/Jun/20
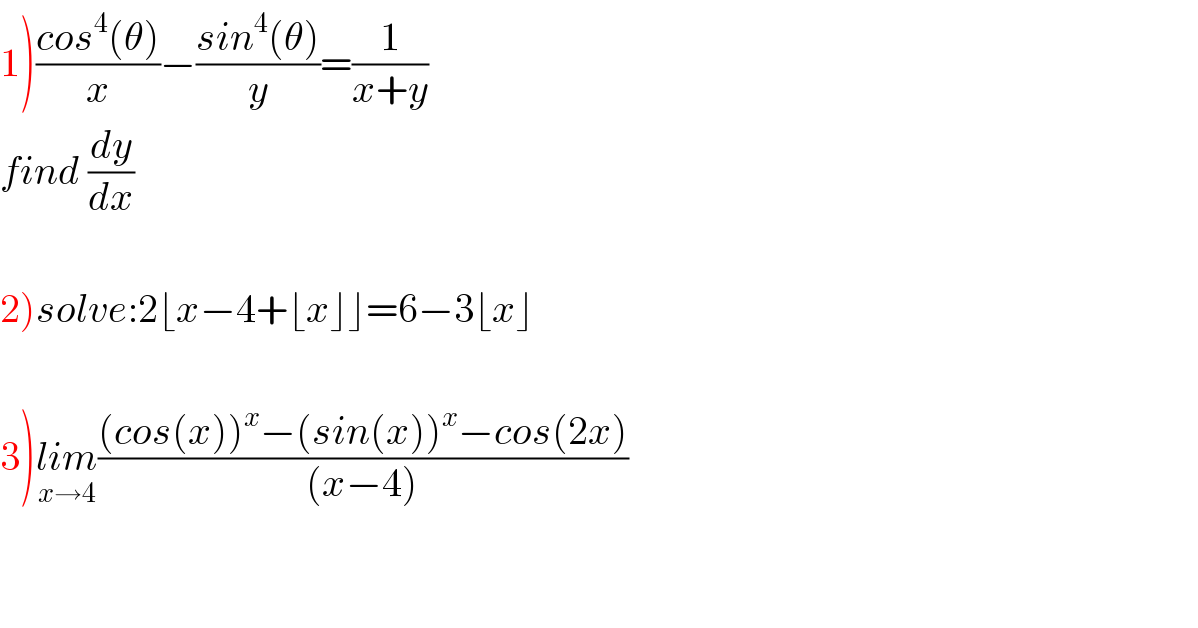
$$\left.\mathrm{1}\right)\frac{{cos}^{\mathrm{4}} \left(\theta\right)}{{x}}−\frac{{sin}^{\mathrm{4}} \left(\theta\right)}{{y}}=\frac{\mathrm{1}}{{x}+{y}} \\ $$$${find}\:\frac{{dy}}{{dx}} \\ $$$$ \\ $$$$\left.\mathrm{2}\right){solve}:\mathrm{2}\lfloor{x}−\mathrm{4}+\lfloor{x}\rfloor\rfloor=\mathrm{6}−\mathrm{3}\lfloor{x}\rfloor \\ $$$$ \\ $$$$\left.\mathrm{3}\right)\underset{{x}\rightarrow\mathrm{4}} {{lim}}\frac{\left({cos}\left({x}\right)\right)^{{x}} −\left({sin}\left({x}\right)\right)^{{x}} −{cos}\left(\mathrm{2}{x}\right)}{\left({x}−\mathrm{4}\right)} \\ $$$$ \\ $$$$ \\ $$
Commented by M±th+et+s last updated on 04/Jun/20
$${thanks}\:{for}\:{solutions} \\ $$
Answered by mr W last updated on 04/Jun/20
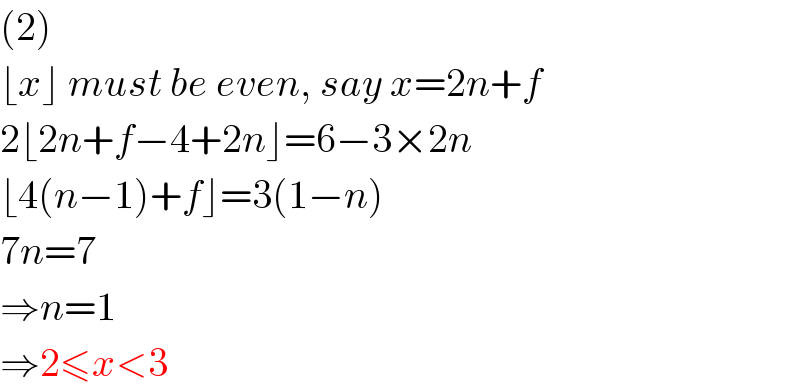
$$\left(\mathrm{2}\right) \\ $$$$\lfloor{x}\rfloor\:{must}\:{be}\:{even},\:{say}\:{x}=\mathrm{2}{n}+{f} \\ $$$$\mathrm{2}\lfloor\mathrm{2}{n}+{f}−\mathrm{4}+\mathrm{2}{n}\rfloor=\mathrm{6}−\mathrm{3}×\mathrm{2}{n} \\ $$$$\lfloor\mathrm{4}\left({n}−\mathrm{1}\right)+{f}\rfloor=\mathrm{3}\left(\mathrm{1}−{n}\right) \\ $$$$\mathrm{7}{n}=\mathrm{7} \\ $$$$\Rightarrow{n}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}\leqslant{x}<\mathrm{3} \\ $$
Answered by Sourav mridha last updated on 04/Jun/20
![(3)(0/0)form so using L′Ho^� pital Ans:cos^4 (4)[−4tan(4)+ln(cos(4))] −sin^4 (4)[4cot(4)+ln(sin(4))] +2sin(8)..](Q96801.png)
$$\left(\mathrm{3}\right)\frac{\mathrm{0}}{\mathrm{0}}\boldsymbol{{form}}\:\boldsymbol{{so}}\:\boldsymbol{{using}}\:\boldsymbol{{L}}'\boldsymbol{{H}}\hat {\mathrm{o}}\boldsymbol{{pital}} \\ $$$$\boldsymbol{{Ans}}:\boldsymbol{{cos}}^{\mathrm{4}} \left(\mathrm{4}\right)\left[−\mathrm{4}\boldsymbol{{tan}}\left(\mathrm{4}\right)+\boldsymbol{{ln}}\left(\boldsymbol{{cos}}\left(\mathrm{4}\right)\right)\right] \\ $$$$\:\:\:\:\:\:\:−\boldsymbol{{sin}}^{\mathrm{4}} \left(\mathrm{4}\right)\left[\mathrm{4}\boldsymbol{{cot}}\left(\mathrm{4}\right)+\boldsymbol{{ln}}\left(\boldsymbol{{sin}}\left(\mathrm{4}\right)\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:+\mathrm{2}\boldsymbol{{sin}}\left(\mathrm{8}\right).. \\ $$
Answered by abdomathmax last updated on 05/Jun/20
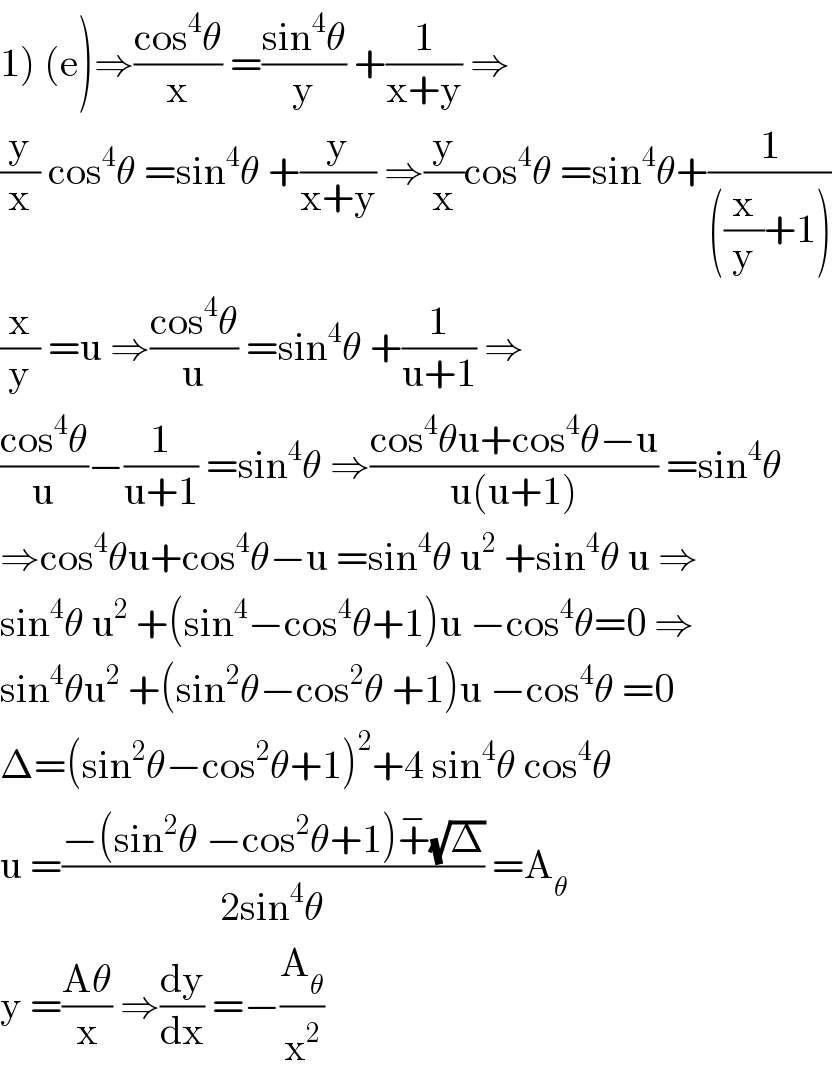
$$\left.\mathrm{1}\right)\:\left(\mathrm{e}\right)\Rightarrow\frac{\mathrm{cos}^{\mathrm{4}} \theta}{\mathrm{x}}\:=\frac{\mathrm{sin}^{\mathrm{4}} \theta}{\mathrm{y}}\:+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{y}}\:\Rightarrow \\ $$$$\frac{\mathrm{y}}{\mathrm{x}}\:\mathrm{cos}^{\mathrm{4}} \theta\:=\mathrm{sin}^{\mathrm{4}} \theta\:+\frac{\mathrm{y}}{\mathrm{x}+\mathrm{y}}\:\Rightarrow\frac{\mathrm{y}}{\mathrm{x}}\mathrm{cos}^{\mathrm{4}} \theta\:=\mathrm{sin}^{\mathrm{4}} \theta+\frac{\mathrm{1}}{\left(\frac{\mathrm{x}}{\mathrm{y}}+\mathrm{1}\right)} \\ $$$$\frac{\mathrm{x}}{\mathrm{y}}\:=\mathrm{u}\:\Rightarrow\frac{\mathrm{cos}^{\mathrm{4}} \theta}{\mathrm{u}}\:=\mathrm{sin}^{\mathrm{4}} \theta\:+\frac{\mathrm{1}}{\mathrm{u}+\mathrm{1}}\:\Rightarrow \\ $$$$\frac{\mathrm{cos}^{\mathrm{4}} \theta}{\mathrm{u}}−\frac{\mathrm{1}}{\mathrm{u}+\mathrm{1}}\:=\mathrm{sin}^{\mathrm{4}} \theta\:\Rightarrow\frac{\mathrm{cos}^{\mathrm{4}} \theta\mathrm{u}+\mathrm{cos}^{\mathrm{4}} \theta−\mathrm{u}}{\mathrm{u}\left(\mathrm{u}+\mathrm{1}\right)}\:=\mathrm{sin}^{\mathrm{4}} \theta \\ $$$$\Rightarrow\mathrm{cos}^{\mathrm{4}} \theta\mathrm{u}+\mathrm{cos}^{\mathrm{4}} \theta−\mathrm{u}\:=\mathrm{sin}^{\mathrm{4}} \theta\:\mathrm{u}^{\mathrm{2}} \:+\mathrm{sin}^{\mathrm{4}} \theta\:\mathrm{u}\:\Rightarrow \\ $$$$\mathrm{sin}^{\mathrm{4}} \theta\:\mathrm{u}^{\mathrm{2}} \:+\left(\mathrm{sin}^{\mathrm{4}} −\mathrm{cos}^{\mathrm{4}} \theta+\mathrm{1}\right)\mathrm{u}\:−\mathrm{cos}^{\mathrm{4}} \theta=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{sin}^{\mathrm{4}} \theta\mathrm{u}^{\mathrm{2}} \:+\left(\mathrm{sin}^{\mathrm{2}} \theta−\mathrm{cos}^{\mathrm{2}} \theta\:+\mathrm{1}\right)\mathrm{u}\:−\mathrm{cos}^{\mathrm{4}} \theta\:=\mathrm{0} \\ $$$$\Delta=\left(\mathrm{sin}^{\mathrm{2}} \theta−\mathrm{cos}^{\mathrm{2}} \theta+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}\:\mathrm{sin}^{\mathrm{4}} \theta\:\mathrm{cos}^{\mathrm{4}} \theta \\ $$$$\mathrm{u}\:=\frac{−\left(\mathrm{sin}^{\mathrm{2}} \theta\:−\mathrm{cos}^{\mathrm{2}} \theta+\mathrm{1}\right)\overset{−} {+}\sqrt{\Delta}}{\mathrm{2sin}^{\mathrm{4}} \theta}\:=\mathrm{A}_{\theta} \\ $$$$\mathrm{y}\:=\frac{\mathrm{A}\theta}{\mathrm{x}}\:\Rightarrow\frac{\mathrm{dy}}{\mathrm{dx}}\:=−\frac{\mathrm{A}_{\theta} }{\mathrm{x}^{\mathrm{2}} } \\ $$
Commented by abdomathmax last updated on 05/Jun/20
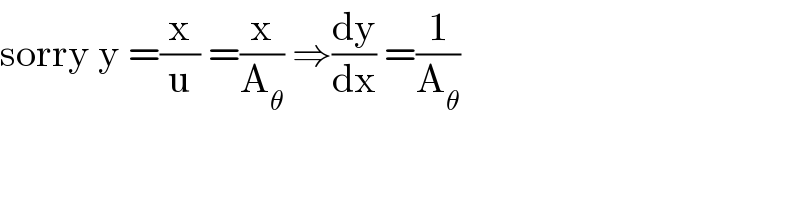
$$\mathrm{sorry}\:\mathrm{y}\:=\frac{\mathrm{x}}{\mathrm{u}}\:=\frac{\mathrm{x}}{\mathrm{A}_{\theta} }\:\Rightarrow\frac{\mathrm{dy}}{\mathrm{dx}}\:=\frac{\mathrm{1}}{\mathrm{A}_{\theta} } \\ $$
Commented by M±th+et+s last updated on 05/Jun/20

$${well}\:{done}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 05/Jun/20

$$\mathrm{thankx} \\ $$
