
Question Number 84868 by jagoll last updated on 17/Mar/20
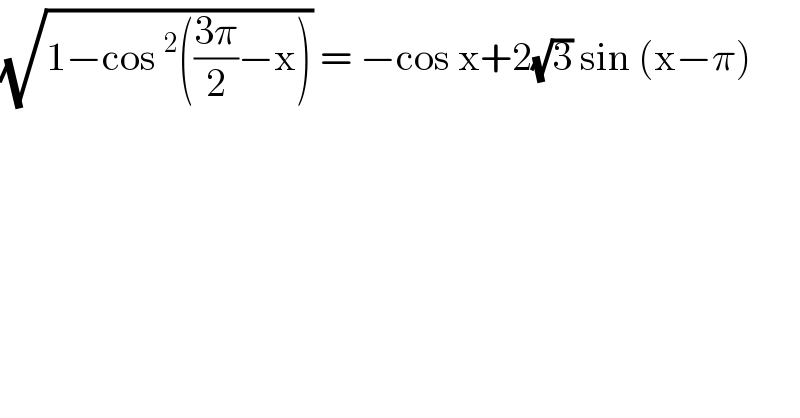
$$\sqrt{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \left(\frac{\mathrm{3}\pi}{\mathrm{2}}−\mathrm{x}\right)}\:=\:−\mathrm{cos}\:\mathrm{x}+\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{sin}\:\left(\mathrm{x}−\pi\right) \\ $$
Answered by john santu last updated on 17/Mar/20
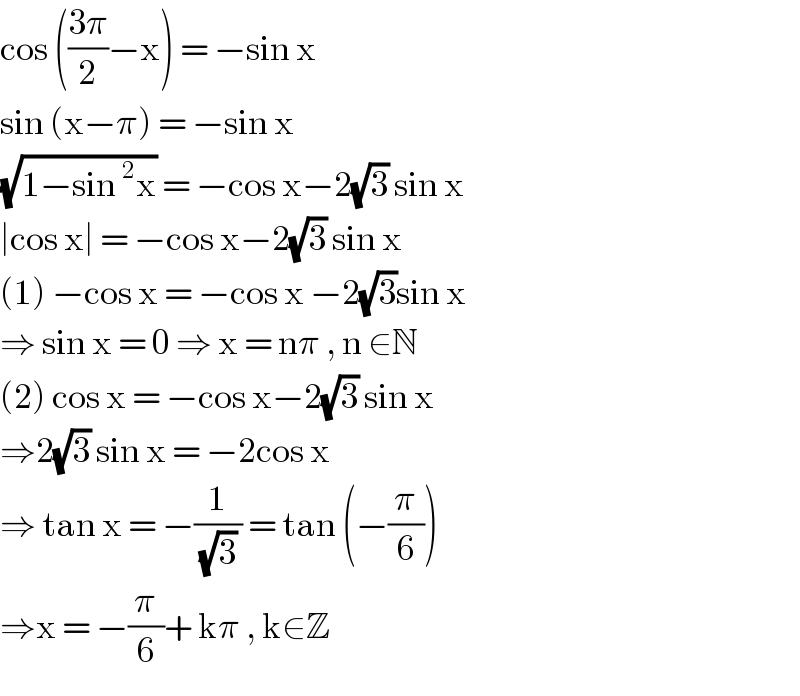
$$\mathrm{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{2}}−\mathrm{x}\right)\:=\:−\mathrm{sin}\:\mathrm{x} \\ $$$$\mathrm{sin}\:\left(\mathrm{x}−\pi\right)\:=\:−\mathrm{sin}\:\mathrm{x} \\ $$$$\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}\:=\:−\mathrm{cos}\:\mathrm{x}−\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{x} \\ $$$$\mid\mathrm{cos}\:\mathrm{x}\mid\:=\:−\mathrm{cos}\:\mathrm{x}−\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{x} \\ $$$$\left(\mathrm{1}\right)\:−\mathrm{cos}\:\mathrm{x}\:=\:−\mathrm{cos}\:\mathrm{x}\:−\mathrm{2}\sqrt{\mathrm{3}}\mathrm{sin}\:\mathrm{x} \\ $$$$\Rightarrow\:\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{0}\:\Rightarrow\:\mathrm{x}\:=\:\mathrm{n}\pi\:,\:\mathrm{n}\:\in\mathbb{N} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{cos}\:\mathrm{x}\:=\:−\mathrm{cos}\:\mathrm{x}−\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{x} \\ $$$$\Rightarrow\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{x}\:=\:−\mathrm{2cos}\:\mathrm{x}\: \\ $$$$\Rightarrow\:\mathrm{tan}\:\mathrm{x}\:=\:−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}\:}\:=\:\mathrm{tan}\:\left(−\frac{\pi}{\mathrm{6}}\right) \\ $$$$\Rightarrow\mathrm{x}\:=\:−\frac{\pi}{\mathrm{6}}+\:\mathrm{k}\pi\:,\:\mathrm{k}\in\mathbb{Z}\: \\ $$
Commented by jagoll last updated on 17/Mar/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
