
Question Number 77755 by abdomathmax last updated on 09/Jan/20
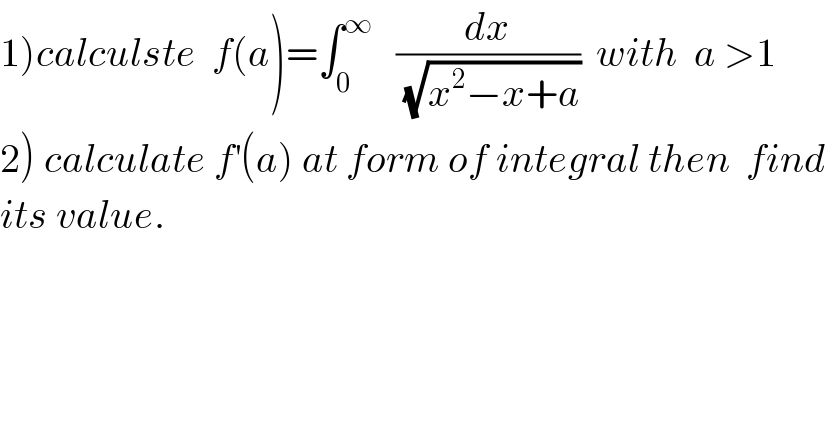
$$\left.\mathrm{1}\right){calculste}\:\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\sqrt{{x}^{\mathrm{2}} −{x}+{a}}}\:\:{with}\:\:{a}\:>\mathrm{1} \\ $$ $$\left.\mathrm{2}\right)\:{calculate}\:{f}^{'} \left({a}\right)\:{at}\:{form}\:{of}\:{integral}\:{then}\:\:{find} \\ $$ $${its}\:{value}. \\ $$ $$ \\ $$ $$ \\ $$
Commented bymathmax by abdo last updated on 11/Jan/20
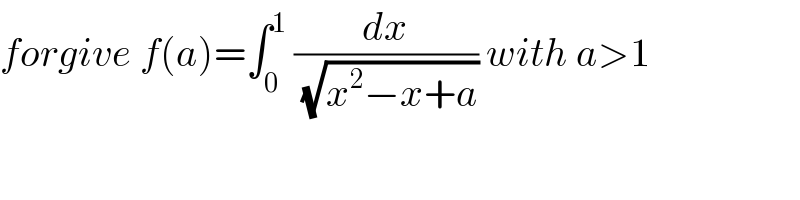
$${forgive}\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{\sqrt{{x}^{\mathrm{2}} −{x}+{a}}}\:{with}\:{a}>\mathrm{1} \\ $$
Commented bymathmax by abdo last updated on 11/Jan/20
![f(a)=∫_0 ^1 (dx/(√(x^2 −x+a))) we have x^2 −x+a=x^2 −2(x/2)+(1/4)+a−(1/4) =(x−(1/2))^2 +((4a−1)/4) and ((4a−1)/4)>0 fhangement x−(1/2)=((√(4a−1))/2)u give f(a) =∫_(−(1/(√(4a−1)))) ^(1/(√(4a−1))) (1/(((√(4a−1))/2)((√(1+u^2 ))))×((√(4a−1))/2)du =∫_((−1)/(√(4a−1))) ^(1/(√(4a−1))) (du/(√(1+u^2 ))) =2 ∫_0 ^(1/(√(4a−1))) (du/(√(1+u^2 ))) =2[ln(u+(√(=u^2 +1)))]_0 ^(1/(√(4a−1))) =2{ln((1/(√(4a−1)))+(√((1/(4a−1 ))+1)))}=2 ln((1/(√(4a−1)))+((2(√a))/(√(4a−1)))) =2ln(((2(√a)+1)/(√(4a−1)))) =2ln(2(√a)+1)−ln(4a−1) ⇒f(a)=2ln(2(√a)+1)−ln(4a−1) 2) we have f^′ (a)=∫_0 ^1 (∂/∂a)((1/(√(x^2 −x+a))))dx =∫_0 ^1 (∂/∂a){( x^2 −x+a)^(−(1/2)) }dx =∫_0 ^1 −(1/2)(x^2 −x+a)^(−(3/2)) dx =−(1/2)∫_0 ^1 (dx/((x^2 −x+a)(√(x^2 −x+a)))) from another side f^′ (a) =2 ×((1/(√a))/(2(√a)+1))−(4/(4a−1)) =2×(1/((√a)(2(√a)+1)))−(4/(4a−1)) =(2/(2a+(√a)))−(4/(4a−1)) ⇒ −(1/2)∫_0 ^1 (dx/((x^2 −x+a)(√(x^2 −x+a)))) =(2/(2a+(√a)))−(4/(4a−1)) also we get ∫_0 ^1 (dx/((x^2 −x+a)(√(x^2 −x+a)))) =((−4)/(2a+(√a)))+(8/(4a−1))](Q77884.png)
$${f}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{\sqrt{{x}^{\mathrm{2}} −{x}+{a}}}\:\:{we}\:{have}\:{x}^{\mathrm{2}} −{x}+{a}={x}^{\mathrm{2}} −\mathrm{2}\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+{a}−\frac{\mathrm{1}}{\mathrm{4}} \\ $$ $$=\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{4}{a}−\mathrm{1}}{\mathrm{4}}\:\:{and}\:\frac{\mathrm{4}{a}−\mathrm{1}}{\mathrm{4}}>\mathrm{0}\:\:{fhangement}\:{x}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{4}{a}−\mathrm{1}}}{\mathrm{2}}{u} \\ $$ $${give}\:{f}\left({a}\right)\:=\int_{−\frac{\mathrm{1}}{\sqrt{\mathrm{4}{a}−\mathrm{1}}}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{4}{a}−\mathrm{1}}}} \:\frac{\mathrm{1}}{\frac{\sqrt{\mathrm{4}{a}−\mathrm{1}}}{\mathrm{2}}\left(\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }\right.}×\frac{\sqrt{\mathrm{4}{a}−\mathrm{1}}}{\mathrm{2}}{du} \\ $$ $$=\int_{\frac{−\mathrm{1}}{\sqrt{\mathrm{4}{a}−\mathrm{1}}}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{4}{a}−\mathrm{1}}}} \:\frac{{du}}{\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{4}{a}−\mathrm{1}}}} \frac{{du}}{\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }}\:=\mathrm{2}\left[{ln}\left({u}+\sqrt{={u}^{\mathrm{2}} +\mathrm{1}}\right)\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\sqrt{\mathrm{4}{a}−\mathrm{1}}}} \\ $$ $$=\mathrm{2}\left\{{ln}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{4}{a}−\mathrm{1}}}+\sqrt{\frac{\mathrm{1}}{\mathrm{4}{a}−\mathrm{1}\:}+\mathrm{1}}\right)\right\}=\mathrm{2}\:{ln}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{4}{a}−\mathrm{1}}}+\frac{\mathrm{2}\sqrt{{a}}}{\sqrt{\mathrm{4}{a}−\mathrm{1}}}\right) \\ $$ $$=\mathrm{2}{ln}\left(\frac{\mathrm{2}\sqrt{{a}}+\mathrm{1}}{\sqrt{\mathrm{4}{a}−\mathrm{1}}}\right)\:=\mathrm{2}{ln}\left(\mathrm{2}\sqrt{{a}}+\mathrm{1}\right)−{ln}\left(\mathrm{4}{a}−\mathrm{1}\right) \\ $$ $$\Rightarrow{f}\left({a}\right)=\mathrm{2}{ln}\left(\mathrm{2}\sqrt{{a}}+\mathrm{1}\right)−{ln}\left(\mathrm{4}{a}−\mathrm{1}\right) \\ $$ $$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}^{'} \left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\partial}{\partial{a}}\left(\frac{\mathrm{1}}{\sqrt{{x}^{\mathrm{2}} −{x}+{a}}}\right){dx} \\ $$ $$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\partial}{\partial{a}}\left\{\left(\:{x}^{\mathrm{2}} −{x}+{a}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \right\}{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\left({x}^{\mathrm{2}} −{x}+{a}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} {dx} \\ $$ $$=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} −{x}+{a}\right)\sqrt{{x}^{\mathrm{2}} −{x}+{a}}}\:{from}\:{another}\:{side} \\ $$ $${f}^{'} \left({a}\right)\:=\mathrm{2}\:\:×\frac{\frac{\mathrm{1}}{\sqrt{{a}}}}{\mathrm{2}\sqrt{{a}}+\mathrm{1}}−\frac{\mathrm{4}}{\mathrm{4}{a}−\mathrm{1}}\:=\mathrm{2}×\frac{\mathrm{1}}{\sqrt{{a}}\left(\mathrm{2}\sqrt{{a}}+\mathrm{1}\right)}−\frac{\mathrm{4}}{\mathrm{4}{a}−\mathrm{1}} \\ $$ $$=\frac{\mathrm{2}}{\mathrm{2}{a}+\sqrt{{a}}}−\frac{\mathrm{4}}{\mathrm{4}{a}−\mathrm{1}}\:\Rightarrow \\ $$ $$−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{\left({x}^{\mathrm{2}} −{x}+{a}\right)\sqrt{{x}^{\mathrm{2}} −{x}+{a}}}\:=\frac{\mathrm{2}}{\mathrm{2}{a}+\sqrt{{a}}}−\frac{\mathrm{4}}{\mathrm{4}{a}−\mathrm{1}}\:{also}\:{we}\:{get} \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} −{x}+{a}\right)\sqrt{{x}^{\mathrm{2}} −{x}+{a}}}\:=\frac{−\mathrm{4}}{\mathrm{2}{a}+\sqrt{{a}}}+\frac{\mathrm{8}}{\mathrm{4}{a}−\mathrm{1}} \\ $$
