Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 112449 by mathmax by abdo last updated on 07/Sep/20

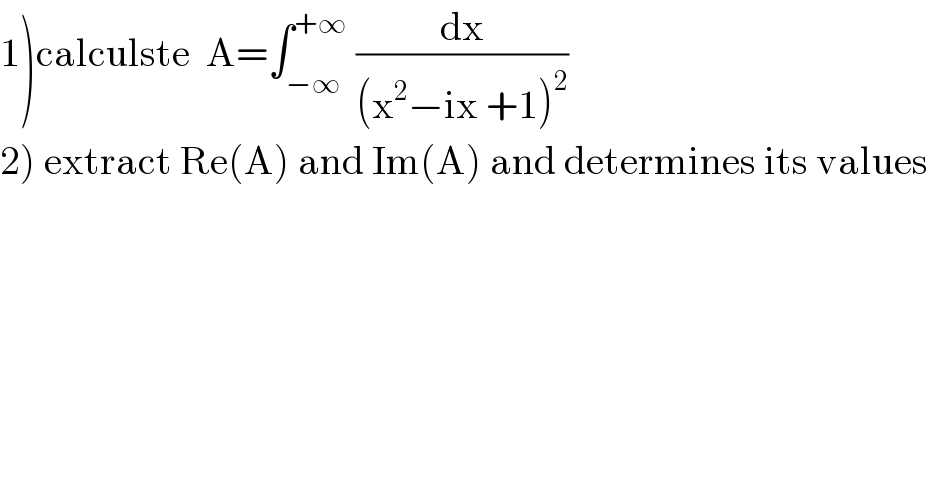
1)calculste A=∫_(−∞) ^(+∞) (dx/((x^2 −ix +1)^2 )) 2) extract Re(A) and Im(A) and determines its values

$$\left.\mathrm{1}\right)\mathrm{calculste}\:\:\mathrm{A}=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{ix}\:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{2}\right)\:\mathrm{extract}\:\mathrm{Re}\left(\mathrm{A}\right)\:\mathrm{and}\:\mathrm{Im}\left(\mathrm{A}\right)\:\mathrm{and}\:\mathrm{determines}\:\mathrm{its}\:\mathrm{values} \\ $$

Commented by MJS_new last updated on 08/Sep/20

I get A=((4π(√5))/(25)) can this be true?

$$\mathrm{I}\:\mathrm{get}\:{A}=\frac{\mathrm{4}\pi\sqrt{\mathrm{5}}}{\mathrm{25}}\:\mathrm{can}\:\mathrm{this}\:\mathrm{be}\:\mathrm{true}? \\ $$

Commented by MJS_new last updated on 08/Sep/20

Here's a better place to answer you. I'm well and I hope you're well, too. Nice to be in here again.

Commented by abdomsup last updated on 08/Sep/20

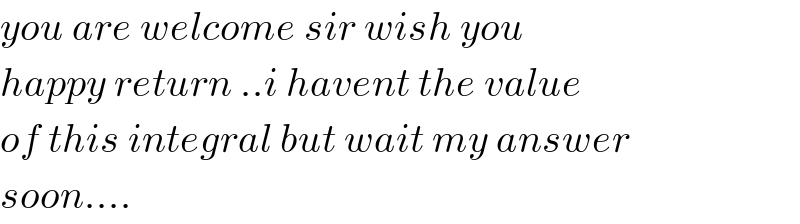
you are welcome sir wish you happy return ..i havent the value of this integral but wait my answer soon....

$${you}\:{are}\:{welcome}\:{sir}\:{wish}\:{you}\: \\ $$$${happy}\:{return}\:..{i}\:{havent}\:{the}\:{value} \\ $$$${of}\:{this}\:{integral}\:{but}\:{wait}\:{my}\:{answer} \\ $$$${soon}.... \\ $$

Answered by mathmax by abdo last updated on 08/Sep/20

1) A =∫_(−∞) ^(+∞) (dx/((x^2 −ix +1)^2 )) let ϕ(z) =(1/((z^2 −iz +1)^2 )) poles of ϕ? z^2 −iz +1 =0 →Δ =(−i)^2 −4 =−5 ⇒z_1 =((i+i(√5))/2) and z_2 =((i−i(√5))/2) ⇒ϕ(z) =(1/((z−z_1 )^2 (z−z_2 )^2 )) residus tbeorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,z_1 ) and Res(ϕ,z_1 ) =lim_(z→z_1 ) (1/((2−1)!)){(z−z_1 )^2 ϕ(z)}^((1)) =lim_(z→z_1 ) {(1/((z−z_2 )^2 ))}^((1)) =−lim_(z→z_1 ) ((2(z−z_2 ))/((z−z_2 )^4 )) =lim_(z→z_1 ) ((−2)/((z−z_2 )^3 )) =((−2)/((z_1 −z_2 )^3 )) =((−2)/((i(√5))^3 )) =((−2)/(−i5(√5))) =(2/(5i(√5))) ⇒ ∫_(−∞) ^(+∞) ϕ(z) dz =2iπ×(2/(5i(√5))) =((4π)/(5(√5))) ⇒★ A =((4π)/(5(√5)))★

$$\left.\mathrm{1}\right)\:\mathrm{A}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{ix}\:+\mathrm{1}\right)^{\mathrm{2}} }\:\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{z}^{\mathrm{2}} −\mathrm{iz}\:+\mathrm{1}\right)^{\mathrm{2}} }\:\:\mathrm{poles}\:\mathrm{of}\:\varphi? \\ $$$$\mathrm{z}^{\mathrm{2}} −\mathrm{iz}\:+\mathrm{1}\:=\mathrm{0}\:\rightarrow\Delta\:=\left(−\mathrm{i}\right)^{\mathrm{2}} −\mathrm{4}\:=−\mathrm{5}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{\mathrm{i}+\mathrm{i}\sqrt{\mathrm{5}}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\frac{\mathrm{i}−\mathrm{i}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)^{\mathrm{2}} \left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)^{\mathrm{2}} }\:\:\mathrm{residus}\:\mathrm{tbeorem}\:\mathrm{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{1}} \right)\:\:\mathrm{and}\: \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{1}} \right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{z}_{\mathrm{1}} } \:\:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)^{\mathrm{2}} \varphi\left(\mathrm{z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{z}_{\mathrm{1}} } \:\:\:\left\{\frac{\mathrm{1}}{\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \:=−\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{z}_{\mathrm{1}} } \:\:\:\:\frac{\mathrm{2}\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)}{\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)^{\mathrm{4}} } \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{z}_{\mathrm{1}} } \:\:\:\frac{−\mathrm{2}}{\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)^{\mathrm{3}} }\:=\frac{−\mathrm{2}}{\left(\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} \right)^{\mathrm{3}} }\:=\frac{−\mathrm{2}}{\left(\mathrm{i}\sqrt{\mathrm{5}}\right)^{\mathrm{3}} }\:=\frac{−\mathrm{2}}{−\mathrm{i5}\sqrt{\mathrm{5}}}\:=\frac{\mathrm{2}}{\mathrm{5i}\sqrt{\mathrm{5}}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\:\mathrm{dz}\:=\mathrm{2i}\pi×\frac{\mathrm{2}}{\mathrm{5i}\sqrt{\mathrm{5}}}\:=\frac{\mathrm{4}\pi}{\mathrm{5}\sqrt{\mathrm{5}}}\:\Rightarrow\bigstar\:\mathrm{A}\:=\frac{\mathrm{4}\pi}{\mathrm{5}\sqrt{\mathrm{5}}}\bigstar \\ $$

Answered by MJS_new last updated on 08/Sep/20

(1/((x^2 −ix+1)^2 ))= =((x^4 +x^2 +1)/((x^4 +3x^2 +1)^2 ))−((2x(x^2 +1))/((x^4 +3x^2 +1)^2 ))i ⇒ the imaginary part is uneven ⇒ ∫_(−a) ^(+a) (dx/((x^2 −ix+1)^2 ))=∫_(−a) ^(+a) ((x^4 +x^2 +1)/((x^4 +3x^2 +1)^2 ))dx ∫((x^4 +x^2 +1)/((x^4 +3x^2 +1)^2 ))dx= [Ostrogradski] =((x(2x^2 +3))/(5(x^4 +3x^2 +1)))+(2/5)∫((x^2 +1)/(x^4 +3x^2 +1))dx ∫((x^2 +1)/(x^4 +3x^2 +1))dx= =((5+(√5))/(10))∫(dx/(x^2 +((3+(√5))/2)))+((5−(√5))/(10))∫(dx/(x^2 +((3−(√5))/2)))= =((√5)/5)(−arctan (((1−(√5))x)/2) +arctan (((1+(√5))x)/2)) ⇒ ∫((x^4 +x^2 +1)/((x^4 +3x^2 +1)^2 ))dx= =((x(2x^2 +3))/(5(x^4 +3x^2 +1)))+((2(√5))/(25))(arctan (((1+(√5))x)/2) −arctan (((1−(√5))x)/2))+C ⇒ ∫_(−∞) ^(+∞) (dx/((x^2 −ix+1)^2 ))=∫_(−∞) ^(+∞) ((x^4 +x^2 +1)/((x^4 +3x^2 +1)^2 ))dx= =((4π(√5))/(25))

$$\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} −\mathrm{i}{x}+\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$=\frac{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{\left({x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{2}{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{\left({x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{i} \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{imaginary}\:\mathrm{part}\:\mathrm{is}\:\mathrm{uneven} \\ $$$$\Rightarrow\:\underset{−{a}} {\overset{+{a}} {\int}}\:\frac{{dx}}{\left({x}^{\mathrm{2}} −\mathrm{i}{x}+\mathrm{1}\right)^{\mathrm{2}} }=\underset{−{a}} {\overset{+{a}} {\int}}\:\frac{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{\left({x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\int\frac{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{\left({x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}\right] \\ $$$$=\frac{{x}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}\right)}{\mathrm{5}\left({x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{2}}{\mathrm{5}}\int\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$\int\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}}{dx}= \\ $$$$=\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{10}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{2}}}+\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{10}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{2}}}= \\ $$$$=\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}\left(−\mathrm{arctan}\:\frac{\left(\mathrm{1}−\sqrt{\mathrm{5}}\right){x}}{\mathrm{2}}\:+\mathrm{arctan}\:\frac{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right){x}}{\mathrm{2}}\right) \\ $$$$\Rightarrow \\ $$$$\int\frac{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{\left({x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}= \\ $$$$=\frac{{x}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}\right)}{\mathrm{5}\left({x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{25}}\left(\mathrm{arctan}\:\frac{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right){x}}{\mathrm{2}}\:−\mathrm{arctan}\:\frac{\left(\mathrm{1}−\sqrt{\mathrm{5}}\right){x}}{\mathrm{2}}\right)+{C} \\ $$$$\Rightarrow \\ $$$$\underset{−\infty} {\overset{+\infty} {\int}}\:\frac{{dx}}{\left({x}^{\mathrm{2}} −\mathrm{i}{x}+\mathrm{1}\right)^{\mathrm{2}} }=\underset{−\infty} {\overset{+\infty} {\int}}\frac{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{\left({x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}= \\ $$$$=\frac{\mathrm{4}\pi\sqrt{\mathrm{5}}}{\mathrm{25}} \\ $$

Commented by mathmax by abdo last updated on 08/Sep/20

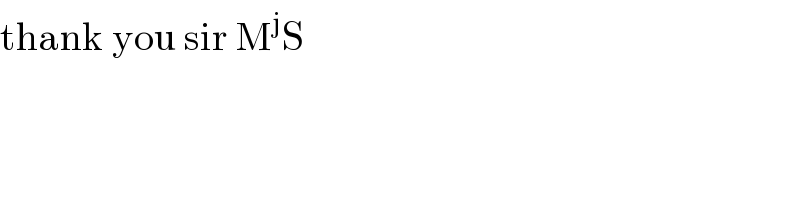
thank you sir M^j S

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{M}^{\mathrm{j}} \mathrm{S} \\ $$

Answered by mathmax by abdo last updated on 08/Sep/20

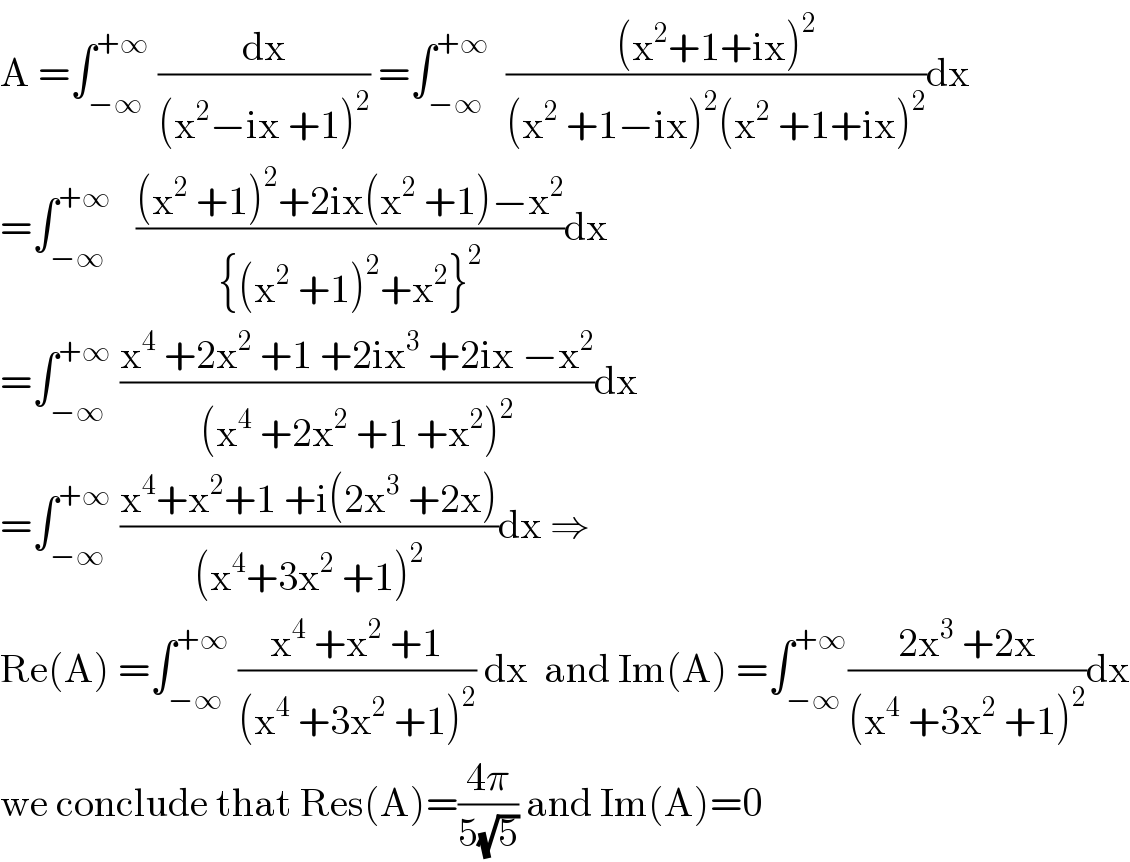
A =∫_(−∞) ^(+∞) (dx/((x^2 −ix +1)^2 )) =∫_(−∞) ^(+∞) (((x^2 +1+ix)^2 )/((x^2 +1−ix)^2 (x^2 +1+ix)^2 ))dx =∫_(−∞) ^(+∞) (((x^2 +1)^2 +2ix(x^2 +1)−x^2 )/({(x^2 +1)^2 +x^2 }^2 ))dx =∫_(−∞) ^(+∞) ((x^4 +2x^2 +1 +2ix^3 +2ix −x^2 )/((x^4 +2x^2 +1 +x^2 )^2 ))dx =∫_(−∞) ^(+∞) ((x^4 +x^2 +1 +i(2x^3 +2x))/((x^4 +3x^2 +1)^2 ))dx ⇒ Re(A) =∫_(−∞) ^(+∞) ((x^4 +x^2 +1)/((x^4 +3x^2 +1)^2 )) dx and Im(A) =∫_(−∞) ^(+∞) ((2x^3 +2x)/((x^4 +3x^2 +1)^2 ))dx we conclude that Res(A)=((4π)/(5(√5))) and Im(A)=0

$$\mathrm{A}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{ix}\:+\mathrm{1}\right)^{\mathrm{2}} }\:=\int_{−\infty} ^{+\infty} \:\:\frac{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}+\mathrm{ix}\right)^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{ix}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}+\mathrm{ix}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\int_{−\infty} ^{+\infty} \:\:\:\frac{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2ix}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)−\mathrm{x}^{\mathrm{2}} }{\left\{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \right\}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{x}^{\mathrm{4}} \:+\mathrm{2x}^{\mathrm{2}} \:+\mathrm{1}\:+\mathrm{2ix}^{\mathrm{3}} \:+\mathrm{2ix}\:−\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{4}} \:+\mathrm{2x}^{\mathrm{2}} \:+\mathrm{1}\:+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}\:+\mathrm{i}\left(\mathrm{2x}^{\mathrm{3}} \:+\mathrm{2x}\right)}{\left(\mathrm{x}^{\mathrm{4}} +\mathrm{3x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{Re}\left(\mathrm{A}\right)\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{x}^{\mathrm{4}} \:+\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}{\left(\mathrm{x}^{\mathrm{4}} \:+\mathrm{3x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{dx}\:\:\mathrm{and}\:\mathrm{Im}\left(\mathrm{A}\right)\:=\int_{−\infty} ^{+\infty} \frac{\mathrm{2x}^{\mathrm{3}} \:+\mathrm{2x}}{\left(\mathrm{x}^{\mathrm{4}} \:+\mathrm{3x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\mathrm{we}\:\mathrm{conclude}\:\mathrm{that}\:\mathrm{Res}\left(\mathrm{A}\right)=\frac{\mathrm{4}\pi}{\mathrm{5}\sqrt{\mathrm{5}}}\:\mathrm{and}\:\mathrm{Im}\left(\mathrm{A}\right)=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com