
Previous in Relation and Functions Next in Relation and Functions
Question Number 86983 by mathmax by abdo last updated on 01/Apr/20
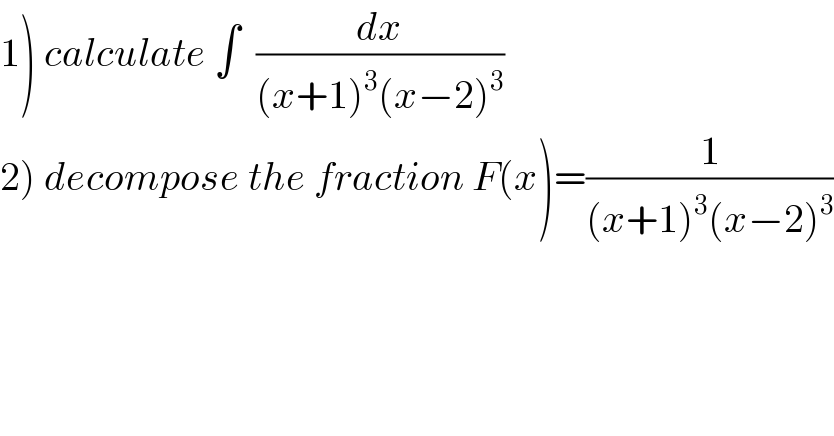
$$\left.\mathrm{1}\right)\:{calculate}\:\int\:\:\frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)^{\mathrm{3}} } \\ $$$$\left.\mathrm{2}\right)\:{decompose}\:{the}\:{fraction}\:{F}\left({x}\right)=\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)^{\mathrm{3}} } \\ $$
Commented by hknkrc46 last updated on 01/Apr/20
![(1/((x+1)^3 (x−2)^3 )) =(1/(27))∙(([(x+1)−(x−2)]^3 )/((x+1)^3 (x−2)^3 )) =(1/(27))[(((x+1)^3 −(x−2)^3 −3(x+1)(x−2)[(x+1)−(x−2)])/((x+1)^3 (x−2)^3 ))] =(1/(27))[(1/((x−2)^3 ))−(1/((x+1)^3 ))−(9/((x+1)^2 (x−2)^2 ))] =(1/(27))[(1/((x−2)^3 ))−(1/((x+1)^3 ))−(([(x+1)−(x−2)]^2 )/((x+1)^2 (x−2)^2 ))] =(1/(27))[(1/((x−2)^3 ))−(1/((x+1)^3 ))−(((x+1)^2 +(x−2)^2 −2(x+1)(x−2))/((x+1)^2 (x−2)^2 ))] =(1/(27))[(1/((x−2)^3 ))−(1/((x+1)^3 ))−(1/((x−2)^2 ))−(1/((x+1)^2 ))+(2/((x+1)(x−2)))] =(1/(27))[(1/((x−2)^3 ))−(1/((x+1)^3 ))−(1/((x−2)^2 ))−(1/((x+1)^2 ))+(2/3)∙(((x+1)−(x−2))/((x+1)(x−2)))] =(1/(27))[(1/((x−2)^3 ))−(1/((x+1)^3 ))−(1/((x−2)^2 ))−(1/((x+1)^2 ))+(2/3)∙((1/(x−2))−(1/(x+1)))] =(1/(27))[(1/((x−2)^3 ))−(1/((x+1)^3 ))−(1/((x−2)^2 ))−(1/((x+1)^2 ))]+(2/(81))∙((1/(x−2))−(1/(x+1))) ∫ (dx/((x+1)^3 (x−2)^3 ))=(1/(27))[(((x−2)^(−2) )/(−2))+(((x+1)^(−2) )/2)+(x−2)^(−1) +(x+1)^(−1) ]+(2/(81))ln(((x−2)/(x+1)))+c](Q86988.png)
$$\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)^{\mathrm{3}} }\:=\frac{\mathrm{1}}{\mathrm{27}}\centerdot\frac{\left[\left({x}+\mathrm{1}\right)−\left({x}−\mathrm{2}\right)\right]^{\mathrm{3}} }{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{27}}\left[\frac{\left({x}+\mathrm{1}\right)^{\mathrm{3}} −\left({x}−\mathrm{2}\right)^{\mathrm{3}} −\mathrm{3}\left({x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left[\left({x}+\mathrm{1}\right)−\left({x}−\mathrm{2}\right)\right]}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)^{\mathrm{3}} }\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{27}}\left[\frac{\mathrm{1}}{\left({x}−\mathrm{2}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} }−\frac{\mathrm{9}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} \left({x}−\mathrm{2}\right)^{\mathrm{2}} }\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{27}}\left[\frac{\mathrm{1}}{\left({x}−\mathrm{2}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} }−\frac{\left[\left({x}+\mathrm{1}\right)−\left({x}−\mathrm{2}\right)\right]^{\mathrm{2}} }{\left({x}+\mathrm{1}\right)^{\mathrm{2}} \left({x}−\mathrm{2}\right)^{\mathrm{2}} }\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{27}}\left[\frac{\mathrm{1}}{\left({x}−\mathrm{2}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} }−\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\left({x}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}\left({x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} \left({x}−\mathrm{2}\right)^{\mathrm{2}} }\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{27}}\left[\frac{\mathrm{1}}{\left({x}−\mathrm{2}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{2}}{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{27}}\left[\frac{\mathrm{1}}{\left({x}−\mathrm{2}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{3}}\centerdot\frac{\left({x}+\mathrm{1}\right)−\left({x}−\mathrm{2}\right)}{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{27}}\left[\frac{\mathrm{1}}{\left({x}−\mathrm{2}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{3}}\centerdot\left(\frac{\mathrm{1}}{{x}−\mathrm{2}}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{27}}\left[\frac{\mathrm{1}}{\left({x}−\mathrm{2}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\right]+\frac{\mathrm{2}}{\mathrm{81}}\centerdot\left(\frac{\mathrm{1}}{{x}−\mathrm{2}}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right) \\ $$$$\int\:\:\frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{27}}\left[\frac{\left({x}−\mathrm{2}\right)^{−\mathrm{2}} }{−\mathrm{2}}+\frac{\left({x}+\mathrm{1}\right)^{−\mathrm{2}} }{\mathrm{2}}+\left({x}−\mathrm{2}\right)^{−\mathrm{1}} +\left({x}+\mathrm{1}\right)^{−\mathrm{1}} \right]+\frac{\mathrm{2}}{\mathrm{81}}{ln}\left(\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}\right)+{c} \\ $$
Commented by mathmax by abdo last updated on 01/Apr/20
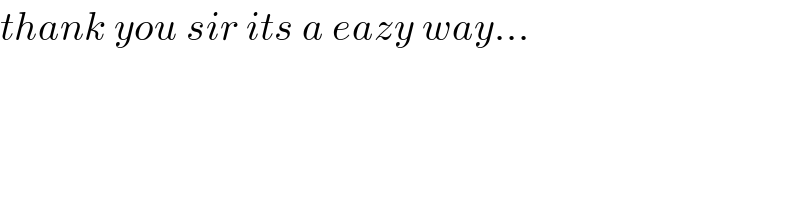
$${thank}\:{you}\:{sir}\:{its}\:{a}\:{eazy}\:{way}... \\ $$
Commented by mathmax by abdo last updated on 01/Apr/20

$$\left.\mathrm{1}\right)\:{I}\:=\int\:\:\frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)^{\mathrm{3}} }\:\Rightarrow\:{I}\:=\int\:\:\:\frac{{dx}}{\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{2}}\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)^{\mathrm{6}} }\:{changement} \\ $$$$\frac{{x}+\mathrm{1}}{{x}−\mathrm{2}}\:={t}\:{give}\:{x}+\mathrm{1}\:={tx}−\mathrm{2}{t}\:\Rightarrow\left(\mathrm{1}−{t}\right){x}\:=−\mathrm{1}−\mathrm{2}{t}\:\Rightarrow{x}\:=\frac{\mathrm{2}{t}+\mathrm{1}}{{t}−\mathrm{1}}\:\Rightarrow \\ $$$$\frac{{dx}}{{dt}}\:=\frac{\mathrm{2}\left({t}−\mathrm{1}\right)−\left(\mathrm{2}{t}+\mathrm{1}\right)}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{−\mathrm{3}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }\:{also}\:{x}−\mathrm{2}\:=\frac{\mathrm{2}{t}+\mathrm{1}}{{t}−\mathrm{1}}−\mathrm{2}=\frac{\mathrm{2}{t}+\mathrm{1}−\mathrm{2}{t}+\mathrm{2}}{{t}−\mathrm{1}} \\ $$$$=\frac{\mathrm{3}}{{t}−\mathrm{1}}\:\Rightarrow\:{I}\:=\:\int\:\:\frac{−\mathrm{3}{dt}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} {t}^{\mathrm{3}} \left(\frac{\mathrm{3}}{{t}−\mathrm{1}}\right)^{\mathrm{6}} }\:=−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{5}} }\:\int\:\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{4}} \:{dt}}{{t}^{\mathrm{3}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{5}} }\int\:\:\frac{\sum_{{k}=\mathrm{0}} ^{\mathrm{4}} \:{C}_{\mathrm{4}} ^{{k}} \:{t}^{{k}} \left(−\mathrm{1}\right)^{\mathrm{4}−{k}} }{{t}^{\mathrm{3}} }{dt}\:=−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{5}} }\:\sum_{{k}=\mathrm{0}} ^{\mathrm{4}} \:\left(−\mathrm{1}\right)^{{k}} \:{C}_{\mathrm{4}} ^{{k}} \int\:{t}^{{k}−\mathrm{3}} \:{dt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{5}} }\sum_{{k}=\mathrm{0}\:{and}\:{k}\neq\mathrm{2}} ^{\mathrm{4}} \:\left(−\mathrm{1}\right)^{{k}} \:{C}_{\mathrm{4}} ^{{k}} \:\frac{\mathrm{1}}{{k}−\mathrm{2}}{t}^{{k}−\mathrm{2}} \:\:\:−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{5}} }\:{C}_{\mathrm{4}} ^{\mathrm{2}} \:{ln}\mid{t}\mid\:+{C} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{5}} }\:\sum_{{k}=\mathrm{0}\:{and}\:{k}\neq\mathrm{2}} ^{\mathrm{4}} \:\frac{\left(−\mathrm{1}\right)^{{k}} \:{C}_{\mathrm{4}} ^{{k}} }{{k}−\mathrm{2}}\:\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{2}}\right)^{{k}−\mathrm{2}} \:−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{5}} }\:{C}_{\mathrm{4}} ^{\mathrm{2}} \:{ln}\mid\frac{{x}+\mathrm{1}}{{x}−\mathrm{2}}\mid\:+{C} \\ $$$$−\mathrm{3}^{\mathrm{5}} {I}\:=\frac{{C}_{\mathrm{4}} ^{\mathrm{0}} }{−\mathrm{2}}\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{2}}\right)^{−\mathrm{2}} +\frac{{C}_{\mathrm{4}} ^{\mathrm{1}} }{\mathrm{1}}\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{2}}\right)^{−\mathrm{1}} −{C}_{\mathrm{4}} ^{\mathrm{3}} \:\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{2}}\right)\:+\frac{{C}_{\mathrm{4}} ^{\mathrm{4}} }{\mathrm{2}}\left(\frac{{x}+\mathrm{1}}{{x}−\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$+\:{C}_{\mathrm{4}} ^{\mathrm{2}} {ln}\mid\frac{{x}+\mathrm{1}}{{x}−\mathrm{2}}\mid\:+{C} \\ $$
Commented by mathmax by abdo last updated on 01/Apr/20
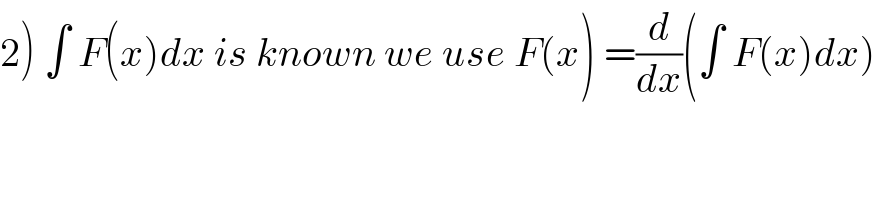
$$\left.\mathrm{2}\right)\:\int\:{F}\left({x}\right){dx}\:{is}\:{known}\:{we}\:{use}\:{F}\left({x}\right)\:=\frac{{d}}{{dx}}\left(\int\:{F}\left({x}\right){dx}\right) \\ $$
Answered by mind is power last updated on 02/Apr/20
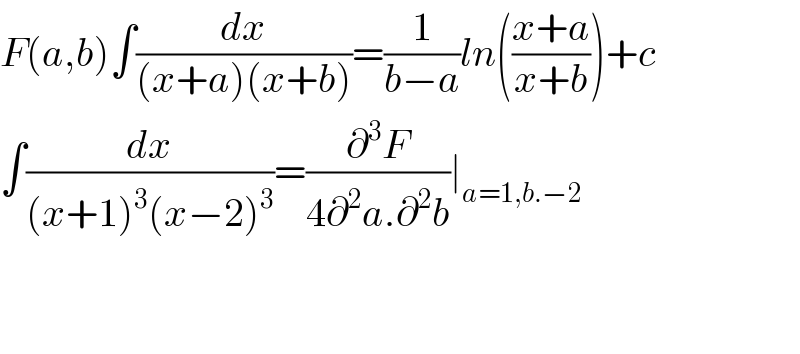
$${F}\left({a},{b}\right)\int\frac{{dx}}{\left({x}+{a}\right)\left({x}+{b}\right)}=\frac{\mathrm{1}}{{b}−{a}}{ln}\left(\frac{{x}+{a}}{{x}+{b}}\right)+{c} \\ $$$$\int\frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}−\mathrm{2}\right)^{\mathrm{3}} }=\frac{\partial^{\mathrm{3}} {F}}{\mathrm{4}\partial^{\mathrm{2}} {a}.\partial^{\mathrm{2}} {b}}\mid_{{a}=\mathrm{1},{b}.−\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$
