
Question Number 81427 by abdomathmax last updated on 13/Feb/20
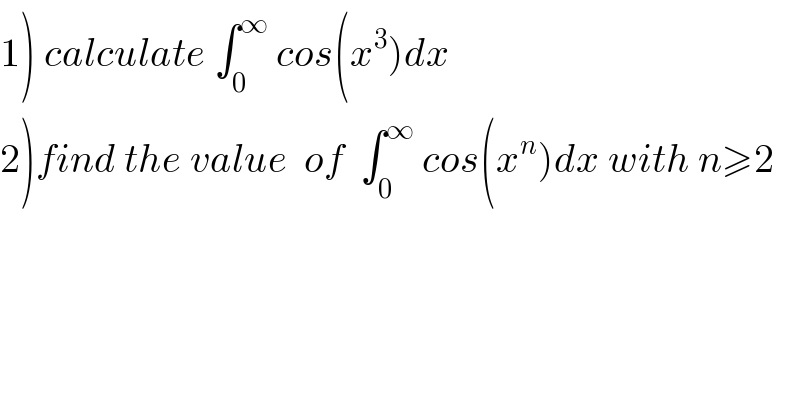
$$\left.\mathrm{1}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\infty} \:{cos}\left({x}^{\mathrm{3}} \right){dx} \\ $$$$\left.\mathrm{2}\right){find}\:{the}\:{value}\:\:{of}\:\:\int_{\mathrm{0}} ^{\infty} \:{cos}\left({x}^{{n}} \right){dx}\:{with}\:{n}\geqslant\mathrm{2} \\ $$
Commented by mind is power last updated on 13/Feb/20
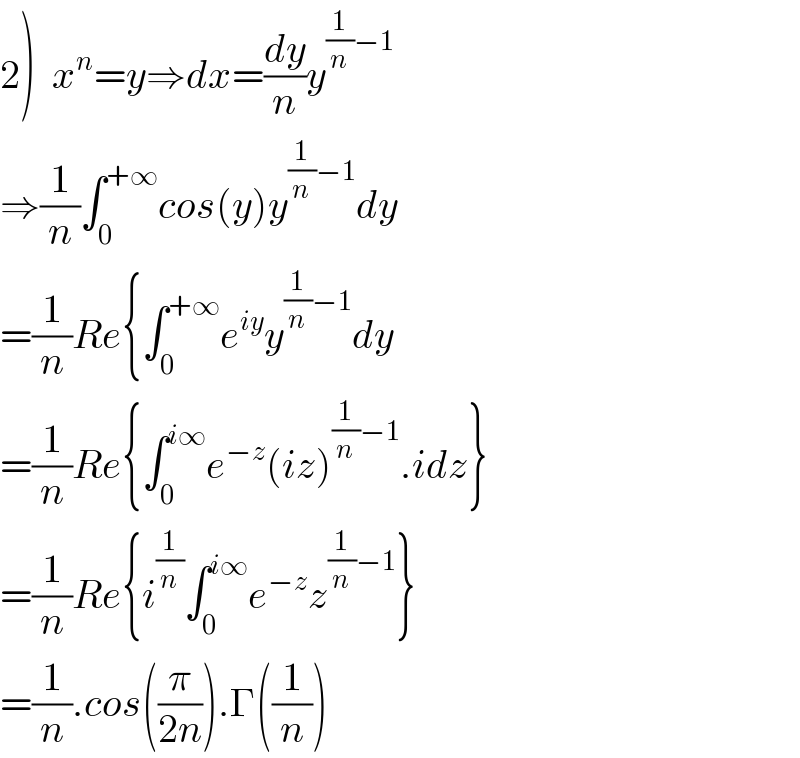
$$\left.\mathrm{2}\right)\:\:{x}^{{n}} ={y}\Rightarrow{dx}=\frac{{dy}}{{n}}{y}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{+\infty} {cos}\left({y}\right){y}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} {dy} \\ $$$$=\frac{\mathrm{1}}{{n}}{Re}\left\{\int_{\mathrm{0}} ^{+\infty} {e}^{{iy}} {y}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} {dy}\right. \\ $$$$=\frac{\mathrm{1}}{{n}}{Re}\left\{\int_{\mathrm{0}} ^{{i}\infty} {e}^{−{z}} \left({iz}\right)^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} .{idz}\right\} \\ $$$$=\frac{\mathrm{1}}{{n}}{Re}\left\{{i}^{\frac{\mathrm{1}}{{n}}} \int_{\mathrm{0}} ^{{i}\infty} {e}^{−{z}} {z}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} \right\} \\ $$$$=\frac{\mathrm{1}}{{n}}.{cos}\left(\frac{\pi}{\mathrm{2}{n}}\right).\Gamma\left(\frac{\mathrm{1}}{{n}}\right) \\ $$
Commented by abdomathmax last updated on 13/Feb/20

$${thank}\:{you}\:{sir}. \\ $$
Commented by abdomathmax last updated on 13/Feb/20
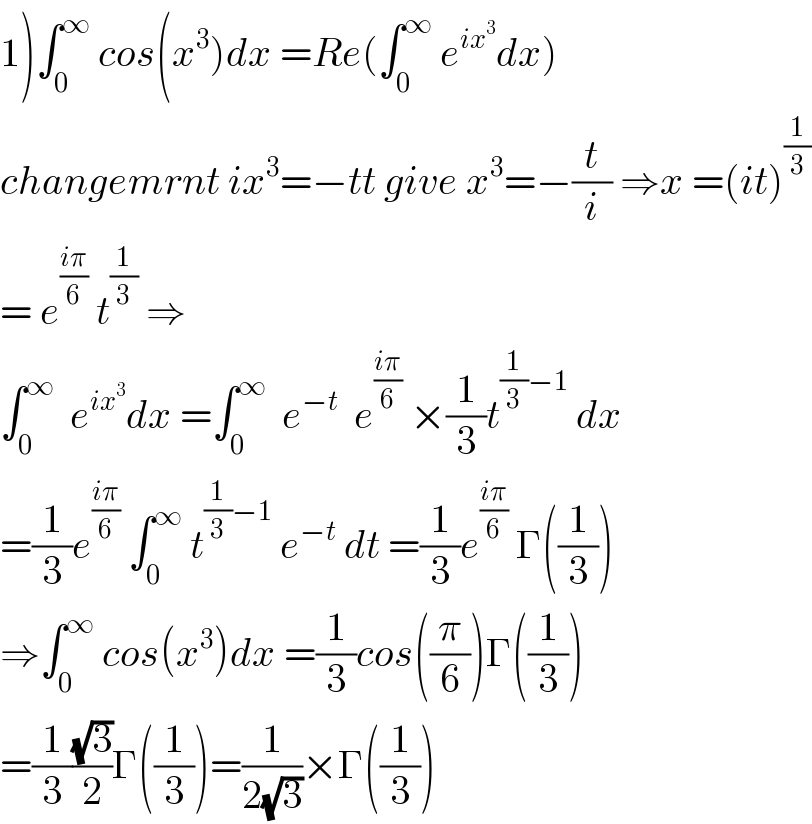
$$\left.\mathrm{1}\right)\int_{\mathrm{0}} ^{\infty} \:{cos}\left({x}^{\mathrm{3}} \right){dx}\:={Re}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{{ix}^{\mathrm{3}} } {dx}\right) \\ $$$${changemrnt}\:{ix}^{\mathrm{3}} =−{tt}\:{give}\:{x}^{\mathrm{3}} =−\frac{{t}}{{i}}\:\Rightarrow{x}\:=\left({it}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$=\:{e}^{\frac{{i}\pi}{\mathrm{6}}} \:{t}^{\frac{\mathrm{1}}{\mathrm{3}}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{{ix}^{\mathrm{3}} } {dx}\:=\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{t}} \:\:{e}^{\frac{{i}\pi}{\mathrm{6}}} \:×\frac{\mathrm{1}}{\mathrm{3}}{t}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} \:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{e}^{\frac{{i}\pi}{\mathrm{6}}} \:\int_{\mathrm{0}} ^{\infty} \:{t}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} \:{e}^{−{t}} \:{dt}\:=\frac{\mathrm{1}}{\mathrm{3}}{e}^{\frac{{i}\pi}{\mathrm{6}}} \:\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \:{cos}\left({x}^{\mathrm{3}} \right){dx}\:=\frac{\mathrm{1}}{\mathrm{3}}{cos}\left(\frac{\pi}{\mathrm{6}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}×\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$
Commented by abdomathmax last updated on 13/Feb/20
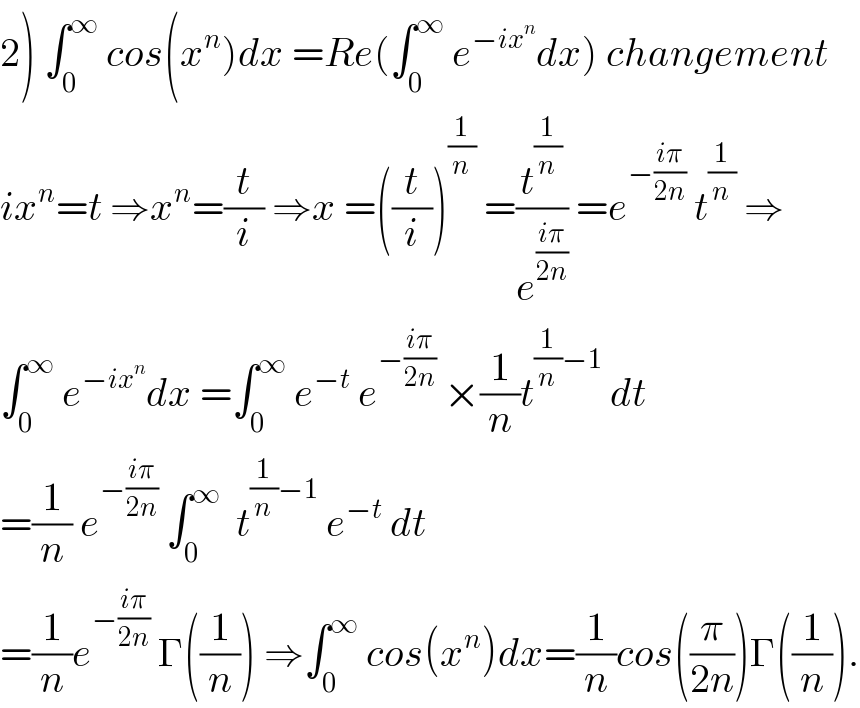
$$\left.\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\infty} \:{cos}\left({x}^{{n}} \right){dx}\:={Re}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{−{ix}^{{n}} } {dx}\right)\:{changement} \\ $$$${ix}^{{n}} ={t}\:\Rightarrow{x}^{{n}} =\frac{{t}}{{i}}\:\Rightarrow{x}\:=\left(\frac{{t}}{{i}}\right)^{\frac{\mathrm{1}}{{n}}} \:=\frac{{t}^{\frac{\mathrm{1}}{{n}}} }{{e}^{\frac{{i}\pi}{\mathrm{2}{n}}} }\:={e}^{−\frac{{i}\pi}{\mathrm{2}{n}}} \:{t}^{\frac{\mathrm{1}}{{n}}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{−{ix}^{{n}} } {dx}\:=\int_{\mathrm{0}} ^{\infty} \:{e}^{−{t}} \:{e}^{−\frac{{i}\pi}{\mathrm{2}{n}}} \:×\frac{\mathrm{1}}{{n}}{t}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{{n}}\:{e}^{−\frac{{i}\pi}{\mathrm{2}{n}}} \:\int_{\mathrm{0}} ^{\infty} \:\:{t}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} \:{e}^{−{t}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{{n}}{e}^{−\frac{{i}\pi}{\mathrm{2}{n}}} \:\Gamma\left(\frac{\mathrm{1}}{{n}}\right)\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:{cos}\left({x}^{{n}} \right){dx}=\frac{\mathrm{1}}{{n}}{cos}\left(\frac{\pi}{\mathrm{2}{n}}\right)\Gamma\left(\frac{\mathrm{1}}{{n}}\right). \\ $$
Answered by mind is power last updated on 13/Feb/20
![1) u=x^3 ⇒∫_0 ^(+∞) (1/3)((cos(u))/u^(2/3) )du =∫_0 ^(+∞) ((cos(u))/u^(2/3) )du =Re∫_0 ^(+∞) e^(iu) u^(−(2/3)) du −y=iu⇒ du=idy Re{i^(1/3) ∫_0 ^(i∞) e^(−y) y^(−(2/3)) dy} Re{e^((iπ)/6) ∫_0 ^(i∞) e^(−y) y^(−(2/3)) dy} ∫_r ^R e^(−y) y^(−(2/3)) dy+∫_(Re^(iθ) ) e^(−y) y^(−(2/3)) dy+∫_(iR) ^(ir) e^(−y) y^(−(2/3)) dy+∫_C_r e^(−y) y^(−(2/3)) dy C_r =re^(it) ,t∈[((π�)/2) ,0] r→0 ∫_C_R e^(−y) y^(−(2/3)) dy=0 R→∞ ∫c_r e^(−y) y^(−((2.)/3)) dy→0 ⇒∫_(iR) ^(ir) e^(−y) y^(−(2/3)) dy=−∫_r ^R e^(−y) y^(−(2/3)) dy ⇔∫_0 ^(i∞) e^(−y) y^(−(2/3)) dy=∫_0 ^(+∞) e^(−y) y^(−(2/3)) dy=Γ((1/3)) ⇒∫_0 ^(+∞) cos(x^3 )dx=(1/3)Γ((1/3))cos((π/6))=((√3)/6).Γ((1/3))](Q81477.png)
$$\left.\mathrm{1}\right) \\ $$$${u}={x}^{\mathrm{3}} \Rightarrow\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{1}}{\mathrm{3}}\frac{{cos}\left({u}\right)}{{u}^{\frac{\mathrm{2}}{\mathrm{3}}} }{du} \\ $$$$=\int_{\mathrm{0}} ^{+\infty} \frac{{cos}\left({u}\right)}{{u}^{\frac{\mathrm{2}}{\mathrm{3}}} }{du} \\ $$$$={Re}\int_{\mathrm{0}} ^{+\infty} {e}^{{iu}} {u}^{−\frac{\mathrm{2}}{\mathrm{3}}} {du} \\ $$$$−{y}={iu}\Rightarrow \\ $$$${du}={idy} \\ $$$${Re}\left\{{i}^{\frac{\mathrm{1}}{\mathrm{3}}} \int_{\mathrm{0}} ^{{i}\infty} {e}^{−{y}} {y}^{−\frac{\mathrm{2}}{\mathrm{3}}} {dy}\right\} \\ $$$${Re}\left\{{e}^{\frac{{i}\pi}{\mathrm{6}}} \int_{\mathrm{0}} ^{{i}\infty} {e}^{−{y}} \:\:{y}^{−\frac{\mathrm{2}}{\mathrm{3}}} {dy}\right\} \\ $$$$\int_{{r}} ^{{R}} {e}^{−{y}} {y}^{−\frac{\mathrm{2}}{\mathrm{3}}} {dy}+\int_{{Re}^{{i}\theta} } {e}^{−{y}} {y}^{−\frac{\mathrm{2}}{\mathrm{3}}} {dy}+\int_{{iR}} ^{{ir}} {e}^{−{y}} {y}^{−\frac{\mathrm{2}}{\mathrm{3}}} {dy}+\int_{{C}_{{r}} } {e}^{−{y}} {y}^{−\frac{\mathrm{2}}{\mathrm{3}}} {dy} \\ $$$${C}_{{r}} \:\:={re}^{{it}} ,{t}\in\left[\frac{\pi�}{\mathrm{2}}\:\:,\mathrm{0}\right]\:\:{r}\rightarrow\mathrm{0} \\ $$$$\int_{{C}_{{R}} } {e}^{−{y}} {y}^{−\frac{\mathrm{2}}{\mathrm{3}}} {dy}=\mathrm{0}\:\:{R}\rightarrow\infty \\ $$$$\int{c}_{{r}} \:\:\:\:{e}^{−{y}} {y}^{−\frac{\mathrm{2}.}{\mathrm{3}}} {dy}\rightarrow\mathrm{0} \\ $$$$\Rightarrow\int_{{iR}} ^{{ir}} {e}^{−{y}} {y}^{−\frac{\mathrm{2}}{\mathrm{3}}} {dy}=−\int_{{r}} ^{{R}} {e}^{−{y}} {y}^{−\frac{\mathrm{2}}{\mathrm{3}}} {dy} \\ $$$$\Leftrightarrow\int_{\mathrm{0}} ^{{i}\infty} {e}^{−{y}} {y}^{−\frac{\mathrm{2}}{\mathrm{3}}} {dy}=\int_{\mathrm{0}} ^{+\infty} {e}^{−{y}} {y}^{−\frac{\mathrm{2}}{\mathrm{3}}} {dy}=\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{+\infty} {cos}\left({x}^{\mathrm{3}} \right){dx}=\frac{\mathrm{1}}{\mathrm{3}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right){cos}\left(\frac{\pi}{\mathrm{6}}\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}.\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$ \\ $$
