
Question Number 125146 by mathmax by abdo last updated on 08/Dec/20
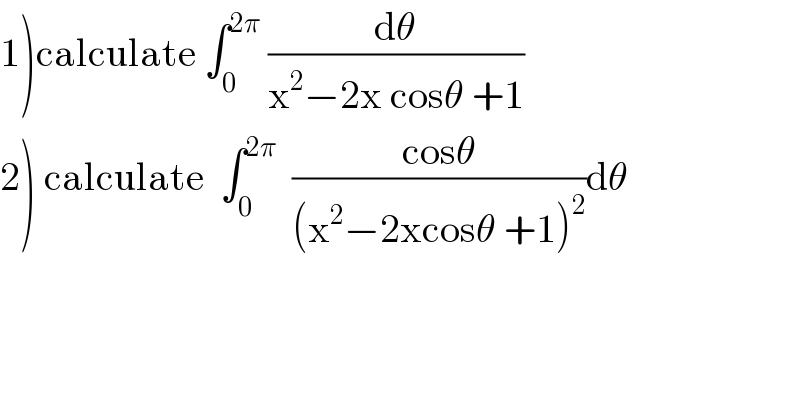
$$\left.\mathrm{1}\right)\mathrm{calculate}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{d}\theta}{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}\:\mathrm{cos}\theta\:+\mathrm{1}} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{\mathrm{cos}\theta}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2xcos}\theta\:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{d}\theta \\ $$
Answered by Dwaipayan Shikari last updated on 08/Dec/20
![x^2 −2xcos𝛉+1=0 x=cos𝛉±isin𝛉=e^(±i𝛉) ∫_0 ^(2π) (1/((x−e^(iθ) )(x−e^(−iθ) )))dx =∫_0 ^(2π) (1/(x−e^(iθ) ))−(1/(x−e^(−iθ) ))dx=(1/(2cosθ))∫_0 ^(2π) (1/((x−e^(iθ) )))−(1/((x−e^(−iθ) ))) =(1/(2cosθ))[log(((x−e^(iθ) )/(x−e^(−iθ) )))]_0 ^(2π) =(( 1)/(2cosθ))log(((2π−e^(iθ) )/(2π−e^(−iθ) )))−((θi)/(cosθ))](Q125160.png)
$${x}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{xcos}\theta}+\mathrm{1}=\mathrm{0} \\ $$$${x}=\boldsymbol{{cos}\theta}\pm\boldsymbol{{isin}\theta}=\boldsymbol{{e}}^{\pm\boldsymbol{{i}\theta}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\mathrm{1}}{\left({x}−{e}^{{i}\theta} \right)\left({x}−{e}^{−{i}\theta} \right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\mathrm{1}}{{x}−{e}^{{i}\theta} }−\frac{\mathrm{1}}{{x}−{e}^{−{i}\theta} }{dx}=\frac{\mathrm{1}}{\mathrm{2}{cos}\theta}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\mathrm{1}}{\left({x}−{e}^{{i}\theta} \right)}−\frac{\mathrm{1}}{\left({x}−{e}^{−{i}\theta} \right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{cos}\theta}\left[{log}\left(\frac{{x}−{e}^{{i}\theta} }{{x}−{e}^{−{i}\theta} }\right)\right]_{\mathrm{0}} ^{\mathrm{2}\pi} =\frac{\:\mathrm{1}}{\mathrm{2}{cos}\theta}{log}\left(\frac{\mathrm{2}\pi−{e}^{{i}\theta} }{\mathrm{2}\pi−{e}^{−{i}\theta} }\right)−\frac{\theta{i}}{{cos}\theta} \\ $$
Answered by mathmax by abdo last updated on 08/Dec/20

$$\left.\mathrm{2}\right)\:\mathrm{we}\:\mathrm{have}\:\mathrm{I}\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{d}\theta}{\mathrm{x}^{\mathrm{2}} −\mathrm{2xcos}\theta\:+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{I}^{'} \left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\partial}{\partial\mathrm{x}}\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2xcos}\theta\:+\mathrm{1}}\right)\mathrm{d}\theta\:=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2x}−\mathrm{2cos}\theta}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2xcos}\theta\:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{d}\theta \\ $$$$=−\mathrm{2x}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{d}\theta}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2xcos}\theta\:+\mathrm{1}\right)^{\mathrm{2}} }\:+\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\theta}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2xcos}\theta+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{d}\theta\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{cos}\theta\:\mathrm{d}\theta}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2xcos}\theta\:+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\mathrm{I}^{'} \left(\mathrm{x}\right)+\mathrm{2x}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{d}\theta}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2xcos}\theta+\mathrm{1}\right)^{\mathrm{2}} }\right\} \\ $$$$\mathrm{I}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{known}\:\mathrm{rest}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{I}^{'} \left(\mathrm{x}\right)\:\mathrm{and}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{d}\theta}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2xcos}\theta\:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$...\mathrm{be}\:\mathrm{continued}.. \\ $$
Answered by mathmax by abdo last updated on 08/Dec/20
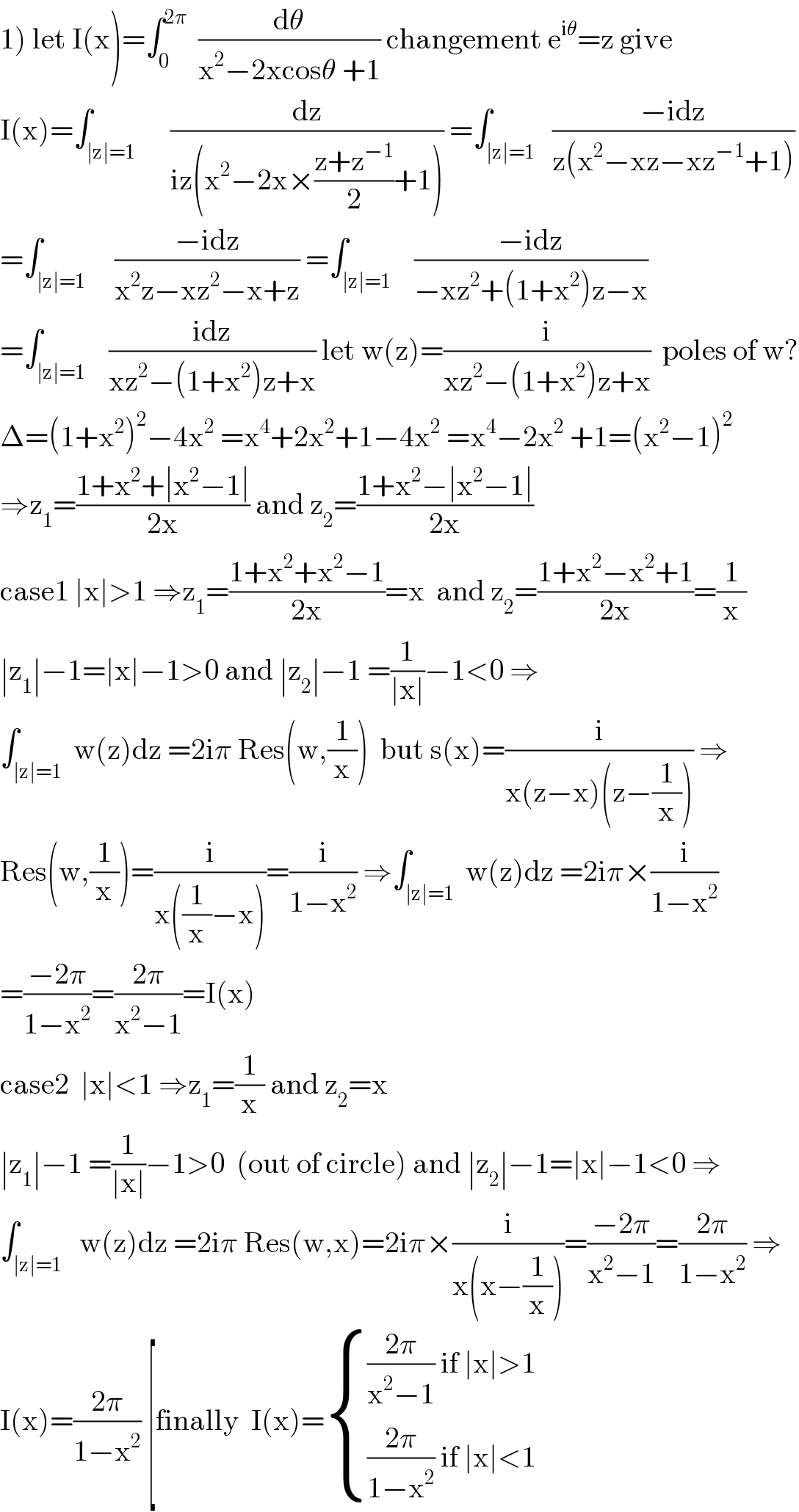
$$\left.\mathrm{1}\right)\:\mathrm{let}\:\mathrm{I}\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{\mathrm{d}\theta}{\mathrm{x}^{\mathrm{2}} −\mathrm{2xcos}\theta\:+\mathrm{1}}\:\mathrm{changement}\:\mathrm{e}^{\mathrm{i}\theta} =\mathrm{z}\:\mathrm{give} \\ $$$$\mathrm{I}\left(\mathrm{x}\right)=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\:\:\frac{\mathrm{dz}}{\mathrm{iz}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}×\frac{\mathrm{z}+\mathrm{z}^{−\mathrm{1}} }{\mathrm{2}}+\mathrm{1}\right)}\:=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\frac{−\mathrm{idz}}{\mathrm{z}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{xz}−\mathrm{xz}^{−\mathrm{1}} +\mathrm{1}\right)} \\ $$$$=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\:\frac{−\mathrm{idz}}{\mathrm{x}^{\mathrm{2}} \mathrm{z}−\mathrm{xz}^{\mathrm{2}} −\mathrm{x}+\mathrm{z}}\:=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\frac{−\mathrm{idz}}{−\mathrm{xz}^{\mathrm{2}} +\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{z}−\mathrm{x}} \\ $$$$=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\frac{\mathrm{idz}}{\mathrm{xz}^{\mathrm{2}} −\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{z}+\mathrm{x}}\:\mathrm{let}\:\mathrm{w}\left(\mathrm{z}\right)=\frac{\mathrm{i}}{\mathrm{xz}^{\mathrm{2}} −\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{z}+\mathrm{x}}\:\:\mathrm{poles}\:\mathrm{of}\:\mathrm{w}? \\ $$$$\Delta=\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4x}^{\mathrm{2}} \:=\mathrm{x}^{\mathrm{4}} +\mathrm{2x}^{\mathrm{2}} +\mathrm{1}−\mathrm{4x}^{\mathrm{2}} \:=\mathrm{x}^{\mathrm{4}} −\mathrm{2x}^{\mathrm{2}} \:+\mathrm{1}=\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{\mathrm{1}+\mathrm{x}^{\mathrm{2}} +\mid\mathrm{x}^{\mathrm{2}} −\mathrm{1}\mid}{\mathrm{2x}}\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\frac{\mathrm{1}+\mathrm{x}^{\mathrm{2}} −\mid\mathrm{x}^{\mathrm{2}} −\mathrm{1}\mid}{\mathrm{2x}} \\ $$$$\mathrm{case1}\:\mid\mathrm{x}\mid>\mathrm{1}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{\mathrm{1}+\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2x}}=\mathrm{x}\:\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\frac{\mathrm{1}+\mathrm{x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2x}}=\frac{\mathrm{1}}{\mathrm{x}} \\ $$$$\mid\mathrm{z}_{\mathrm{1}} \mid−\mathrm{1}=\mid\mathrm{x}\mid−\mathrm{1}>\mathrm{0}\:\mathrm{and}\:\mid\mathrm{z}_{\mathrm{2}} \mid−\mathrm{1}\:=\frac{\mathrm{1}}{\mid\mathrm{x}\mid}−\mathrm{1}<\mathrm{0}\:\Rightarrow \\ $$$$\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\mathrm{w}\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\mathrm{w},\frac{\mathrm{1}}{\mathrm{x}}\right)\:\:\mathrm{but}\:\mathrm{s}\left(\mathrm{x}\right)=\frac{\mathrm{i}}{\mathrm{x}\left(\mathrm{z}−\mathrm{x}\right)\left(\mathrm{z}−\frac{\mathrm{1}}{\mathrm{x}}\right)}\:\Rightarrow \\ $$$$\mathrm{Res}\left(\mathrm{w},\frac{\mathrm{1}}{\mathrm{x}}\right)=\frac{\mathrm{i}}{\mathrm{x}\left(\frac{\mathrm{1}}{\mathrm{x}}−\mathrm{x}\right)}=\frac{\mathrm{i}}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\Rightarrow\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\mathrm{w}\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi×\frac{\mathrm{i}}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{2}\pi}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }=\frac{\mathrm{2}\pi}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}=\mathrm{I}\left(\mathrm{x}\right) \\ $$$$\mathrm{case2}\:\:\mid\mathrm{x}\mid<\mathrm{1}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{x}}\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\mathrm{x} \\ $$$$\mid\mathrm{z}_{\mathrm{1}} \mid−\mathrm{1}\:=\frac{\mathrm{1}}{\mid\mathrm{x}\mid}−\mathrm{1}>\mathrm{0}\:\:\left(\mathrm{out}\:\mathrm{of}\:\mathrm{circle}\right)\:\mathrm{and}\:\mid\mathrm{z}_{\mathrm{2}} \mid−\mathrm{1}=\mid\mathrm{x}\mid−\mathrm{1}<\mathrm{0}\:\Rightarrow \\ $$$$\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\mathrm{w}\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\mathrm{w},\mathrm{x}\right)=\mathrm{2i}\pi×\frac{\mathrm{i}}{\mathrm{x}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)}=\frac{−\mathrm{2}\pi}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{2}\pi}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{I}\left(\mathrm{x}\right)=\frac{\mathrm{2}\pi}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\left[\mathrm{finally}\:\:\mathrm{I}\left(\mathrm{x}\right)=\begin{cases}{\frac{\mathrm{2}\pi}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:\mathrm{if}\:\mid\mathrm{x}\mid>\mathrm{1}}\\{\frac{\mathrm{2}\pi}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\mathrm{if}\:\mid\mathrm{x}\mid<\mathrm{1}}\end{cases}\right. \\ $$
