
Previous in Heat and Theromdynamics Next in Heat and Theromdynamics
Question Number 44298 by Necxx last updated on 26/Sep/18

$$\alpha_{\mathrm{1}} \:{and}\:\alpha_{\mathrm{2}} \:{are}\:{the}\:{temperature} \\ $$$${coefficients}\:{of}\:{the}\:{two}\:{resistors} \\ $$$${R}_{\mathrm{1}} \:{and}\:{R}_{\mathrm{2}} \:{at}\:{any}\:{temperature}\:{T}_{\mathrm{0}} \\ $$$$\mathrm{0}°{C}.{Find}\:{the}\:{equivalent}\:{resistance} \\ $$$${if}\:{both}\:{R}_{\mathrm{1}} \:{and}\:{R}_{\mathrm{2}\:} \:{are}\:{connected}\:{in} \\ $$$${series}\:{combination}.{Assume}\:{that} \\ $$$$\alpha_{\mathrm{1}} \:{and}\:\alpha_{\mathrm{2}} \:{remain}\:{same}\:{with}\:{change} \\ $$$${in}\:{temperature}. \\ $$
Commented by Necxx last updated on 26/Sep/18

$${I}'{ve}\:{tried}\:{this}\:{problem}\:{severally} \\ $$$${but}\:{got}\:{stucked}\:{at}\:{some}\:{point}.{please} \\ $$$${help}.{Thanks}\:{in}\:{advance}. \\ $$
Commented by Necxx last updated on 26/Sep/18

$${please}\:{help} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Sep/18
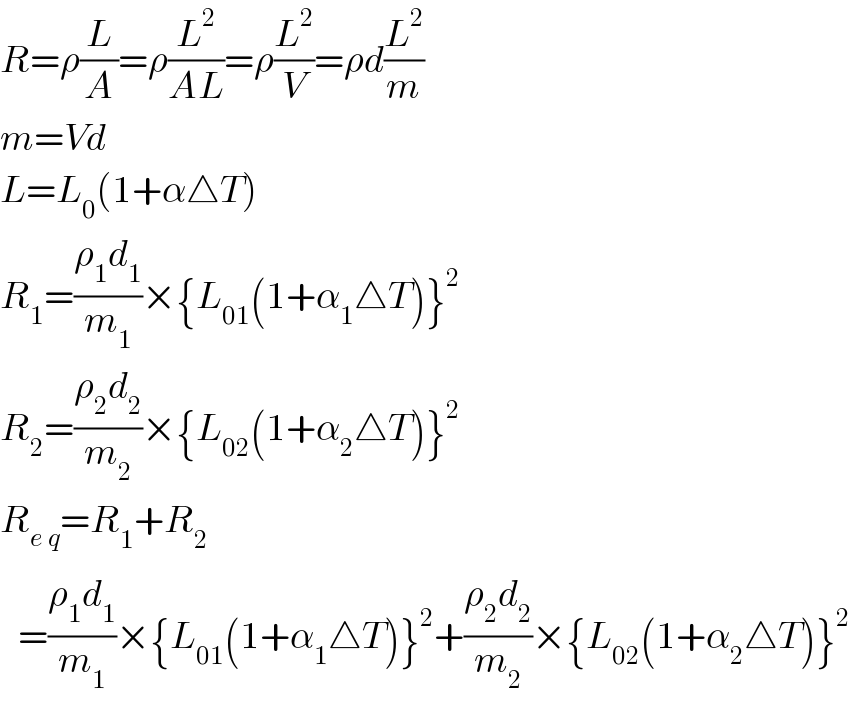
$${R}=\rho\frac{{L}}{{A}}=\rho\frac{{L}^{\mathrm{2}} }{{AL}}=\rho\frac{{L}^{\mathrm{2}} }{{V}}=\rho{d}\frac{{L}^{\mathrm{2}} }{{m}} \\ $$$${m}={Vd} \\ $$$${L}={L}_{\mathrm{0}} \left(\mathrm{1}+\alpha\bigtriangleup{T}\right) \\ $$$${R}_{\mathrm{1}} =\frac{\rho_{\mathrm{1}} {d}_{\mathrm{1}} }{{m}_{\mathrm{1}} }×\left\{{L}_{\mathrm{01}} \left(\mathrm{1}+\alpha_{\mathrm{1}} \bigtriangleup{T}\right)\right\}^{\mathrm{2}} \\ $$$${R}_{\mathrm{2}} =\frac{\rho_{\mathrm{2}} {d}_{\mathrm{2}} }{{m}_{\mathrm{2}} }×\left\{{L}_{\mathrm{02}} \left(\mathrm{1}+\alpha_{\mathrm{2}} \bigtriangleup{T}\right)\right\}^{\mathrm{2}} \\ $$$${R}_{{e}_{} {q}} ={R}_{\mathrm{1}} +{R}_{\mathrm{2}} \\ $$$$\:\:\:=\frac{\rho_{\mathrm{1}} {d}_{\mathrm{1}} }{{m}_{\mathrm{1}} }×\left\{{L}_{\mathrm{01}} \left(\mathrm{1}+\alpha_{\mathrm{1}} \bigtriangleup{T}\right)\right\}^{\mathrm{2}} +\frac{\rho_{\mathrm{2}} {d}_{\mathrm{2}} }{{m}_{\mathrm{2}} }×\left\{{L}_{\mathrm{02}} \left(\mathrm{1}+\alpha_{\mathrm{2}} \bigtriangleup{T}\right)\right\}^{\mathrm{2}} \\ $$
Commented by Necxx last updated on 27/Sep/18
$${wow}....\:{I}\:{love}\:{this}...{Thanks} \\ $$
