
Question Number 5498 by Yozzii last updated on 16/May/16
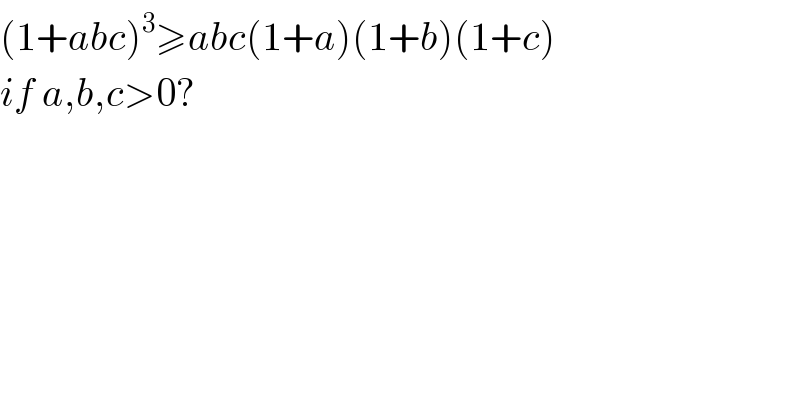
$$\left(\mathrm{1}+{abc}\right)^{\mathrm{3}} \geqslant{abc}\left(\mathrm{1}+{a}\right)\left(\mathrm{1}+{b}\right)\left(\mathrm{1}+{c}\right)\: \\ $$ $${if}\:{a},{b},{c}>\mathrm{0}? \\ $$
Answered by Rasheed Soomro last updated on 17/May/16

Commented byYozzii last updated on 17/May/16
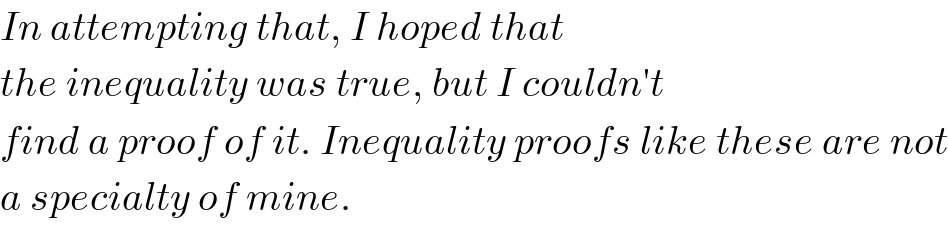
$${In}\:{attempting}\:{that},\:{I}\:{hoped}\:{that}\: \\ $$ $${the}\:{inequality}\:{was}\:{true},\:{but}\:{I}\:{couldn}'{t} \\ $$ $${find}\:{a}\:{proof}\:{of}\:{it}.\:{Inequality}\:{proofs}\:{like}\:{these}\:{are}\:{not} \\ $$ $${a}\:{specialty}\:{of}\:{mine}. \\ $$
Commented byRasheed Soomro last updated on 17/May/16

$$\mathrm{I}\:\mathrm{admit}\:\mathrm{that}\:\mathrm{your}\:\mathrm{comment}\:\mathrm{on}\:\mathrm{Q}#\mathrm{5380},\:\mathrm{in}\:\mathrm{which}\:\mathrm{you}\:\mathrm{reached} \\ $$ $$\mathrm{accidently}\:\mathrm{at}\:\mathrm{the}\:\mathrm{result}\:\mathrm{given}\:\mathrm{in}\:\mathrm{this}\:\mathrm{question}\:\mathrm{and} \\ $$ $$\mathrm{whose}\:\mathrm{screenshot}\:\mathrm{is}\:\mathrm{given}\:\mathrm{here}\left(\mathrm{sorry}\:\mathrm{that}\:\mathrm{I}\:\mathrm{posted}\:\mathrm{it}\:\right. \\ $$ $$\left.\mathrm{without}\:\mathrm{reference}\right)\:\mathrm{is}\:\mathrm{not}\:\mathrm{direct}\:\mathrm{proof}\:\mathrm{of}\:\mathrm{your}\:\mathrm{question} \\ $$ $$\mathrm{but}\:\mathrm{it}\:\:\mathrm{may}\:\mathrm{help}\:\mathrm{to}\:\mathrm{make}\:\mathrm{proof}. \\ $$
