
Question Number 193137 by Mastermind last updated on 04/Jun/23
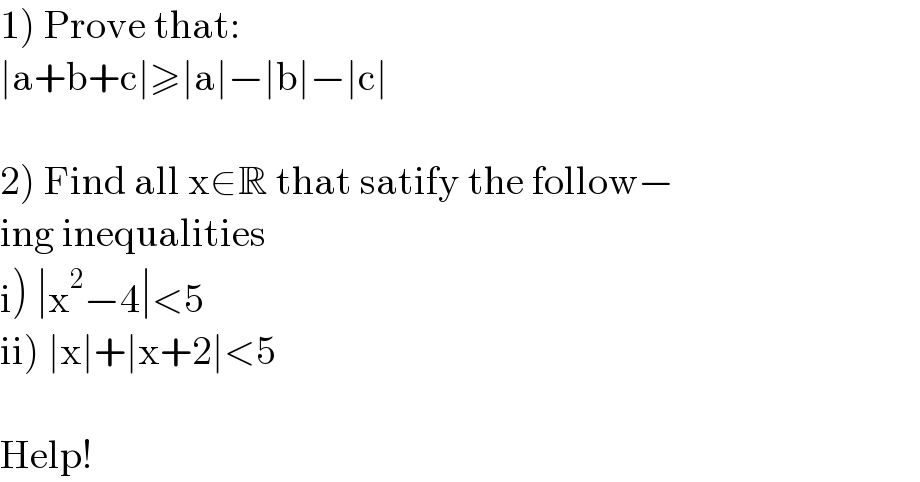
$$\left.\mathrm{1}\right)\:\mathrm{Prove}\:\mathrm{that}: \\ $$$$\mid\mathrm{a}+\mathrm{b}+\mathrm{c}\mid\geqslant\mid\mathrm{a}\mid−\mid\mathrm{b}\mid−\mid\mathrm{c}\mid \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\:\mathrm{Find}\:\mathrm{all}\:\mathrm{x}\in\mathbb{R}\:\mathrm{that}\:\mathrm{satify}\:\mathrm{the}\:\mathrm{follow}− \\ $$$$\mathrm{ing}\:\mathrm{inequalities}\: \\ $$$$\left.\mathrm{i}\right)\:\mid\mathrm{x}^{\mathrm{2}} −\mathrm{4}\mid<\mathrm{5} \\ $$$$\left.\mathrm{ii}\right)\:\mid\mathrm{x}\mid+\mid\mathrm{x}+\mathrm{2}\mid<\mathrm{5} \\ $$$$ \\ $$$$\mathrm{Help}! \\ $$
Answered by aba last updated on 04/Jun/23
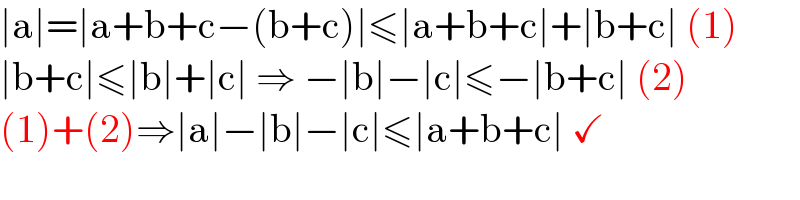
$$\mid\mathrm{a}\mid=\mid\mathrm{a}+\mathrm{b}+\mathrm{c}−\left(\mathrm{b}+\mathrm{c}\right)\mid\leqslant\mid\mathrm{a}+\mathrm{b}+\mathrm{c}\mid+\mid\mathrm{b}+\mathrm{c}\mid\:\left(\mathrm{1}\right) \\ $$$$\mid\mathrm{b}+\mathrm{c}\mid\leqslant\mid\mathrm{b}\mid+\mid\mathrm{c}\mid\:\Rightarrow\:−\mid\mathrm{b}\mid−\mid\mathrm{c}\mid\leqslant−\mid\mathrm{b}+\mathrm{c}\mid\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\Rightarrow\mid\mathrm{a}\mid−\mid\mathrm{b}\mid−\mid\mathrm{c}\mid\leqslant\mid\mathrm{a}+\mathrm{b}+\mathrm{c}\mid\:\checkmark \\ $$
Answered by Rajpurohith last updated on 06/Jun/23

$$\left.\mathrm{1}\right)\mathrm{0}\leqslant\mid{a}\mid=\mid{a}+{b}+{c}−{b}−{c}\mid\leqslant\mid{a}+{b}+{c}\mid+\mid{b}\mid+\mid{c}\mid \\ $$$$\Rightarrow\mid{a}\mid−\mid{b}\mid−\mid{c}\mid\leqslant\mid{a}+{b}+{c}\mid \\ $$$$\left.\mathrm{2}\right) \\ $$$$\left(\mathrm{i}\right){Two}\:{cases}\:{arise}\: \\ $$$$\bullet{x}^{\mathrm{2}} \leqslant\mathrm{4} \\ $$$$\Rightarrow\mid{x}^{\mathrm{2}} −\mathrm{4}\mid=\mathrm{4}−{x}^{\mathrm{2}} <\mathrm{5}\:\Rightarrow−\mathrm{1}\leqslant{x}^{\mathrm{2}} \:{which}\:{is}\:{always}\:{true}. \\ $$$${so}\:{x}^{\mathrm{2}} \leqslant\mathrm{4}\:{is}\:{feasible}\:{i}.{e},\:\mid{x}\mid\leqslant\mathrm{2}. \\ $$$$\bullet{x}^{\mathrm{2}} >\mathrm{4}\:\Rightarrow\mid{x}^{\mathrm{2}} −\mathrm{4}\mid={x}^{\mathrm{2}} −\mathrm{4}<\mathrm{5} \\ $$$$\Rightarrow{x}^{\mathrm{2}} <\mathrm{9}\:\Rightarrow\mid{x}\mid<\mathrm{3} \\ $$$${hence}\:{the}\:{final}\:{region}\:\:{or}\:{solution}\:{is}\:\mid{x}\mid<\mathrm{3}. \\ $$$$ \\ $$$$\left(\mathrm{ii}\right)\:\bullet{Suppose}\:{x}\geqslant\mathrm{0} \\ $$$${then}\:\mid{x}\mid={x}\:{and}\:\mid{x}+\mathrm{2}\mid={x}+\mathrm{2} \\ $$$${so}\:{the}\:{inequality}\:{becomes} \\ $$$${x}+{x}+\mathrm{2}<\mathrm{5} \\ $$$$\Rightarrow\mathrm{2}{x}+\mathrm{2}<\mathrm{5}\Rightarrow{x}<\frac{\mathrm{3}}{\mathrm{2}\:}\:.\:{Hence}\:\mathrm{0}\leqslant{x}<\frac{\mathrm{3}}{\mathrm{2}}\:{is}\:{a}\:{region}. \\ $$$$\bullet{suppose}\:−\mathrm{2}\leqslant{x}<\mathrm{0}\:\Rightarrow{x}+\mathrm{2}\geqslant\mathrm{0} \\ $$$$\Rightarrow\mid{x}\mid=−{x}\:{and}\:\mid{x}+\mathrm{2}\mid={x}+\mathrm{2} \\ $$$${so}\:{the}\:{inequality}\:{becomes}\:−{x}+{x}+\mathrm{2}<\mathrm{5}\:{which}\:{is}\:{true}. \\ $$$${so}\:−\mathrm{2}\leqslant{x}<\mathrm{0}\:\:{is}\:{also}\:{a}\:{feasible}\:{region}. \\ $$$$\bullet{suppose}\:{x}<−\mathrm{2}\:\Rightarrow\mid{x}+\mathrm{2}\mid=−{x}−\mathrm{2}\:{and}\:\mid{x}\mid=−{x} \\ $$$${so}\:{the}\:{inequality}\:{becomes} \\ $$$$−{x}−{x}−\mathrm{2}<\mathrm{5}\:\Rightarrow−\mathrm{2}{x}<\mathrm{7} \\ $$$$\Rightarrow{x}>−\frac{\mathrm{7}}{\mathrm{2}} \\ $$$${hence}\:{the}\:{feasible}\:{region}\:{of}\:{the}\:{inequality}\:{is} \\ $$$$−\frac{\mathrm{7}}{\mathrm{2}}<{x}<\frac{\mathrm{3}}{\mathrm{2}}\:\:. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
