
Question Number 53500 by Otchere Abdullai last updated on 22/Jan/19

$$\mathrm{1}.\:{If}\:\:\sqrt{\left({x}+\mathrm{2}\right)^{\mathrm{2}\:} +{y}^{\mathrm{2}} }+\sqrt{\left({x}−\mathrm{2}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }=\mathrm{6} \\ $$$${show}\:{that}\:{when}\:{the}\:{equation}\:{is}\: \\ $$$${simplified},\:{it}\:{can}\:{be}\:{express}\:{as} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{9}}+\frac{{y}^{\mathrm{2}} }{\mathrm{5}}=\mathrm{1} \\ $$$$\mathrm{2}.\:{find}\:{the}\:{value}\:{of}\:{n}\:{such}\:{that}\:{the} \\ $$$${linear}\:{factors}\:{of}\:{the}\:{form}\:{x}+{ay}+{b}\: \\ $$$${and}\:{x}+{cy}+{d}\:{with}\:{integer}\:{coefficients} \\ $$$${have}\:{the}\:{product}\:{x}^{\mathrm{2}} +\mathrm{5}{xy}+{x}+{ny}−{n} \\ $$$${sir}\:{please}\:{help} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Jan/19
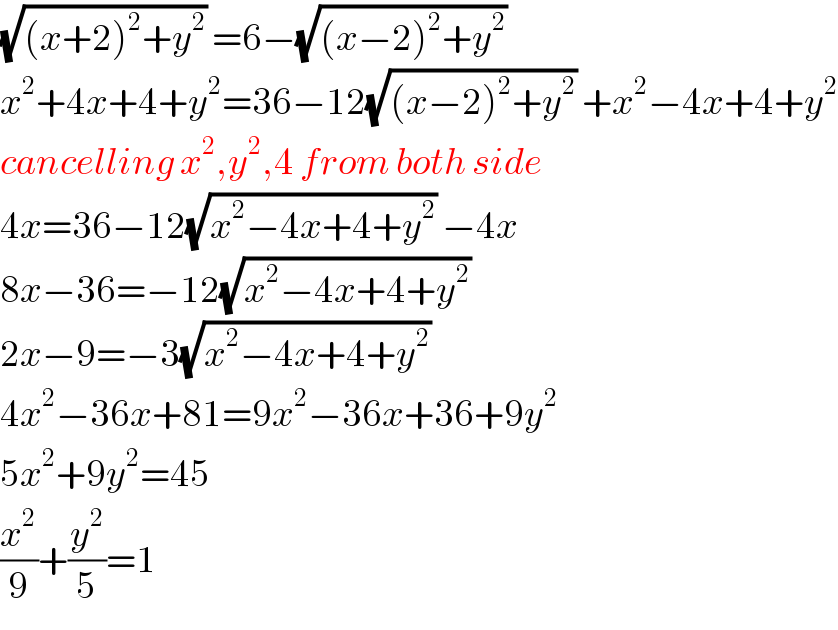
$$\sqrt{\left({x}+\mathrm{2}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }\:=\mathrm{6}−\sqrt{\left({x}−\mathrm{2}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }\: \\ $$$${x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}+{y}^{\mathrm{2}} =\mathrm{36}−\mathrm{12}\sqrt{\left({x}−\mathrm{2}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }\:+{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}+{y}^{\mathrm{2}} \\ $$$${cancelling}\:{x}^{\mathrm{2}} ,{y}^{\mathrm{2}} ,\mathrm{4}\:{from}\:{both}\:{side} \\ $$$$\mathrm{4}{x}=\mathrm{36}−\mathrm{12}\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}+{y}^{\mathrm{2}} }\:−\mathrm{4}{x} \\ $$$$\mathrm{8}{x}−\mathrm{36}=−\mathrm{12}\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}+{y}^{\mathrm{2}} }\: \\ $$$$\mathrm{2}{x}−\mathrm{9}=−\mathrm{3}\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}+{y}^{\mathrm{2}} }\: \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{36}{x}+\mathrm{81}=\mathrm{9}{x}^{\mathrm{2}} −\mathrm{36}{x}+\mathrm{36}+\mathrm{9}{y}^{\mathrm{2}} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} +\mathrm{9}{y}^{\mathrm{2}} =\mathrm{45} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{9}}+\frac{{y}^{\mathrm{2}} }{\mathrm{5}}=\mathrm{1} \\ $$
Commented by Otchere Abdullai last updated on 22/Jan/19
$${wow}!\:{thank}\:{you}\:{sir}\:{God}\:{bless}\:{you} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Jan/19
![2)(x+ay+b)(x+cy+d)=x^2 +5xy+x+ny−n x^2 +cxy+xd+axy+acy^2 +ayd+bx+bcy+bd=x^2 +5xy+x+ny−n x^2 +xy(a+c)+x(b+d)+y(ad+bc)+acy^2 +bd=x^2 +5xy+x+ny−n so a+c=5 b+d=1 ad+bc=n ac=0 bd=−n ac=0 a(5−a)=0 either a=0 or a=5 when a=0 c=5 and when a=5 c=0 now let a=0 c.=5 ad+bc=n 0×d+b×5=n [b=(n/5)] a=0 b=(n/5) c=5 d=1−b=1−(n/5) bd=−n ((n/5))×(1−(n/5))=−n (1/5)×(((5−n)/5))=−1 5−n=−25 −n=−30 ...n=30](Q53508.png)
$$\left.\mathrm{2}\right)\left({x}+{ay}+{b}\right)\left({x}+{cy}+{d}\right)={x}^{\mathrm{2}} +\mathrm{5}{xy}+{x}+{ny}−{n} \\ $$$${x}^{\mathrm{2}} +{cxy}+{xd}+{axy}+{acy}^{\mathrm{2}} +{ayd}+{bx}+{bcy}+{bd}={x}^{\mathrm{2}} +\mathrm{5}{xy}+{x}+{ny}−{n} \\ $$$${x}^{\mathrm{2}} +{xy}\left({a}+{c}\right)+{x}\left({b}+{d}\right)+{y}\left({ad}+{bc}\right)+{acy}^{\mathrm{2}} +{bd}={x}^{\mathrm{2}} +\mathrm{5}{xy}+{x}+{ny}−{n} \\ $$$${so} \\ $$$${a}+{c}=\mathrm{5} \\ $$$${b}+{d}=\mathrm{1} \\ $$$${ad}+{bc}={n} \\ $$$${ac}=\mathrm{0} \\ $$$${bd}=−{n} \\ $$$${ac}=\mathrm{0} \\ $$$${a}\left(\mathrm{5}−{a}\right)=\mathrm{0}\:\:\:{either}\:{a}=\mathrm{0}\:{or}\:{a}=\mathrm{5} \\ $$$${when}\:\:{a}=\mathrm{0}\:\:{c}=\mathrm{5}\:\:{and}\:{when}\:{a}=\mathrm{5}\:\:{c}=\mathrm{0} \\ $$$${now}\:{let}\:{a}=\mathrm{0}\:\:{c}.=\mathrm{5} \\ $$$${ad}+{bc}={n} \\ $$$$\mathrm{0}×{d}+{b}×\mathrm{5}={n}\:\:\:\left[{b}=\frac{{n}}{\mathrm{5}}\right] \\ $$$${a}=\mathrm{0} \\ $$$${b}=\frac{{n}}{\mathrm{5}} \\ $$$${c}=\mathrm{5} \\ $$$${d}=\mathrm{1}−{b}=\mathrm{1}−\frac{{n}}{\mathrm{5}} \\ $$$${bd}=−{n} \\ $$$$\left(\frac{{n}}{\mathrm{5}}\right)×\left(\mathrm{1}−\frac{{n}}{\mathrm{5}}\right)=−{n} \\ $$$$\frac{\mathrm{1}}{\mathrm{5}}×\left(\frac{\mathrm{5}−{n}}{\mathrm{5}}\right)=−\mathrm{1} \\ $$$$\mathrm{5}−{n}=−\mathrm{25} \\ $$$$−{n}=−\mathrm{30}\:...{n}=\mathrm{30} \\ $$$$ \\ $$
Commented by Otchere Abdullai last updated on 22/Jan/19

$${powerful}\:\:{Mathematician}!\:{We}\:{thank} \\ $$$${God}\:{for}\:{having}\:{you}\:{in}\:{the}\:{group} \\ $$$${God}\:{bless}\:{you}\:{sir}! \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 22/Jan/19
$${mathematics}...{activates}\:{ones}\:{mind}\:{to}\:{think}... \\ $$
