Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 211603 by MrGaster last updated on 14/Sep/24

1.Given a regular tetrahedron ABCD with vertices A(0,0,0)B(a,0,0), C(0,a,0),and D(0,0,a).Calculate the volume V and the surface area S of this tetrahedron.

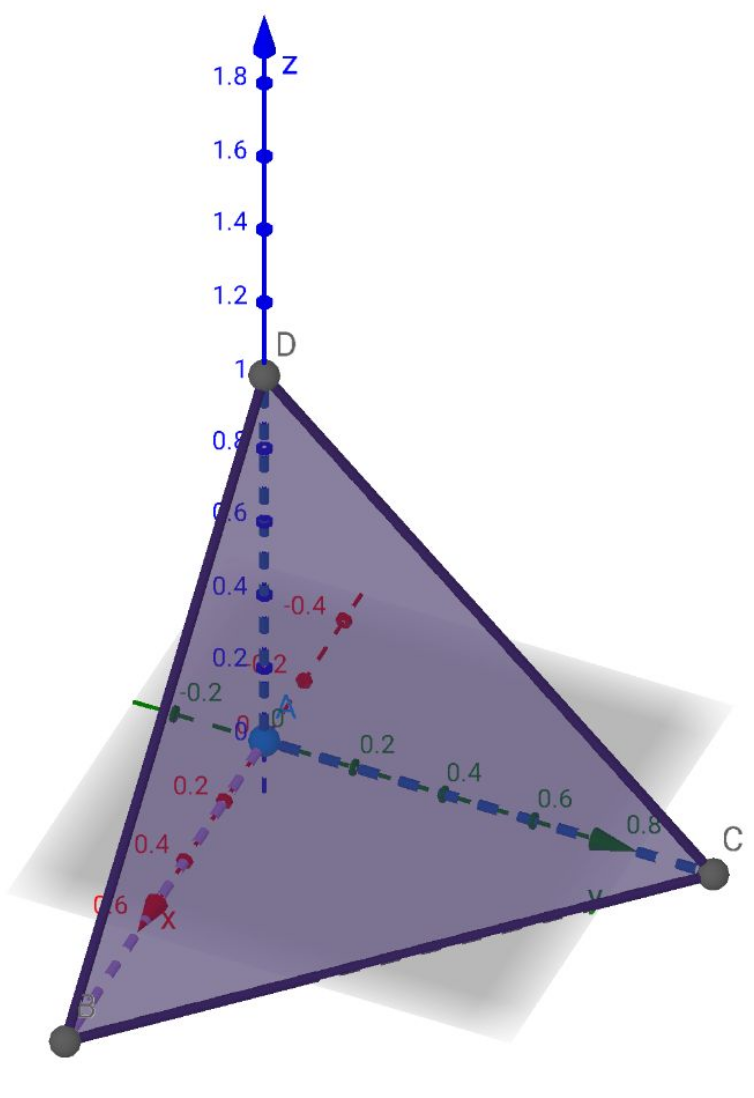
$$\mathrm{1}.\mathrm{Given}\:\mathrm{a}\:\mathrm{regular}\:\mathrm{tetrahedron}\:\boldsymbol{{ABCD}} \\ $$$$\mathrm{with}\:\mathrm{vertices}\:\boldsymbol{{A}}\left(\mathrm{0},\mathrm{0},\mathrm{0}\right)\boldsymbol{{B}}\left(\boldsymbol{{a}},\mathrm{0},\mathrm{0}\right), \\ $$$$\boldsymbol{{C}}\left(\mathrm{0},\boldsymbol{{a}},\mathrm{0}\right),\boldsymbol{\mathrm{and}}\:\boldsymbol{{D}}\left(\mathrm{0},\mathrm{0},\boldsymbol{{a}}\right).\mathrm{Calculate}\:\mathrm{the} \\ $$$$\:\mathrm{volume}\:\boldsymbol{{V}}\:\:\mathrm{and}\:\mathrm{the}\:\mathrm{surface}\:\mathrm{area}\:\boldsymbol{{S}}\:\boldsymbol{\mathrm{of}} \\ $$$$\mathrm{this}\:\mathrm{tetrahedron}. \\ $$

Answered by BHOOPENDRA last updated on 14/Sep/24

Answered by BHOOPENDRA last updated on 15/Sep/24

The volume of a tetrahedron with vertices A,B,C,&D is given formula V=(1/6)∣A.(B×C)∣ A(0,0,0) ,B(a,0,0) ,C(0,a,0)D(0,0,a) V=(1/6) determinant (((0 0 0 )),((a 0 0 )),((0 a 0)),((0 0 a)))=(1/6)∣a^3 ∣ V=(1/6)a^3 Surface area =(3×area right angle triangle)+equiletral triangle area =3×(1/2)a^2 +((√3)/4) ((√2) a)^2 = (((3+(√3))a^2 )/( 2))

$${The}\:{volume}\:{of}\:{a}\:{tetrahedron}\:{with}\: \\ $$$${vertices}\:{A},{B},{C},\&{D}\:{is}\:{given}\:{formula} \\ $$$${V}=\frac{\mathrm{1}}{\mathrm{6}}\mid{A}.\left({B}×{C}\right)\mid \\ $$$${A}\left(\mathrm{0},\mathrm{0},\mathrm{0}\right)\:,{B}\left({a},\mathrm{0},\mathrm{0}\right)\:,{C}\left(\mathrm{0},{a},\mathrm{0}\right){D}\left(\mathrm{0},\mathrm{0},{a}\right) \\ $$$$ \\ $$$${V}=\frac{\mathrm{1}}{\mathrm{6}}\begin{vmatrix}{\mathrm{0}\:\:\mathrm{0}\:\:\:\mathrm{0}\:}\\{{a}\:\:\mathrm{0}\:\:\:\mathrm{0}\:\:\:}\\{\mathrm{0}\:\:\:{a}\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\mathrm{0}\:\:\:{a}}\end{vmatrix}=\frac{\mathrm{1}}{\mathrm{6}}\mid{a}^{\mathrm{3}} \mid \\ $$$${V}=\frac{\mathrm{1}}{\mathrm{6}}{a}^{\mathrm{3}} \\ $$$${Surface}\:{area}\:=\left(\mathrm{3}×{area}\:{right}\:{angle}\:{triangle}\right)+{equiletral}\:{triangle}\:{area} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3}×\frac{\mathrm{1}}{\mathrm{2}}{a}^{\mathrm{2}} +\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\:\left(\sqrt{\mathrm{2}}\:{a}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\left(\mathrm{3}+\sqrt{\mathrm{3}}\right){a}^{\mathrm{2}} }{\:\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Commented by BHOOPENDRA last updated on 14/Sep/24

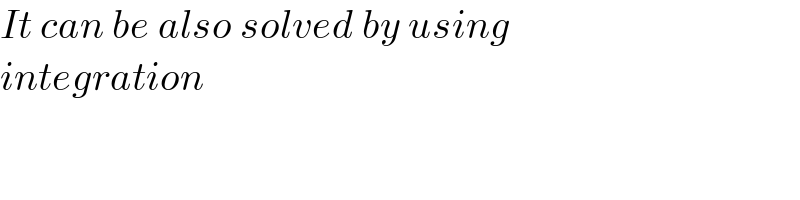
It can be also solved by using integration

$${It}\:{can}\:{be}\:{also}\:{solved}\:{by}\:{using}\: \\ $$$${integration} \\ $$

Answered by mr W last updated on 15/Sep/24

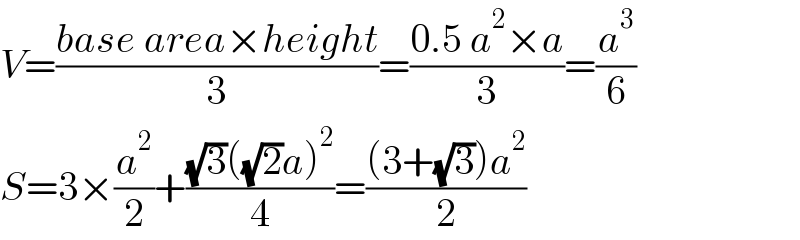
V=((base area×height)/3)=((0.5 a^2 ×a)/3)=(a^3 /6) S=3×(a^2 /2)+(((√3)((√2)a)^2 )/4)=(((3+(√3))a^2 )/2)

$${V}=\frac{{base}\:{area}×{height}}{\mathrm{3}}=\frac{\mathrm{0}.\mathrm{5}\:{a}^{\mathrm{2}} ×{a}}{\mathrm{3}}=\frac{{a}^{\mathrm{3}} }{\mathrm{6}} \\ $$$${S}=\mathrm{3}×\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{2}}{a}\right)^{\mathrm{2}} }{\mathrm{4}}=\frac{\left(\mathrm{3}+\sqrt{\mathrm{3}}\right){a}^{\mathrm{2}} }{\mathrm{2}} \\ $$

Commented by BHOOPENDRA last updated on 15/Sep/24

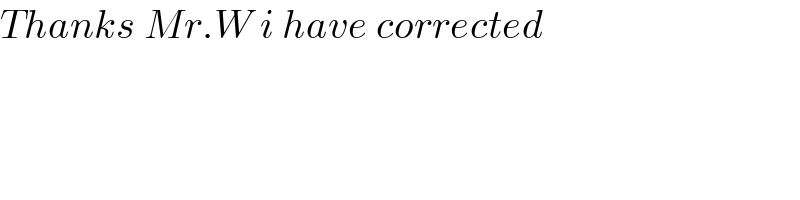
Thanks Mr.W i have corrected

$${Thanks}\:{Mr}.{W}\:{i}\:{have}\:{corrected}\: \\ $$

Commented by mr W last updated on 15/Sep/24

��

Terms of Service

Privacy Policy

Contact: info@tinkutara.com